The Most Beautiful Equation of Math: Euler’s Identity
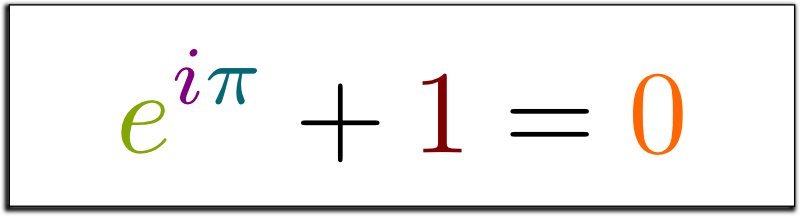
In 1988, Euler’s identity was elected most beautiful theorem of mathematics. It has been widely taught worldwide. But have you ever stopped to really sense the meaning of this incredible formula? This article does.
The Amazing Physics of Water in Trees

As explained by Derek Muller on Veritasium, the flow of water in trees involves complex physical phenomena including pressure, osmosis, negative pressure, capillarity and evapotranspiration. What seems simple will blow your mind!
The Beauty of Ellipses, Parabolas and Hyperbolas

The conic sections, that is, ellipses, parabolas and hyperbolas, are too often presented analytically. Yet, their amazing beauty is actually their spectacular geometry, as well as their omnipresence! This article presents plenty of illustrative descriptions of their uncountable applications!
Shannon’s Information Theory

Claude Shannon may be considered one of the most influential person of the 20th Century, as he laid out the foundation of the revolutionary information theory. Yet, unfortunately, he is virtually unknown to the public. This article is a tribute to him. And the best way I’ve found is to explain some of the brilliant ideas he had.
The Addictive Mathematics of the 2048 Tile Game

2048 is the Internet sensation of the year. This very addictive game has been downloaded hundred of millions of times. Interestingly, this game raises plenty of intriguing mathematical questions. This article unveils some of them!
Entropy and the Second Law of Thermodynamics
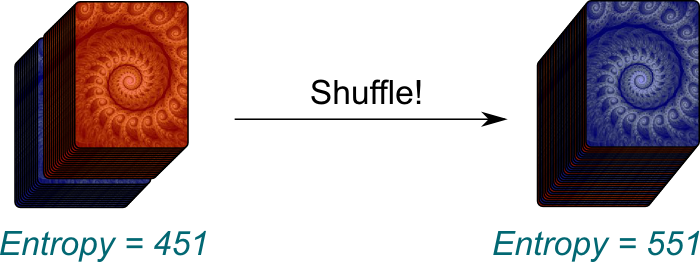
The second law of thermodynamics is my favorite law in physics, mainly because of the troubling puzzles it raises! Indeed, what your professors may have forgotten to tell you is that this law connects today’s world to its first instant, the Big Bang! Find out why!
Primal and Dual Simplex Methods
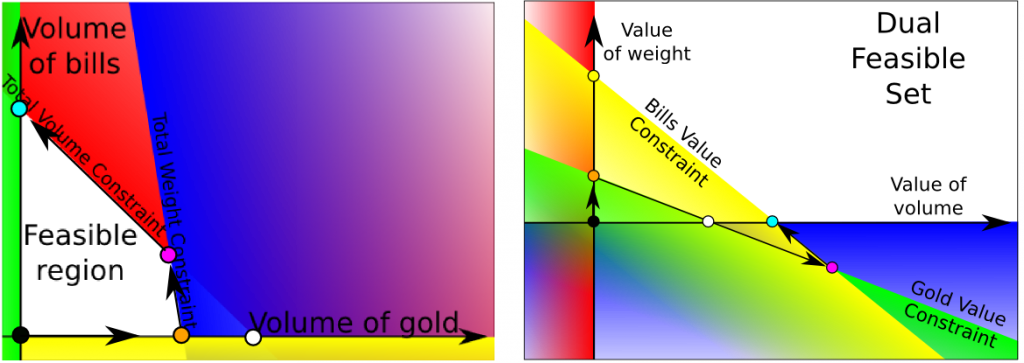
The simplex method is one of the major algorithm of the 20th century, as it enables the resolution of linear problems with millions of variables. An intuitive approach is given. But that’s not all. We present an important variant called the dual simplex. Finally, we’ll explain its main default, that is, when facing degeneracy.
Duality in Linear Programming
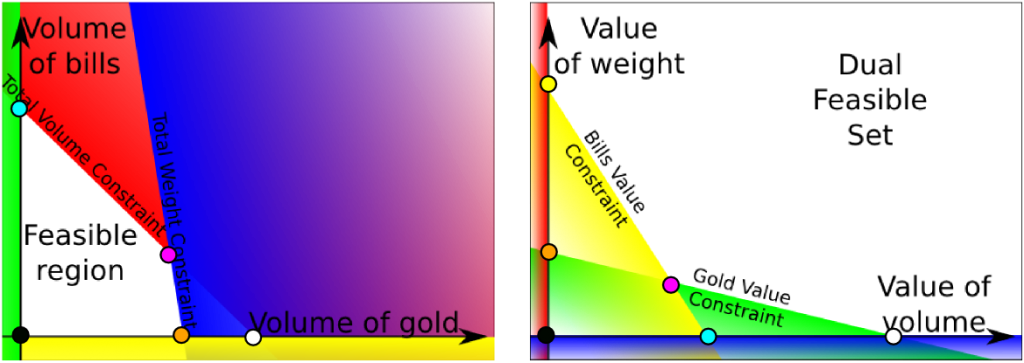
Duality in linear programming yields plenty of amazing results that help understand and improve algorithms of resolution. This article shows the construction of the dual and its interpretation, as well as major results. In particular, matching of primal and dual bases will be dealt, before presenting the issue of degeneracy and its dual interpretation.
The Revolutionary Galois Theory

In 1832, Évariste Galois died. He was 20. The night before his death, he wrote a legendary letter to his friend, in which he claims to have found a mathematical treasure! Sadly, this treasure had long been buried in total indifference! It took nearly a century to rediscover it! Since then, Galois’ legacy has become some of the finest pure mathematics, which represents a hugely active field of research today with crucial applications to cryptography. Galois’ work is now known as Galois theory. In essence, it unveils the hidden symmetries of numbers!
The Tortuous Geometry of the Flat Torus

Take a square sheet of paper. Can you glue opposite sides without ever folding the paper? This is a conundrum that many of the greatest modern mathematicians, like Gauss, Riemann, and Mandelbrot, couldn’t figure out. While John Nash did answer yes, he couldn’t say how. After 160 years of research, Vincent Borrelli and his collaborators have finally provided a revolutionary and breathtaking example of a bending of a square sheet of paper! And it is spectacularly beautiful!
All Other Articles…
Euler’s Formula and the Utilities Problem
Darwin’s Theory of Evolution
Spacetime of General Relativity
Fourier Analysis: Signals and Frequencies
Game Theory and the Nash Equilibrium
The Essence of Quantum Mechanics
Non-Euclidean Geometry and Map-Making
The Cubic Ball of the 2014 FIFA World Cup
Numbers and Constructibility
Poincaré Conjecture and Homotopy
Optimization by Integer Programming
Homotopy Type Theory and Higher Inductive Types
Topology: from the Basics to Connectedness
Differential Calculus and the Geometry of Derivatives
A Model of Football Games
Linear Algebra and Higher Dimensions
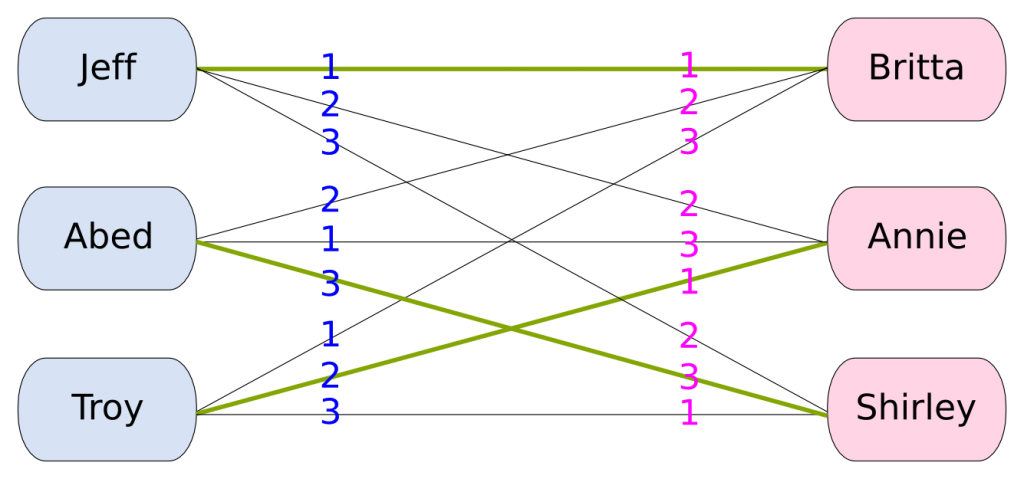
Marriage Assignment Problem and Variants
HDI: a measure of human capabilities
Proof by Mathematical Induction
Fair Division and Cake-Cutting
Evolutionary Game Theory
Symmetries and Group Theory
Conditional Probabilities: Know what you Learn
Colours and Dimensions
Dynamics, Chaos, Fractals (pt 1)
The Biology Civil War Opposing Kin to Group Selection
Univalent Foundations of Mathematics
The Limitless Vertigo of Cantor’s Infinite
The Magic of Algebra
Spacetime of Special Relativity
Can we measure peace ? The Global Peace Index (GPI)
Temperature Misconception: Heat is Not How it Feels
Cryptography and Quantum Physics
The Most Troubling Experiments on Human Behavior
The Frontier of Cold: The Quest for Absolute Zero
Probabilistic Algorithms, Probably Better
The Magic of Analysis
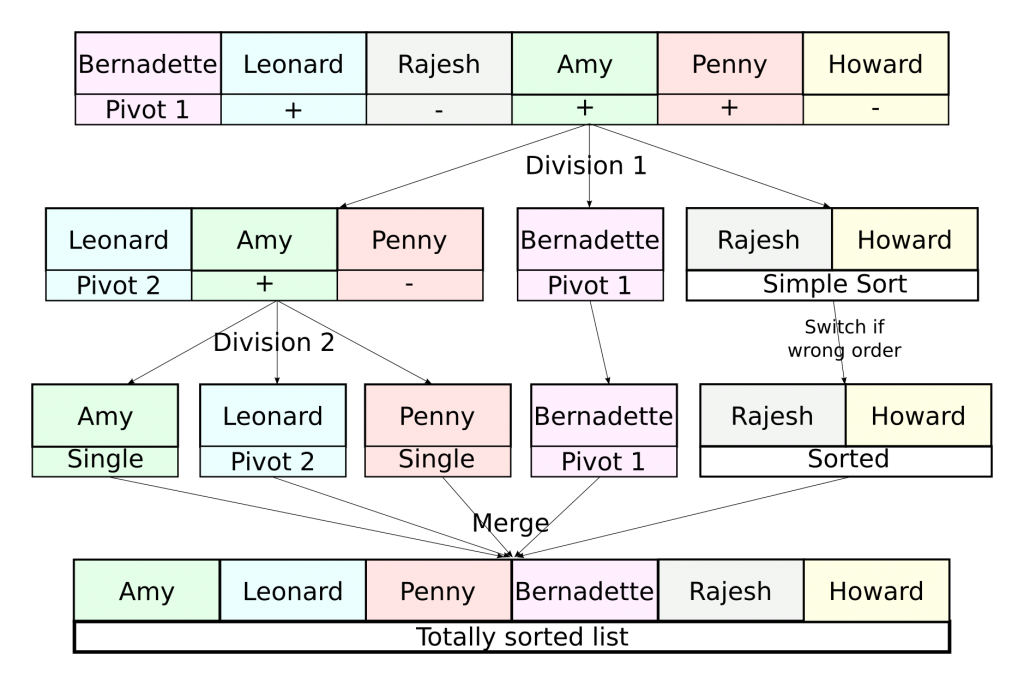
From Divide and Conquer to Parallelization
Glaciers: Retreat, Moraines, Valleys, Fjörds
The coach’s dilemma.
Computing Hunger worldwide: the Global Hunger Index (GHI)
The New Big Fish Called Mean-Field Game Theory
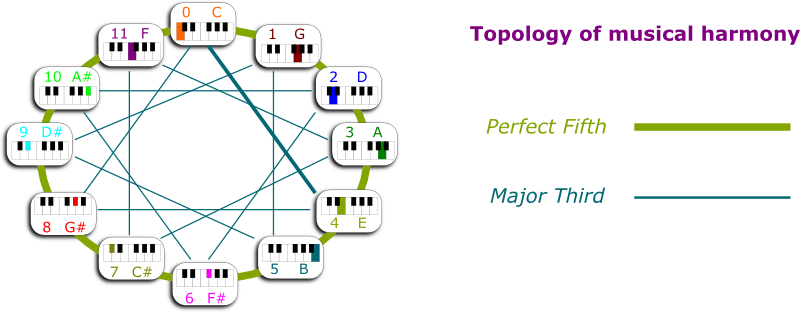
The Harmonious Mathematics of Music
Column Generation and Dantzig-Wolfe Decomposition
Type Theory: A Modern Computable Paradigm for Math
The Triangle of Power
The Surprising Flavor of Infinite Series
Dynamics of the Wave Function: Heisenberg, Schrödinger, Collapse
The Unlikely Correctness of Newton’s Laws
Construction and Definition of Numbers
Logarithms and Age Counting
Euclidean Geometry and Navigation
Santa Routing and Heuristics in Operations Research
Bayesian Games: Math Models for Poker
Optimization by Linear Programming
Colors: It’s not just about Wavelengths!
P versus NP: A Crucial Open Problem
Mechanism Design and the Revelation Principle
Imaginary and Complex Numbers
Self-Reference, Math Foundations and Gödel’s Incompleteness
Advanced Game Theory Overview
The Secretary/Toilet Problem and Online Optimization
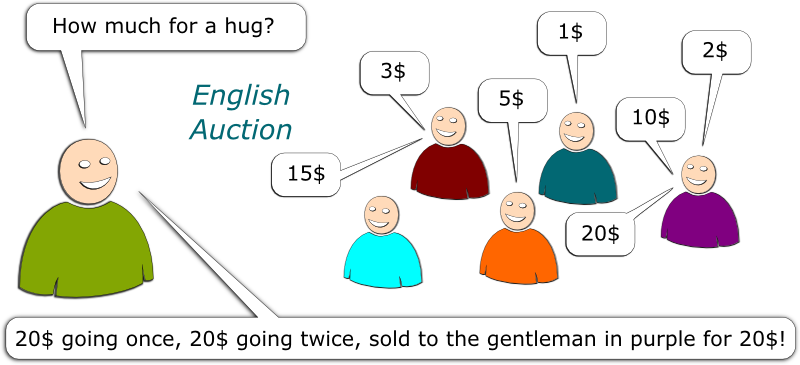
A Mathematical Guide to Selling
From Britain’s coast to Julia set: an introduction to fractals
Model-Dependent Realism
Hypothesis Test with Statistics: Get it Right!
The Massive Puzzles of Gravity
Web Programming: From HTML to AJAX
High Dynamic Range and Tone Mapping
Geometry and General Relativity
Pluto is NOT (not?) a Planet
The forces of Nature: from Newton to String Theory
Multicriteria with MACBETH
Space Deformation and Group Representation
Geological Wonders of Iceland
Dynamics, Chaos, Fractals (pt 2)
Regulation of Electricity Markets
Beauty, the Driving Force of our Quest for Truth
Does God play dice?
Dual Variable Stabilization
What Makes a Published Result Believable?