This article follows my article on the essence of quantum mechanics, where I pointed out that everything is made of elementary waves. This is a big assumption of quantum mechanics, which then describes how these waves behave through time. This dynamics of wave functions is what will be discussed here. We will be using visualizations of my own creation based on the mathematics of quantum mechanics.
The Wave Function
Recall that these waves are fields which map each point of space with a number. This number is called the amplitude of the wave at that point. To simplify our understanding of wave functions, let’s consider a 1-dimension space. In this setting, waves are commonly represented as signals through space, as follows.
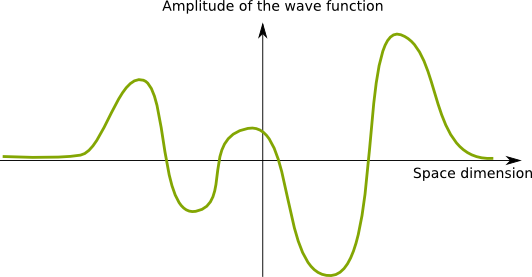
Now, the figure above represents a real-valued field. But the amplitude of the wave function is rather a complex number.
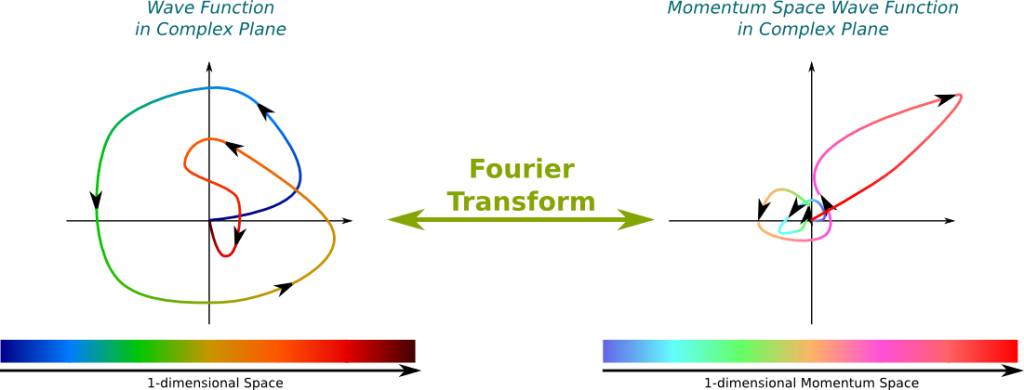
It’s not wrong. But it’s incomplete. Thus, let me introduce a new visualization of wave functions of my own creation. In this setting, each color corresponds to a position in space. Then, the amplitude of the wave function at a position in space is represented by its associated dot in the complex plane. This dot is colored by the color associated to the position in space. The wave can then be seen as a colored path in the complex plane.
For instance, the amplitude of the wave function drawn above at the green position in space is -1, that is, the point of distance 1 from the origin on its left. Since this point is one of the farthest for the origin, the square of the norm of the amplitude is relatively great. This means that the green position is one of the most likely position where the wave may collapse to if observed.
Good question. Let’s assume that the wave function has collapsed around the green position. This means that the wave function is very localized around this position, and nearly nil anywhere else. Then, we’d obtain the following figure:
No! Wave functions are defined up to a phase. This means that a rotation of the complex plane change nothing to the physical nature of the wave. So a vertical localized wave would be essentially identical to the one above!
Momentum Space Wave Function
So far, we have described the position of the particle. In classical physics, we’d only need to know about its velocity to know everything about it. Equivalently, we can focus on its momentum. Classically, the momentum is the velocity multiplied by the mass of the particle. It’s a much more significative concept in physics because of the law of conservation of momentum, which states that the momentum of a closed system is always conserved. This has been essential to explain the photoelectric effect, which boils down to a transfer of momentum from photons to electrons.
What Planck and Einstein showed is that the momentum of light depends on the frequency of its wave and its direction of motion. What we usually mean by frequency of light is the time frequency of the wave, but since the speed of light is constant, we may equivalently consider the spatial frequency, also known as the wavenumber. A similar definition occurs in quantum physics for all particles.
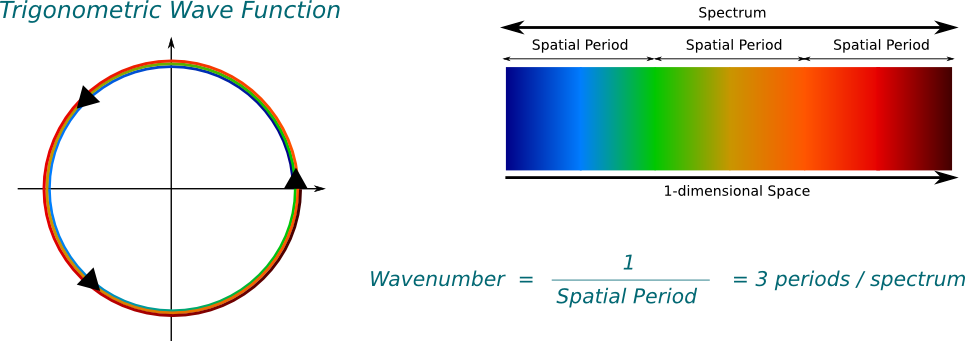
Basically, yes! Now, we have to be a little more careful before actually talking about frequencies. The basis of all frequencies comes from trigonometric waves. In the complex plane, the trigonometric waves are the simplest periodic paths one can think of: Circles. In this setting, the wavenumber corresponds to the number of cycles of the trigonometric wave in 1 meter. Equivalently, it is the inverse of the spatial period, as displayed below.
Note that the trigonometric function in the figure turns anti-clockwise. This is important. It implies that the wavenumber of the trigonometric wave is positive, and that the associated wave function goes from left to right. If it went clockwise, it would be negative.
No, because they don’t start nor end at 0. This is incompatible with waves representing probabilities.
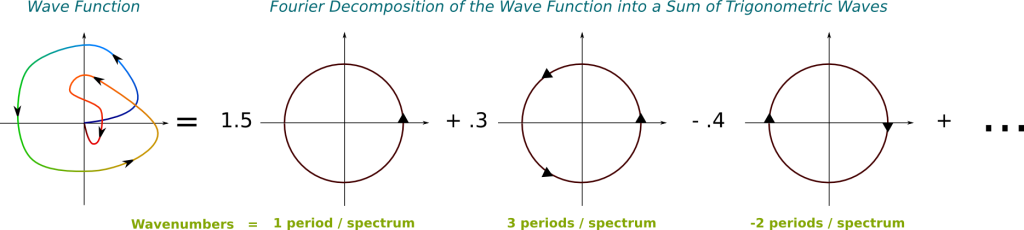
We need to use the Fourier analysis. According to this, any wave is uniquely decomposable into an infinite superposition of trigonometric waves of different frequencies. This means that, for any wave and any frequency, the wave is composed of a certain amount of the trigonometric wave of that frequency. And the decomposition is given by the Fourier transform. Basically, the Fourier transform provides a description of any wave, like the one on the left, by an infinite combination of trigonometric waves, like those on the right:
In this figure, the greater the wavenumber, the more arrows I have put on the trigonometric functions. Note that the greater the wavenumber, the more energy is associated to it.
The Fourier transform takes the wave function as an input and returns the weights of trigonometric waves on the right. Note that these weights can actually take complex numbers. In fact, by considering that the weight of trigonometric waves which don’t appear on the right is 0, we can consider this output as a matching of every wavenumber with an amplitude.
The momentum is proportional to the wavenumber! This corresponds to the relation $p=hk/(2\pi)$, where $p$ is the momentum, $h$ is the Planck constant and $k$ is the wavenumber. From the Fourier transform that provides a mapping of every wavenumber with an amplitude, we can easily deduce a mapping of every momentum with an amplitude. We call this matching the momentum space wave function. By opposition, the wave function is sometimes called the position space wave function.
Precisely! A wave function has a superposition of momenta! And the fact that there are several momenta associated to a wave functions shouldn’t be the only thing shocking you, especially if you’re familiar with classical mechanics.
Classically, the position and the momentum of a particle are two distinct concepts which can be defined independently from each other. But it’s not the case in quantum mechanics! Now, the position of a wave function is distributed in space. Weirdly enough, the mere knowledge of the amplitudes of positions determine the amplitudes of momenta! The reciprocal phrase is true too: The amplitudes of momenta determine the amplitudes of positions. Mathematically, this corresponds to saying that the Fourier transform is more or less a bijection from the Hilbert space of wave functions and the Hilbert space of momentum space wave functions.
This mapping of wave functions with momentum space wave functions by the Fourier transform is displayed below. The following figure is definitely false since I haven’t made any actual computation to draw this. It rather aims at providing you an image of what the intimate relationship between position space and momentum space wave functions.
Heisenberg’s Principle
Yes! The square of the norm of the value of the momentum space wave function is the probability density function of finding the momenta in case of observation.
This is what’s called Heisenberg’s uncertainty principle. But I believe that the word uncertainty is misleading. Rather, you should think of Heisenberg’s principle as a spreading principle.
It says that the wave function and the momentum space wave function can’t be both localized. This is a direct consequence of their relationship through the Fourier transform. For instance, in the case of the figure above, where the momentum space wave function was localized around the pink-red momentum, while the wave function was spread all over the spectrum.
Imagine that the momentum space wave function were perfectly localized at one momentum. Recall that the wave function is obtained by summing all momentum space wave functions of all momenta. This implies that the wave function is nearly the trigonometric wave associated to the momentum at which the momentum space wave function is localized. This trigonometric wave circles over all space, and is therefore spread over all space. This is represented below:
Conversely, were the wave function very localized, the momentum space wave function would be circling periodically, and would therefore be spread over all momentum space.
Technically, the spreading of a wave function is measured by the standard deviation of the probabilistic distribution of position induced by the wave function. Now, I have been using the word probabilistic, but you don’t need to mention probability to describe the spreading of the wave function. Indeed, the mathematical concept matches the intuitive idea of how far in space the wave is spread.
It states that the product of the spreading of the wave function by the spreading of the momentum space wave function must be greater than $h/(4\pi)$.
This is because people often focus on the measurement part of quantum mechanics. In this setting, what’s surprising is that the measurement of the position of a wave localizes the wave around a position. As a result, the wave function becomes very localized, which implies that the momentum space wave function is greatly spread. As quantum mechanics was approached with concepts of classical mechanics, this frustrating phenomenon was commented as the impossibility of knowing both position and momentum simultaneously. But quantum mechanics rather says that when the wave is very localized, then the wave has a superposition of a large range of momenta. This principle doesn’t involve any probability.
Yes! This has been done by Derek Muller on Veritasium in a very simple experiment! Check out this awesome video:
Schrödinger Equation
Yes! The momentum is still somehow the velocity of a particle multiplied by its mass. And the reason why such a reasoning holds is because of the most fundamental equation of quantum physics which describes the dynamics of wave functions. This equation is the Schrödinger equation.
Hummm… That’s a tough one. I have a lot of trouble making sense out of it. Here’s the best explanation I’ve come up with. At any position of space, a wave function has a particular energy which is deduced from its global structure. This local energy, also known as the Hamiltonian, is a composition of some potential energy which is due to external forces like electromagnetism, and some kinetic energy which depends on the superposition of momenta which makes up the wave function. What’s particularly weird about this kinetic energy is that it can have a complex value. Now, what Schrödinger equation says is that, at every position, the wave function rotates around the origin of the complex plane at a speed proportional to the Hamiltonian. This corresponds to the following formula:
From Schrödinger equation can be derived the fact that the average position varies according to the average momentum. This coincides with the classical setting of classical mechanics! This should sound surprising to you. At least, it does to me. Even though I can prove it mathematically, I have no understanding of the fundamental reason why Schrödinger equation links average position and average momentum.
Sorry for that. But anyways, the greatest applications of Schrödinger equation rather concern the calculations of stationary states. Indeed, at the scale we are looking at, distances are so short that stationary states are reached in such a small fraction of time that we can only observe these equilibria.
It’s a wave function which will appear to be non-moving. Now, recall that the wave function is defined up to a rotation in the complex plane. Thus, stationary states involve only such rotations. The following figure shows a wave function rotating. Arrows drawn on the wave represent the velocity at which each point of the wave moves:
Now, for a wave to be stationary, the velocity at any given point must be perpendicular to the vector from the origin to that point. Also, the farther to the origin a point is, the greater the speed must be. These two conditions correspond to the Hamiltonian at position being proportional to the wave function at this position with a real-valued proportionality coefficient independent from this position. In mathematical terms, this means that the wave function should be an eigenvector of the Hamiltonian. The eigenvalue, which is the real proportionality coefficient, is then the energy of the wave. This corresponds to what’s known as the time-independent Schrödinger equation:
Exactly! The faster the wave turns, the greater the energy. More precisely the energy of the wave is the number of turns it makes in a second multiplied by Planck’s constant. In other words, Planck’s constant is the energy of a wave which turns at the speed of 1 turn per second. Since rotational speed is often rather measured in radians per second, physicists often prefer to use reduced Planck’s constant $\hbar$, which is therefore $\hbar = h/(2\pi)$.
Yes! As it turns out, in any defined system, not all energies can be reached by a stationary wave. The set of all possible energies, which is called the spectrum of the Hamiltonian, is made of discrete values more often than not. In particular, this is what happens if we consider wave functions confined in a box.
No indeed. More interestingly, in an atom, the positive charges of a nucleus affect the potential energies of wave functions of electrons, which in turns modify the Hamiltonian. The eigenvalues and eigenvectors of the obtained Hamiltonian, especially the lowest eigenvalues, now correspond to possible orbits of electrons around the nucleus. The lower energies refer to stationary wave functions localized closer to the nucleus. This phenomenon accounts for Niels Bohr’s weird model of the hydrogen atom, as explained in this video from the Science Channel:
Fortunately, no. Because of Pauli’s exclusion principle, two electrons cannot be in the same quantum state. A quantum state is defined by the wave function and the spin of the electron, which can be up or down. Since there are only two spins, this means that there are at most two electrons with the same wave function. In particular, the energy levels cannot contain too many electrons, which implies that there are sorts of blanks around nuclei that can each contain one electron only.
Without Pauli’s exclusion principle, electrons would not be able to combine atoms together, which means that there would be no chemistry. No chemistry, no life. No life, none of us…
Collapse
If you look carefully at what we’ve discussed until now, no probability is involved. Indeed, Schrödinger equation is perfectly deterministic and time-revertible.
Half of quantum mechanics has absolutely nothing to do with probabilities. And this half accounts for plenty of counter-intuitive observations. But there are other observations which can’t be explained without the other half of quantum mechanics. This is the case, for instance, of the troubling double slit experiment and its variants you can read about in my article introducing quantum mechanics. This other half is what people often refer to as quantum weirdness.
What people often refer to as quantum weirdness is the wave function being transformed by its mere observation. We say that the wave function collapses. This collapse is a probabilistic dynamics of the wave function. Now, even though the result of the collapse is not determined deterministically, it follows some probabilistic distribution which is defined by what the wave function was before collapsing.
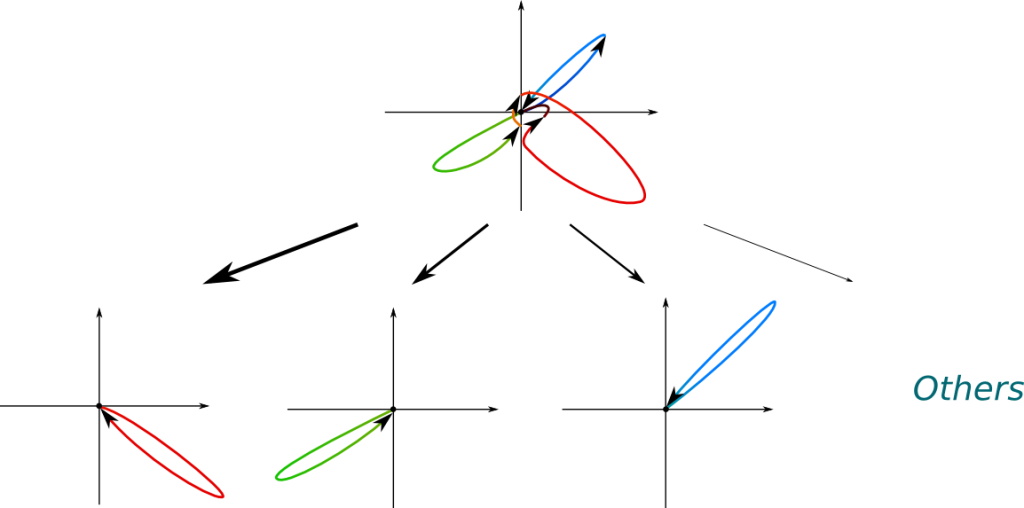
What’s extremely weird is that this probabilistic distribution depends on what’s being measured. Assume the position is measured. Then, the wave function will collapse into a localized wave function. The position of this localized wave function follows a probabilistic distribution whose density is the square of the norm of the wave function before it collapses. The following figure displays the possible collapses of a wave function, where bolder arrows correspond to more likely collapses.
In the figure above, the most likely collapses correspond to positions blue, green and red, because the distances from the origin to the value of the wave function at these points are greater. The most likely collapse is the red one.
Yes! If we remeasure the position after a wave has collapsed, then, just like the wave function, the probabilistic density function is localized at the position where the wave function first collapsed. Thus, almost surely, a second measurement will provide the same wave function, and hence the same results.
The measurement of momentum occurs very similarly to the measurement of position, but with regards to the momentum space wave function instead of the wave function. There are also several physical measures which are combinations of momenta and positions, like angular momenta. These physical measures are associated to abstract mathematical objects called operators. For instance, the Hamiltonian is the operator associated to energy. Similarly to energy, the possible values of the physical measures correspond to the eigenvalues of the operators. In many cases, these values are discrete. Any stationary wave function is then a superposition of the wave functions which correspond to these values. A measurement then collapses the wave into the wave function corresponding to the measured value.
Great question! The spin is what’s missing to describe quantum states. Now, the spin is more abstract to deal with, but it’s also much easier to manage mathematically. Indeed, while wave functions evolve in the infinite Hilbert space, spins are superpositions of 2 values: up and down. The superpositions and collapses of spins can thus be described by simple vectors and matrices. If you want to have an idea of how collapses occur mathematically without facing the complexity of Hilbert space, spins are what you should check out.
Let’s Conclude
To conclude, let me recall the two major dynamics of wave functions. On one hand, there is the deterministic revertible Schrödinger equation. Although difficult to solve, this equation can be considered as a classical one. On the other hand, there is the probabilistic collapse. This corresponds to a Markov dynamics, where the probabilities of transitions towards other quantum states are defined by the current state. As discussed in my article introducing quantum mechanics, what’s particularly weird with this latter dynamics is its non-local properties in both space and time. This boils down to the question of what a measurement does. But that’s not the weirdest thing about this other dynamics.
The way the quantum state collapses depends on what’s measured. Even worse, there is no mathematical basis to say what it means for something to be measured. In other words, what triggers the collapse? This is the core of the measurement problem.
As far as I understand, these interpretations provide explanations of why probability is involved. But I don’t see how they account for the measurement problem. Approaches which seem more promising to me on a mathematical viewpoint involve quantum information theory or particles going back in time. But, overall, I really don’t understand the measurement problem. This is where a quote Richard Feynman becomes reassuring: I think I can safely say that nobody understands quantum mechanics.



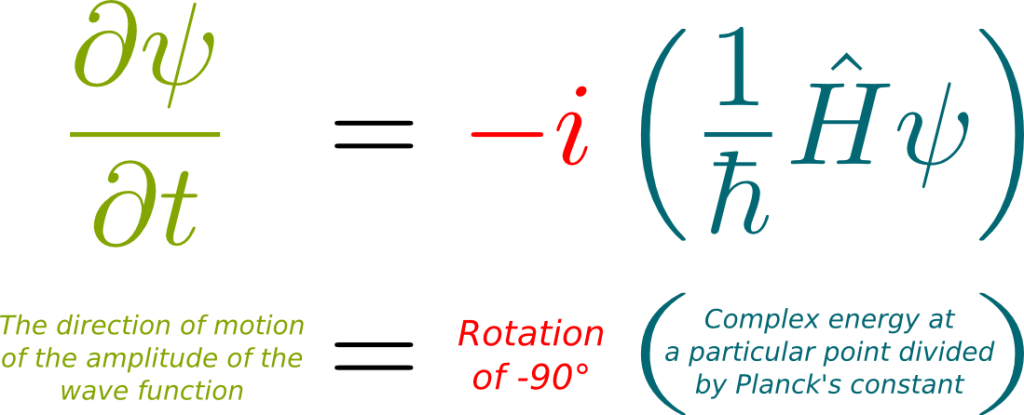

Leave a Reply