Addition is the simplest thing in mathematics, right? Wrong! On Minute Physics, Henry Reich unveils some of the most weirdest aspects of addition:
After a few basic operations, Henry ends up proving $1+2+4$+$8+16$+$…=-1$!

Hehe… It’s a bit like eating the Japanese poisonous fugu fish: If it’s done by a qualified cook, then it’s good. Otherwise, don’t put it in your mouth!
Hummm… He’s a physicist, isn’t he? More seriously though, these manipulations are extremely hard to justify, even though they do unveil something fundamental. Anyways, his not-even-one-minute crash course is definitely not enough for you to start your own fugu restaurant! Let’s see what I mean in more details…
Positive Convergent Series
Obviously, additions aren’t that complicated when they involve a finite number of terms. These are not what’s of interest for us in this article. Rather, let’s have fun with the cool infinite sums, also known as series. Now, some series aren’t as tricky as Henry’s. The simplest kinds of series are the positive convergent series.
They are sort of the non-poisonous fishes. Unless you forget them in your stove, they’ll be edible! The harder thing though is to distinguish them from other fishes.
They are series such that terms are positive and get very quickly small. The most famous example is based on Zeno’s paradoxes. One of these paradoxes is illustrated by the following video by the Open University:
The key message of this video is that adding up an infinite number of numbers can make a lot of sense. In fact, when the terms are positive and get very quickly small, it’s a very natural thing to do.
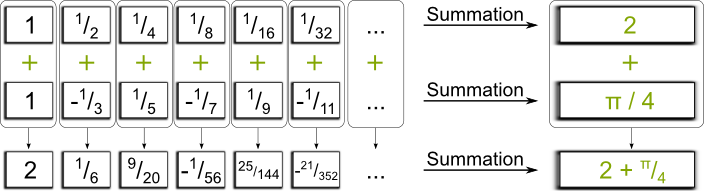
Yes! A variant of Zeno’s paradox illustrates himself walking the 2 miles to his house. He always has to walk half of the distance to the house before he gets there. So, first, he walks 1 mile. Then half a mile. Then a fourth of a mile… As you’ve guessed, each term is half of the previous one. Eventually, the total walked distance is $1+^1/_2$+$^1/_4+^1/_8$+$^1/_{16}$+$^1/_{32}+…$, which thus adds up to 2 miles he had to walk.
Yes! Here’s another illustration. Assume your restaurant (which is still not licensed to cook fugu!) is given orders of a cake. The first order is 1 cake, the second is half a cake, the third a fourth… and so on. How many cakes do you have to make? The answer is 2, as we’ve discussed and it’s illustrated by the following figure:
Positive Divergent Series
NO!!! No. No, no, no, no… No! NO. No.
I’m sorry for being so emotional here. But it’s the source of sooo many mistakes! And mistakes like that can have you cooking poisonous fishes! So let me phrase it clearly. Not all series with terms getting to zero converge.
In fact, I want you to promise me! Promise me you’ll never assert that series whose terms go to zero converge. Promise me!
Good. Let me show why such a thing is false. Consider the series $1+^1/_2$+$^1/_3+^1/_4$+$^1/_5+^1/_6…$. This series is called the harmonic series, and has played a key role in the understanding of infinity.
Yes. Let me prove it! Suppose the orders of cakes are those of the harmonic series. Let’s bake pieces accordingly. Now, if we are shrewd about the way we arrange these pieces, we can make an interesting pattern emerge! Here’s how I’ve done it:
So what I’ve done here is put the 1 aside. Then, I made a cluster of pieces containing the next piece of cake. Then a cluster with the 2 following pieces. Then with the 4 next ones. Then with the 8 next ones… And so on. Do you see the pattern I’m trying to highlight here?
Keep in mind that I’m trying to show you why the harmonic series isn’t a nice convergent series!
Bingo! But why?
Take your time to find it out by yourself!
Sure. Look at the cluster of 8 pieces. Why do the pieces add up to more than half of the cake?
There you go! In fact, that’s why I arranged the pieces like that! As you can imagine, the next cluster will have 16 pieces, all of which are of greater size than 1/32. And so on! This gives us an infinite number of clusters of pieces, all of which are at least half a cake. Thus…
Isn’t it? Mathematically, we say that the harmonic series diverges. That’s because its terms don’t get small quickly enough. I hope you’ll keep that in mind for the rest of your life!
There’s no general result for such a thing. In other words, you can always find a fish in the see which will not have been classified as safe to cook or poisonous yet. But there are several tests you can make, which would work for most of the series you’ll meet in the classrooms. I’m not going to explain these tests here, but if you can, you should write an article to explain them!
Convergent Series
So far, we’ve only discussed series with positive numbers. But additions of a finite number of terms are actually defined for many more mathematical objects. Obviously, there are also the negative numbers, but we can also add complex numbers, or even vectors! But as we try to extend the concept of infinite series for these objects, things get tricky…
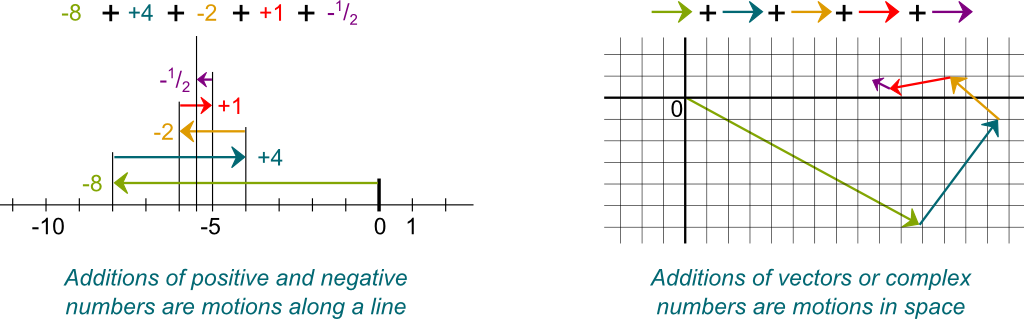
You’re reminding me that no Science4All article has been written yet on these major mathematical objects… I’ll try to fix that some day (you can fix it too, by writing your own article)! For our purpose here, we need to consider these objects (positive and negative numbers, complex numbers and vectors) as motions.
Imagine yourself in an elevator. Each number can be associated with a motion. $+2$ corresponds to a motion of 2 floors up. $-5$ is a motion of 5 floors down. Similarly, complex numbers and vectors are motions in higher dimension spaces. And, as we add up vectors, we add up the motions. In the figure below, on the left, the motion given by positive and negative numbers is a left-right motion. On the right is a motion in the plane, as expressed by complex numbers or, equivalently, 2-dimensional vectors.
Now, the figure only displays sums of a finite number of motions. But, just as we did it for positive numbers, it’s often useful to consider a sum of an infinite number of motions. In other words, let’s try to define series of motions!
Now, for the series of motions to have a value, the sum must take us towards one precise location. If a series of motions does take us to one precise location, then we say that it converges.
Absolutely Convergent Series
Hum… It’s usually hard to know! One thing that’s relevant is to look at the successive lengths of the motions.
You’re totally right! In particular, the series $1-1$+$1-1$+$1-1+…$ doesn’t converge because the sum of motions never takes us anywhere precisely! It always makes us zigzag between values 1 and 0. But it never gets to a precise location. And that’s because the lengths of the motions don’t get to 0. Therefore, as you said, for a series to converge, the lengths of motions must get to 0. But that’s not enough!
Hehe… You’re getting close to something fundamental! Lengths are positive numbers. How could you say that these positive numbers get very quickly small?
Come on! You’re so close! Look at what we’ve talked about so far!
Bingo! The series of the lengths is a positive series. And if it converges, then the series of motions can’t be moving too far away. Eventually, the motions will slow down so much that the sum of motions will be hardly moving. It will get stuck somewhere. And the series of motions will thus converge!
Sure! What about the series of positive and negative numbers of the figure above? This series is $8-4$+$2-1$+$^1/_2-^1/_4+…$. The lengths of the motions are 8, 4, 2, 1… thus, the series of lengths is $8+4$+$2+1$+$^1/_2$+$^1/_4+…$. If we get rid of the 3 first terms, then we obtain the geometric series we discussed at the beginning of this article! This series converges, thus, so does the series $8-4$+$2-1$+$^1/_2-^1/_4+…$.
No! The two conditions are not equivalent! The convergence of the series of lengths is a sufficient condition for the series of motions to converge, but it’s not necessary. In other words, if the series of lengths converges, then so does the series of motions. But the series of lengths doesn’t need to converge for the series of motions to converge.
Great! Now, the case where the series of lengths do converge too is so interesting that mathematicians have named it. Series whose series of lengths converge are called absolutely convergent series.
In the fish kingdom, these absolutely convergent series are like sweet harmless tuna: They are easy to cook and relatively easy to recognize. But they are plenty of other edible non-poisonous fishes in the see! And some are delicious!
Conditionally Convergent Series
As I said, not all convergent series are absolutely convergent. These convergent-but-not-absolutely series are more simply called conditionally convergent series. These aren’t as dangerous as the fugu fish, but they are already quite tricky to cook.
For a start, they may be harder to identify in general. There is the special case of alternating series which is easy to recognize, as well as a few other particular cases. But, apart from that, proving that a series is conditionally convergent is often quite difficult. But that’s not why conditionally convergent series are very tricky.
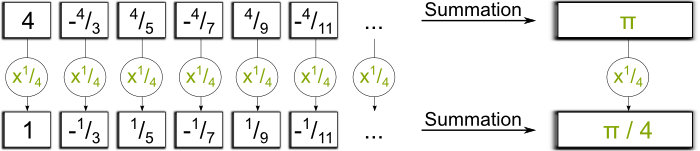
Let’s take an example. And I can’t resist to involving one particular famous conditionally convergent series… This famous series is $4-^4/_3$+$^4/_5-^4/_7$+$^4/_9-^4/_{11}+…$. This series is known as Leibniz series, and it first was studied by Madhava in India. Surprisingly, it equals $\pi$!
Hummm… It’d be a bit long to explain it. It has to do with the Taylor series of the function $arctan$. But that’s not what I want to talk about.
Yes. What’s extremely weird with conditionally convergent series is that the order in which the addition is made strongly matters!
It is weird! But it’s quite understandable when you think about it! Leibniz series has an infinite number of positive terms, as well as an infinite number of negative terms. And since it is not absolutely convergent, the series of positive terms must diverge.
If the series of positive terms converged, then, for Leibniz series to converge, the series of the negative terms should converge too. But the series of lengths is the sum of the series of positive terms and the series of the absolute values of the negative terms, and would thus be finite. That’s in contradiction with the conditional convergence!
Yes! And so does the series of negative terms. This had a dramatic consequence: By reordering the terms of the series, we can make the series equal anything we want! This is known as the Riemann series theorem.
Easy! Depending on whether the current position is below or above 1 billion, we add a positive or a negative motion to get it close to 1 billion. It’s as simple as that, and is done in the figure below:
Eventually, we’ll be zigzagging around 1 billion. But, because the initial series of motions is convergent, the lengths of motions eventually go to 0. Since we cannot exceed 1 billion by more than the lengths of the motions, we won’t be exceeding it by much eventually. Likewise, we’ll eventually never be much below. This argument indicates that the series equals 1 billion.
I know! That’s why you must be cautious with infinite series, or you’ll end up proving $\pi=4-^4/_3$+$^4/_5-^4/_7$+$^4/_9-^4/_{11}+…$=$1,000,000,000$.
They are! Not only can you not rearrange the terms, you can’t combine them to simplify the sum either! Otherwise, you could even prove $1=0$, as James Grime does it on Numberphile:
Be careful with what you do with series, and think twice before buying a result, especially if its yours. Just like you should think twice before putting fugu in your mouth!
We’re getting there…
Super-Summation
The trick is to consider the summation of a series as an operator which transforms a sequence of motions into an overall motion… when it’s possible. Below are some of the mappings made by this operator we have discussed so far.
I have. This last one can be shown to be conditionally convergent. It thus has a value, but I don’t know it. Still, it’s important to note that it has some value. On the contrary, the first, third and fourth series have no value, because they are divergent.
We could. But this would conceal something amazing about infinite series! That’s why it’s better to give them no value… so far.
Hehe… You see right through me! And the key idea is to define a better concept of summation. Let’s call it a super-summation. This terminology is absolutely not conventional, but I find it very appropriate.
Let’s rather focus on what our super-summation needs to be capable of. First, just like Clark Kent, the super-summation must be able to pass exactly for a classical summation for the classical situations the classical summation can handle. This means that the super-summation must operate identically to the classical summation on convergent series. This condition is known as regularity.
You’re totally right! There are in fact plenty of super-summations which satisfy the condition I’ve given so far. And they sometimes give different values to a same series!
Some super-summations are more natural than others though, and they have applications to physics! Some of them are obtained by averaging the successive overall motions. James Grime explains such a super-summation, known as the Cesaro summation in the sequel of the Numberphile video. And there are more powerful such averaging super-summations, like the Abel summation or the Borel summation. However, these technics can’t sum Henry’s series…
Henry mentions it briefly and indirectly… But it’s impossible for you to guess if you’ve never heard of it! The more powerful super-summation Henry hints at is based on analytic continuation. Analytic continuation is a very useful technic in mathematics. For instance, it’s the core idea of the construction of the famous Riemann zeta function. But it’s also a bit long to explain, and I won’t do it here.
Yes! And after a few pages of rigorous proof, we can prove that indeed, it’s natural to assume $1+2+4$+$8+16$+$…=-1$!
Linearity and Stability
No, indeed. To better understand what he did, we need to introduce each rule of manipulations he used.
There are three of them, and it’s natural to extend them, as they already work on convergent series. First, if we multiply all the terms of a convergent series by a constant number, then the sum must be multiplied by this constant number. As done below:
Second, if we take two convergent series and we add their terms one by one, the series we obtain must have a sum which is the sum of the two initial convergent series.
The two manipulations here are known as linearity. In other words, the summation is linear. Because of that, we want the super-summation to be linear too.
The third and last manipulation is stability. It’s the most natural one. It says that if we insert a 0 in front of a series, then the summation must keep the same value.
The manipulations enable us to obtain an equation which Henry’s series must satisfy. Come on! Give it a try!
OK, I’ll do it. But that’s only because we’re getting to the end of this article! Insert a zero before Henry’s series. You obtain $0+1+2+4$+$8+16+…$. Multiply that by 2. You obtain the series $0+2+4+8$+$16+32+…$. Now, subtract Henry’s series term by term, and you end up with $(-1)+0+0$+$0+0+…$, which is a convergent series adding up to -1. Thus, twice Henry’s series minus itself equals -1. This indicates that Henry’s series equals -1. Sweet, isn’t it?
Hummm… It took me a while to be sure of it, but the answer is yes, because there exists a unique natural regular linear stable super-summation extended to all divergent geometric series but $1+1+1$+$1+…$. And the justification is very tricky. You’d better be a damn’ good cook before you try such manipulations! Indeed, you can’t do these manipulations on just any divergent series!
Take the series $1+1+1$+$1+1+…$. Add a zero and subtract itself. You obtain $(0+1+1+1+1+…)$-$(1+1+1+1+1+…)$=$(-1)+0+0$+$0+0+…$, which is a convergent series which equals -1. But we’ve subtracted the series to itself, and we should have therefore obtained 0. That’s contradictory and shows that the series $1+1$+$1+1+1+…$ is not summable by any regular linear stable super-summation, even though it can be reduced to a convergent series using our manipulations. That’s how tricky divergent series are! Also, beware that you can’t add an infinite number of 0s without affecting the sum. Indeed, using Cesaro’s super-summation, you can prove that $1+0-1$+$1+0-1$+$1+0-1+…$=$2/3$! Thus, $1+0-1$+$1+0-1$+$…\neq 1$-$1+1-1$+$1-1+…$. Disturbing, right? The key is to understand the signs $+$ no longer stand for the addition we are familiar with!
An easy answer is to tell you to apply proven theorems only! If you can’t manage them, don’t cook divergent series! However, as long as you don’t eat them, you can always play with them (even though that goes against my mom saying I should never play with food!). This is what the greatest mathematicians like Euler have been doing for years, even though they had no justifications for that. This led him to amazing results, such as $1+^1/_4+^1/_9$+$^1/_{16}+^1/_{25}$+$…$=$\pi^2/6$. And, hopefully, after some playtime, you’ll end up with something fundamental… The more modern mathematician method though would be to define a super-summation as a mapping of sequences with a number, and to prove some convincing properties of this super-summation, as done by Hardy and Ramanujan.
Let’s Conclude
I bet you didn’t expect addition to be that complicated! I know I didn’t… To sum up, know that if a series is not absolutely convergent, then it’s a tricky series. This is even more true if it’s not convergent at all! In this case, be careful with what you can and what you can’t do! More often than not, the manipulations you undertake may lead you to some contradictory $1=0$… That’s why, at school, you won’t be dealing with divergent series, even though they are so cool!
You’ve got to admit that it’s amusing that simple manipulations like Henry’s retrieve a value for divergent series! But that’s not all! Surprisingly, these super-summations also have incredible applications in physics, and quantum field theory in particular, with astonishingly accurate predictions! There’s this great article by Christiane Rousseau also on using divergent series to solve and understand differential equation. Unfortunately, my knowledge is more than limited in this area… at least so far.
For Math Guys…
In the general case, manipulations like Henry’s can’t be allowed. They may lead to paradoxical conclusions such as $1=0$, like when we’re applying them to series like $1+1+1$+$1+…$.
OK. I’ll have to be technical here… Let $\mathbb R^{\mathbb N}$ the set of infinite real sequences. It’s a vector space. The set $C$ of sequences whose series converge forms a vector subspace, on which the classical definition $S$ is well-defined and is a linear form. Plus, let $e$ be the insertion of a zero ahead of a sequence. It’s a linear mapping for which $C$ stable. Now, what’s important to note is that the vector space spanned by the sequence $u=(1,2$,$4,8,16,…)$ is in direct sum with $C$. Thus, any vector of $v \in C\oplus u\mathbb R$ is uniquely decomposable into $v=c$+$\alpha u$, where $c \in C$ and $\alpha \in \mathbb R$. We can thus define the super-summation on $T$ on $C\oplus u\mathbb R$ by $T(v)$=$S(c)-\alpha$. This super-summation is linear by construction.
Exactly! Now, note that $T(e(v)) $=$ T(e(c)+\alpha e(u)) $=$ T(e(c)) $+$ \alpha T(e(u))$. Now, since $c \in C$ and $C$ is stable by $e$, we have $e(c) \in C$, thus $T(e(c)) $=$ S(e(c)) $=$ S(c) $=$ T(c)$. What’s more, note that $e(u) $=$ u/2-{\bf 1}/2$, where ${\bf 1} $=$ (1,0,0$,$0,0,…)$. Thus, by linearity, $T(e(u)) $=$ T(u)/2 $-$ T({\bf 1})/2$. But ${\bf 1}$ is convergent, thus $T({\bf 1}) $=$ S({\bf 1})=1$. Therefore, using $T(u)=-1$, we have $T(e(u)) $=$ T(u)/2 $-$ T({\bf 1})/2 $=$ -^1/_2 – ^1/_2 $=$ -1$… which is $T(u)$! Phew… It works! We have $T(e(v))=T(v)$ for all $v \in C\oplus u\mathbb R$.
All but $1+1+1$+$1+…$! This is because the set of divergent geometric series $u_x$=$(1,x,x^2$,$x^3,x^4,…)$ with $x \leq -1$ or $x > 1$ forms a free family (hence enabling a well-defined super-summation), and that they are related to convergent series by $e$ with $e(u_x) $=$ u_x/x$-${\bf 1}/x$ (hence guaranteeing $T(e(u_x)) $=$ T(u_x)$, provided that $T(u_x) $=$ 1/(1-x)$). Hence, a unique natural linear regular stable super-summation exists for $C \oplus (\oplus_{x \notin ]-1,1]} u_x\mathbb R$).
Hehe… For one thing, we can include bounded series which can be summed using Cesaro or other regular linear stable super-summation, as the terms of these series are in direct sum with divergent geometric series. We can do even better! In fact, it seems that all sequences $u$ for which the next element $u_{n+1}$ is obtained by a linear combination of a finite number of the previous ones (for $n$ high enough) can be added, if the sum of the coefficients of the linear combination isn’t 1. In other words, if $u_{n+1} $=$ \sum_{0\leq j \leq k} a_j u_{n-j}$ with $\sum a_j \neq 1$, then I think $u$ can be added (but I’m not sure as I haven’t tried to prove that!).
Apart from that, I have no idea! What I do know is that there is no linear regular stable super-summation defined on a space that would contain series like $1+1+1+1+…$ or $1+2+3+4+5+…$. Surely, enough, you can follow the manipulations explained by Tony Padilla on Numberphile.
Still, this calculation is fundamentally wrong (as well as the other first proof by Ep Copeland). As Rémi Peyre commented it on ScienceÉtonnante, $S(1,2,3,4,…) $-$ 2S(e(1,2,3,4,…)) $+$ S(e^2(1,2,3,4,…)) $=$ S(1,2,3,4,…) $-$ 2S(0,1,2,3,4,…) $+$ S(0,0,1,2,3,4,…) $=$ S(1,0,0,0,…) $=$1$ using linearity, but also equals $S(1,2,3,4,…)$-$2S(1,2,3,4,…)$+$S(1,2,3,4,…) = 0$ using stability, hence proving $1=0$. Thus, once again, there is no linear regular stable super-summation defined on a space that would contain series like $1+1+1+1+…$ or $1+2+3+4+5+…$.
Yet, what’s particularly troubling is that several methods lead to the result $1+2+3+4$+$5+…$=$-^1/_{12}$. Worse, this very formula finds applications in string theory and in computing the Casimir force in theoretical physics! In other words, it really seems true… But I don’t know why!
Analytic continuation applied to the Riemann zeta function does sort of indicate this result. However, I don’t know if there doesn’t exist any other analytic continuation which would produce another result for the series $1+2+3+4$+$5+…$. I have no idea! As a mathematician, what I do claim is that I haven’t been convinced so far mathematically by the relevancy of defining $1+2+3+4$+$5+… = -1/12$. Rather, and that’s strongly based on my ignorance of the topic, I’d say that there is an underlying algebra we haven’t uncovered yet… But this is the voice of my young audacious naive arrogant mind speaking!
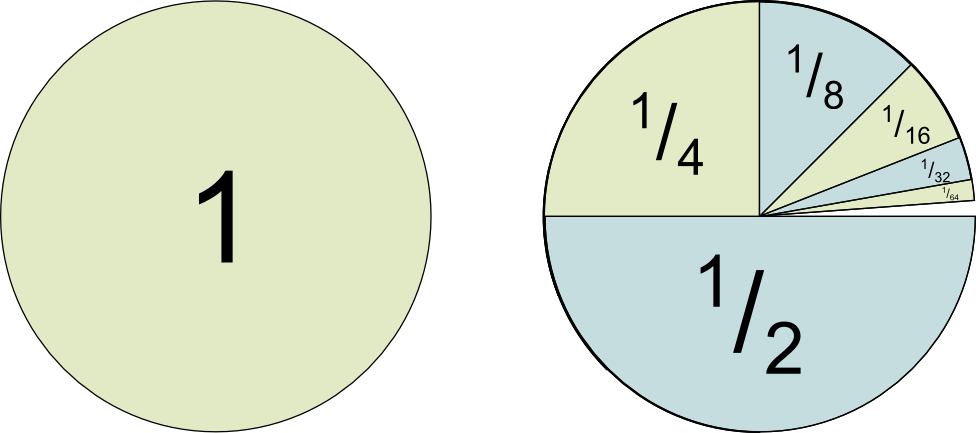


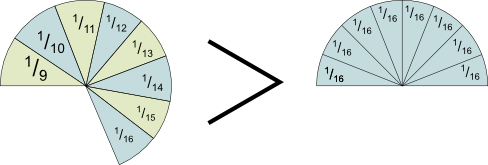

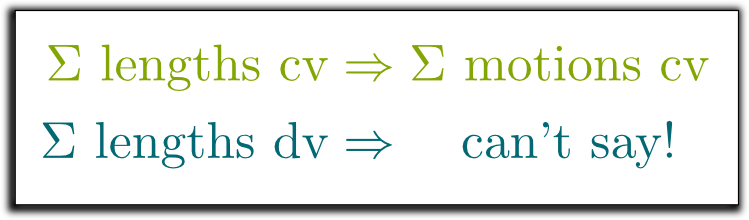



Leave a Reply