To introduce this article, I’ve searched for cool Youtube videos. But instead, I found many terribly wrong explanations. Here’s the worst I found.
Oh my god! So many things are wrong!
Like the absence of gravity on the Moon (how did we even land and walk there then?), the idea that because an apple can’t fall up to the sky, it has to fall down (what about satellites?) or the explanation that the Moon doesn’t fall on the ground because Earth is bigger (what? Just… what?). But what’s even worse to me is the huge lack of critical thinking. Whether kids are naturally curious or not, their curiosity is shattered by such poor explanations, because such explanations have them thinking that vague, imprecise and fuzzy arguments suffice to make a point! This is typically the wrong way of teaching science (or anything else for that matter)! It is so wrong! So, so wrong!
Sorry I lost my temper… Back to gravity. As you’ve guessed, gravity is very badly presented in this video. Gravity is not some force big objects exert on smaller ones!
It would take several of mankind’s greatest minds to provide answers to this question. And even they often got it wrong. In fact, today’s greatest scientists are still deeply puzzled by gravity. To give an idea, some serious string theorists now claim that most of the gravity of our universe might be caused by some parallel universe!
Yes, you read that right. But don’t worry, in this article, I won’t get there (mainly because I don’t understand much of string theory…). I’ll only talk about well-established relevant theories of gravity and where they got things wrong. As you’ll see, that’s already mind-blowing!
Galileo’s Gravity
The first mind-blowing thing about gravity is unveiled by the following awesome video by Derek Müller on Veritasium.
Actually, Derek’s explanation is wrong (but his video is nevertheless the right way of teaching science, as it is based on inquiry, critical thinking and experiment!). Einstein would prove it wrong. But we’ll get to that. For now, let’s ponder the already surprising results of the experiments he asked people to do.
Derek’s experiment is a replica of one of the most important experiment in the History of science. Ancient Greek philosophers had long ago debated the matter of falling objects, and Aristotle had concluded that heavier objects must fall faster than lighter ones. Yet, somehow, no one ever thought of putting this claim to the test. It is quite surprising that it was only in 1589 that someone dared to question Aristotle. This someone was not just anyone…
It was Galileo Galilei, the father of science. As the story goes, Galileo threw two balls of very different weights from the top of the Pisa tower. The heavy one arrived only shortly before, but Galileo explained this short delay by a difference of air resistance. If it weren’t for air, all objects would fall equally fast.
I agree. In fact, it seems that Galileo’s conclusion had nothing to do with this experiment (which apparently wasn’t even done!). After all, the results of this experiment is perfectly in accordance with Aristotle’s ideas. Instead, Galileo derived his conclusion from a brilliant thought experiment. This thought experiment would prove that Aristotle’s theory of gravity was self-contradictory.
Consider a heavy bowling ball and a lighter basketball connected by a string. Would this fall faster than the bowling ball alone?
On one hand, according to Aristotle’s theory, the basketball will fall slower, and will thus slow down the bowling ball it is attached to. Thus, together, the bowling ball and the basketballs should be slower than the bowling ball alone.
However, on the other hand, the bowling ball and the basketball as a whole are heavier than the bowling ball alone. Thus, still according to Aristotle’s theory, as a whole, the bowling ball and the basketball should fall faster than the bowling ball alone. Therefore, Aristotle’s theory predicts both one thing and its opposite. The theory is self-contradictory!
I know! I can’t believe it isn’t taught at school, as it is a wonderful example of rigorous, clever and History-changing reasoning! So good, that I had to make a video out of it, on the Science4All Youtube channel:
And there’s more… Aristotle thought that objects were falling at different speeds according to their weights. But, cleverly, Galileo noticed that gravity didn’t determine the speed of falling objects. Instead, it determined their accelerations.
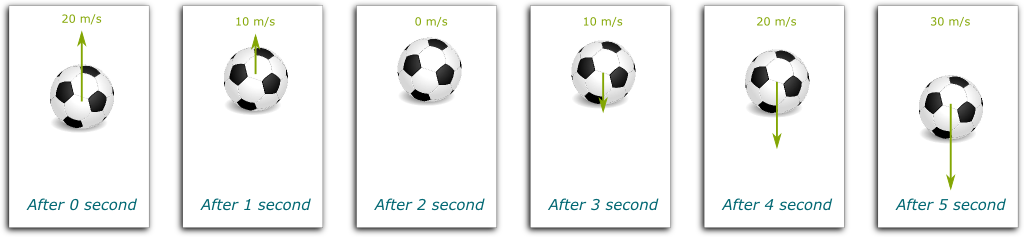
Throw a ball upwards. It is evidently not falling down at a constant speed, since it is not even falling down. Yet, for Galileo, it was already in free fall, and there weren’t much fundamental difference between a ball going upwards and a ball going downwards. In fact, imagine that you threw the object upwards at a speed of 20 meters per second. Then, Galileo noticed that, the next second, it would slow down its upwards motion, and be going upwards at 10 meters per second. After two seconds it would no longer be going upwards. After three seconds, it would start falling down at 10 meters per second.
Exactly! Galileo noticed that the downwards speed would increase by 10 meters per second every second. In more rigorous terms, Galileo figured out that gravity caused a downwards acceleration of 10 meters per second square. Somehow, this brilliant insight was deeper than Newton’s laws of motions, but it would take Einstein’s great mind to understand this. We’ll get there. For now, let’s talk about Newton’s gravity.
Newton’s Gravity
Newton’s gravity is the most useful theory of gravity we have today. When we launch rockets, all computations are based on Newton’s laws. This is how reliable they are! And that’s why we learn Newton’s gravity at school. But, evidently, as Derek showed it in the next Veritasium video, this doesn’t mean that it is well understood by most people — probably because of awful misleading popular accounts of gravity like the dreadful cartoon video that introduced this article…
For Newton, gravity is some underlying force that pulls any two objects with mass together. As Derek hinted at it, this means that, weirdly enough, your body pulls gravitationally every object of the Universe with mass, including the Andromeda galaxy!
You’re right. In fact, Newton figured out exactly the rate at which gravity decreases with distance: Accordingly to the inverse square law. This means that if you travel 2 times further away from a star, then the gravitational pull you exerts on the star will be decreased by a factor 4. And if you’re 3 times further, it will be divided by 9.
One lousy explanation may come from how diffused gravitational pulls become. After all, the intensity of light follows this inverse square law too! Well, sort of… as explained by Derek:
So I guess, following this analogy, that we may say that you are pulling everything around you at all times, but that this pull gets smeared out as you are reaching further and further. And that’s because the area of the sphere corresponding to a distance increases as the square of the distance.
This wouldn’t convince me, and I don’t think it would convince Newton’s colleagues.
As the story goes, Edmond Halley once asked Newton how an inverse square law of gravity would affect planetary motion. Newton merely answered: “An ellipse”. At that point, Newton probably realized the importance of publicizing the discoveries he had made decades earlier. He sat down for a year and a half, and wrote the Principia Mathematica. In this masterpiece, Newton defined his laws of mechanics and gravity. I also told the story of this amazing achievement on the Science4All Youtube channel:
He also provided the wonderfully illustrative cannonball thought experiment. This was the conclusive argument that put Newton’s theories on a pedestal, as explained in this beautiful extract from a NOVA documentary:
It’s a powerful way to bridge Galileo’s description of falling object and Kepler’s law of planetary motion, by showing a continuum between these two. Consider a cannonball shot from the top of a mountain and the speed it is shot at. For small speeds, the cannonball will fall accordingly to Galileo’s parabola. But when the speed is suddenly large enough for the cannonball to go around the earth, its trajectory becomes Kepler’s ellipsis. And, amazingly, Newton formally derived this great unification from his laws of motion and gravity. Hats off Isaac!
This merging of the Earth and the Cosmos also has a surprising implication, which will be key to Einstein’s insight. Intuitively, bigger objects have stronger gravitational pulls. This suggests that the gravitational pull of an object A on an object B is proportional to some measure of the “size of A”. Since this quantity is related to gravity, let’s call it the gravitational mass.
In Newton’s framework to understand the universe, yes. Namely, objects have a tendency to maintain their states of motions. And the bigger the object, the harder it is to affect its motion. Have you ever tried to push a plane?
Well, me neither. But I’m told that, even if the plane is on wheels, it’s impossible. And that’s because the plane is huge, and thus wants to maintain its state of motion. This property is called inertia, and the extent to which an object will maintain its motion is called the inertial mass. Once again, inertial mass is a measure of the sizes of stuffs.
This is what Derek explains in the following brilliant video:
You’re right. A priori, these are different. But here’s the tricky part. By merging the Earth and the heavens, Newton’s laws of mechanics and gravity must in particular coincide with Galileo’s law of falling objects. Yet, Galileo said that all falling objects undergo the same acceleration. Therefore, it must be that, for any object, the weight that pulls it down and the inertia that prevents it from being pulled down must somehow cancel. A short computation then tells you that the gravitational mass and the inertial mass must coincide. What a puzzling coincidence!
Einstein’s Gravity
It’s hard to stress how indisputable Newton’s brilliant laws of mechanics became. Their elegance, accuracy and usefulness raised Newton to the status of God of the human intellect. It seemed that he had figured it all out, and that his words were definite truth. Well, they weren’t. In fact, his ideas were fundamentally wrong.
Yes! The hints that led Einstein to overthrow Newton were numerous. First, there were both theoretical and experimental evidence that the speed of light was the same for all observers. In 1905, this led Einstein to model spacetime as a single intertwined entity in which, among other weird things, speed slowed the passage of time. Einstein’s model is now called special relativity. I explained its core principles in the following video:
Second, Newton himself confessed that he had no explanation for the instantaneous force at a distance he had called gravity. He wrote: “Gravity must be caused by an agent, acting constantly according to certain laws; but whether this agent be material or immaterial, I have left to the consideration of my readers.” This acknowledgement of weakness must have deeply resonated in Einstein’s mind, as his special relativity implied that nothing in the universe could be instantaneous — thus gravity cannot travel than light. And perhaps that, armed with his newfound theory of special relativity that bent his image of spacetime, he figured out that spacetime could be that agent that Newton was referring to.
Clearly! But there’s more. Einstein didn’t like that Newton’s theory required the equality of gravitational and inertial masses to match observation. He famously asked: “Did God have a choice in creating the universe?” What he meant by that is that a theory of physics would be more satisfying if it did not require apparently arbitrary ad hoc choices — like assuming that the gravitational and inertial masses were equal. In 1907, Einstein realized that the puzzle of masses was a hint of a more fundamental principle, which he called equivalence principle. This equivalence principle asserts that gravitation is not a force; it is acceleration.
The equivalence principle is a pretty tricky but absolutely brilliant idea. In fact, Einstein would later call it the happiest thought of his life! But I’ll get back to this. Importantly, the equivalence principle fundamentally Einstein’s approach to physics.
Einstein was so seduced by the equivalence principle that he didn’t hesitate to embark on an 8-year epic and anxious quest for a consistent theory of gravity. Here’s what he later said about this period of his life: “The years of searching in the dark for a truth that one feels but cannot express, the intense desire and the alternations of confidence and misgiving until one breaks through to clarity and understanding, are known only to those who have themselves experienced them”. This is my favourite testimony of what it means to do research.
A major piece of the puzzle then came from a fourth weakness in Newton’s theory. Namely, Einstein saw a major flaw in Newton’s first law.
It’s the most obvious one, and is often called the law of inertia: “Objects tend to maintain their states of motions”. What’s often forgotten is that it only holds in so-called inertial frames of reference.
Exactly! What is that? While Galileo and Newton would claim that most frames of reference are more or less inertial, neither they nor other scientists gave a consistent definition of inertial frames of references. If you don’t believe me, just check wikipedia’s definition, and you’ll see that it is essentially a circular definition. Physicists around Einstein’s time ended up assuming that there was such a thing as a universal static aether, but it seemed to create many more problems than it solved. Einstein’s big idea was to realize that this was a hint that there was no such thing as an inertial frame of reference! What a breakthrough!
As the (definitely false) story goes, Einstein once saw a man falling from a roof. He rushed to the man and asked him: “Did you feel gravity when you were falling?” The man supposedly said no. The next day, Einstein wrote: “The gravitational field has only a relative existence… Because for an observer freely falling from the roof of a house – at least in his immediate surroundings – there exists no gravitational field.” Einstein would later call this “the happiest thought of my life”.
What Einstein realized is that free fall is the natural frame of reference of the universe, because it is the frame of reference in which observers do not feel gravity. This should shed even more light on Derek’s next awesome video on weightlessness:
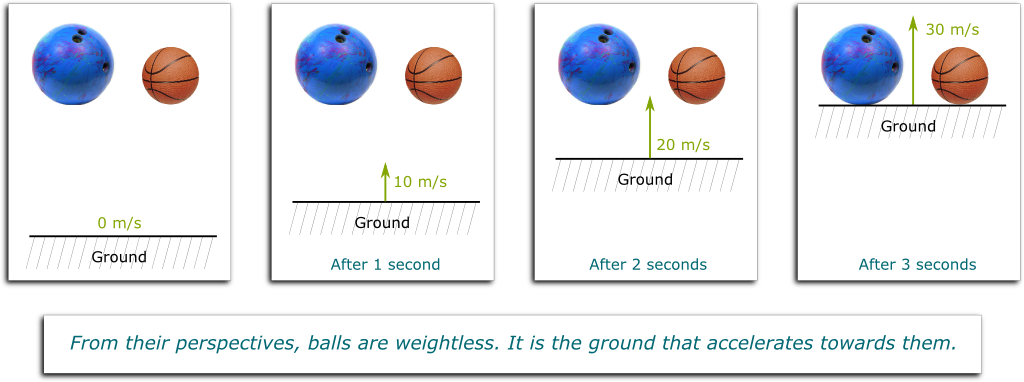
Derek explained that astronauts in space stations feel weightless because both are accelerating at the same rate. This is the Newtonian picture of the world. In this picture, astronauts’ weightlessness is a mere illusion. Not in Einstein’s view of the world. For Einstein, they are weightless because they are in a natural frame of reference — that is, one where observers do not feel gravity. This brilliant insight is the topic of what I think is my best video so far:
It really is! And the main reason why Einstein’s vision of the world is such a hard idea to grasp is that most of us have never really been in a natural frame of reference. The frame of reference of the surface of a point on the Earth, say, of Montreal, is one where we do feel gravity. This is because, according to Einstein, Montreal is accelerating. And, more or less like in Newton’s mechanics, accelerating frames of reference are not natural. They feel gravity.
No, it’s the opposite! Montreal is constantly accelerating upwards, at the well-known rate of 9.81 m/s2. That’s why two balls of different weights hit the ground at the same time: In their weightless natural frame of reference, they’re both still, and it’s the surface of the Earth that accelerate and reach them. It’s not then surprising that the ground reaches them both at the same time. Now, this really makes sense.
Let’s now have another of Einstein’s thought experiments! Picture yourself standing in an elevator accelerating upwards. You feel heavier. Einstein’s great insight was to see that this upwards acceleration of a frame of reference is indistinguishable from gravity. In effect, you might as well say that it is gravity.
Do not say that to your high school physics teacher, as in Newtonian physics, this sentence is regarded as deeply false! But, in Einstein’s general relativity, I’d say that it’s quite accurate. More precisely, elevators that accelerate upwards are frames of reference with greater gravity.
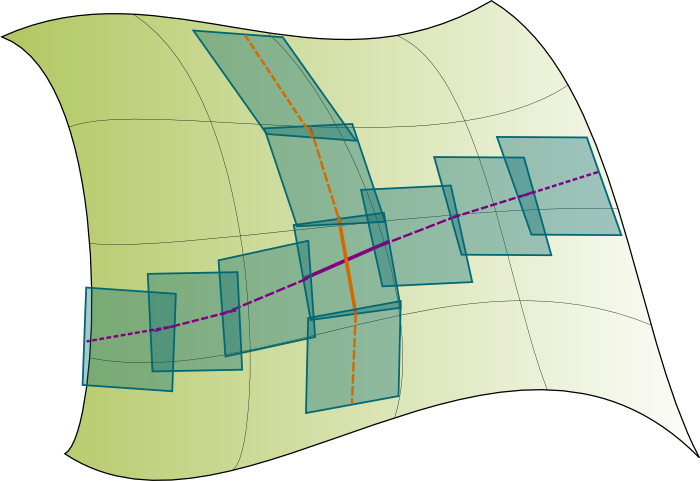
This sounds ridiculous, doesn’t it? The surface of the Earth is roughly a sphere, and, given that it accelerates outwards, you’d expect the sphere to expand. But Einstein had a brilliant explanation for why it doesn’t: Spacetime is curved, and gravity was the cause of it!
Natural frames of reference are not curved; they go “straight”. But their straightness undergoes the curvature of spacetime, which itself is due to gravity. It is because of this curvature of spacetime that the natural frames of reference look curved from one another’s perspective. For instance, for the free falling Earth, the weightless free falling balls seem to have their trajectories curve towards the Earth centre — but, once again, this is only because spacetime is curved, not because the trajectories are curved!
I’m sorry, but the curvature of spacetime is extremely hard to grasp. And you’re definitely not the only one struggling to visualize general relativity. In fact, after years of anxious search, Einstein still hadn’t figured it out. He couldn’t write down in a rigorous way the curving of spacetime by gravity. Yet, at some point, he had to give a talk about his still ongoing work. One of the greatest mathematicians of all times, David Hilbert, attended the talk. Hilbert probably got annoyed by the gaps in Einstein’s work, as he declared: “Physics is too important to be left to the physicists”. Hilbert went back to his office and raced Einstein in the formulation of general relativity. This was a huge threat to Einstein. Einstein feared he’d lose the credits for his theory. Einstein rushed back into the mathematics of Riemann’s non-Euclidean geometry. He made uncountably many attempts, but all were filled with errors. Until, suddenly… He got it! At last, he had formulated the magnificent theory of general relativity and published the beautiful fundamental equation of gravity.
To check his equation, Einstein computed the trajectory of Mercury, which was known to be inconsistent with Newton’s laws. After pages of painstaking calculations, he found a near perfect match. This got him so excited that he had heart palpitations for hours! That was it! Einstein had triumphed!
For reasons beyond me, experimental physicists weren’t convinced yet. They wanted Einstein to make a prediction that could be tested. He then proposed the famous solar eclipse experiment. This would take four years to be performed, not without thrilling ups and downs. At last, Sir Arthur Eddington got the results: Newton’s mechanics was overthrown by general relativity. This made Einstein a world-famous star overnight and the new icon of scientific genius!
When asked about would have been his reaction if Eddington had proven relativity wrong, Einstein famously made the quip: “Then I would feel sorry for the dear Lord; the theory is correct.” Frankly, I too find this theory too elegant to be wrong. It solves all the troubles of Newton’s mechanics by invoking Riemann’s surprisingly natural generalization of the narrow and egocentric Euclidean geometry and by involving crystal-clear principles! It had to be right. All I hope is that I’ve managed to convey this irrational thought.
Let’s Conclude
My irrational thought that general relativity must be right is wrong. We know it. Einstein’s theory can’t be the end of it, most importantly because it is in contradiction with the most accurate theory of physics we have ever come up with, quantum mechanics. Both theories seem so right, but both can’t be simultaneously right. Gravity is still a puzzle. In fact, it’s probably more a puzzle today than it has ever been in the past. After all, both Newton and Einstein were nearly alone in their times to question established theories of gravity. Conversely, today, many physicists are developing revolutionary models of gravity. Here’s one video about one of these models, as it discussed a 2014 discovery on quantum gravity:
Don’t ask me about gravitons and how they make balls fall though. It’s far, far beyond my understanding of gravity. At least, so far.

Leave a Reply