What a world cup! As I’m writing this article, the group phase is still not over and we have already seen a myriad of breathtaking goals and a bunch of memorable games! Also, as opposed to the 2010 world cup, the big stars have all scored or played fantastically (except Ronaldo?). Yet, none of these stars has had nearly as much TV time as the true big star of the World Cup. This big star appears in all games and gets more slow-mo replays than any one else.
I’m talking about Brazuca.
Brazuca is the official ball of the World Cup. She (he?) is the one that billions of people are following with their eyes, as they hope that she will activate the infamous goal-line technology! Sadly, this big star of the World Cup doesn’t get enough focus from the medias. And yet, there’s a lot to say about Brazuca. As I’ve just read it in this mind-blowing article in French by Étienne Ghys, Brazuca is a cube!
Hummm… Are they? Historically, balls used to be made of leather. And they were not round, mainly because sewing a perfect sphere is a very tricky thing to do. Since then, Adidas has replaced the sewing by gluing, but it kept the tradition of making balls out of flat panels, as displayed in the following video:
Before explaining why Brazuca is a cube, let’s first review the geometry of the classical football balls.
Classical Balls
Sewing a round ball is no piece of cake. What are easier is to make are polyhedra like cubes, octahedra, icosahedra….
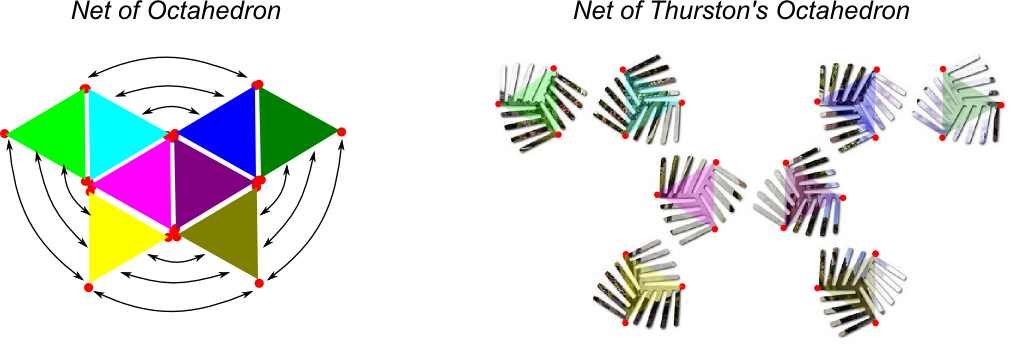
A polyhedron is a volume delimited by flat faces. Polyhedra play a central role in (linear) optimization. But in our case, what’s interesting about polyhedra is that they are relatively easy to construct from nets. Indeed, you just need to cut polygons in the form of the faces of the polyhedra, and to glue (or sew) them accordingly to a net. Here’s an example for the cube:
Now, the best polyhedron to make up a football ball should be as symmetric as possible. After all, a football player shouldn’t have to worry about which side of the polyhedron he will hit. Yet, one of the most beautiful Ancient theorem of mathematics precisely state that they aren’t that many polyhedra whose faces are all perfectly symmetric. As a matter fact, 2,000 years ago, Plato had proved that there were only 5 such polyhedra.
The proof of this surprising fact is another beautiful piece of mathematics, and is explained in this great video by Numberphile:
Now, if we restrict ourselves to perfectly symmetric polyhedra, we’ll have to choose among these 5 symmetric solids. Then, naturally, the roundest of them all will be the one with the most faces, that is, the icosahedron.
Humm… You’re right. So let’s cut the pointy corners!
By doing so, you can imagine that we’ll add three edges to every triangle (which will thus become a 6-edge hexagon). Plus, because there are 5 faces adjacent to each corner, every cut corner will produce a pentagon (5-edge polygon). Eventually, the polyhedron we’ll obtain is a so-called truncated icosahedron. Doesn’t this polyhedron remind you of something?
It is! And that’s because the truncated icosahedron is the rounding of the roundest Platonic solid!
Exactly. Faces are slightly rounded, because of the stretchability of the material. However, they are not rounded for geometrical reasons. And, from the look of it, we’ve reached some mathematical limit, unless we increase indefinitely the number of faces to the point where the ball has more sewing than faces…
Curved Nets
But designers and engineers at Adidas have more than one trick up their sleeves. And their beautiful baby, Brazuca, is a proof of that.
Curved edges! While we cannot curve flat sheets of paper (as will be discussed later), we can cut faces with curved edges, and glue (are sew) accordingly. In the case of 2 faces, a surprising theorem by Pogorelov asserts that, as long as the edges of the 2 faces are of the same lengths (and as long as some conditions about curvatures of edges hold), we will always be able to glue the two edges, hence forming the outer layer of a 3-dimensional solid. Here’s an illustration of that theorem:
Hehe… Do you know how tennis balls are made? It’s time to have a look with this video:
As it turns out, tennis balls are made by gluing together two flat sheets of felt with curved edges, just like in the illustration above!
Now, Pogorelov’s process also applies to nets of figures with more than 2 faces! In particular, we can reuse the net of the cube, but with rounded squares rather than actual ones!
Note that, just like in Numberphile’s video, angles of a corner cannot add up to more than 360°, otherwise it’d be impossible to fold the net. In the case of the cube with rounded squares of the figure above, since all squares are identical, and since three of them meet at each corner, each angle must be at most 120°.
Brazuca
Finally, we can talk about Brazuca.
Exactly! Now, the roundedness of faces is more complex than in our figure above, but in essence, the principle remains the same. That’s why I said that Brazuca is a cube!
And when we glue this net, faces naturally slightly round as follows:
Adidas has done an amazing job! To avoid pointy corners, they made sure that the angles of the corners of the square-like panels are 120°. Therefore, the angles at corners add up to 360°… which makes corners flat! You can see it in the figure below:
At this point, let’s recapitulate by exploring the geometries of all football balls of History. In fact, let me let Marc Chamberland do that for me in this awesome video of his youtube channel Tipping Point Math:
Thurston’s Octahedron
Interestingly, Adidas’ clever trick to design Brazuca was already studied years ago by William Thurston, who died in 2012. Thurston was probably the greatest topologist/geometer of the 20th Century. He pioneered so-called low-dimensional topology, and famously stated the important geometrization conjecture. This conjecture that generalizes the Poincaré conjecture, and was proved by the eccentric Gregori Perelman in 2003. Roughly, this conjecture lists all possible geometries of our universe.
Thurston famously designed a similar approximation of spheres by a regular polyhedron with curved edges. However, while brazuca is a rounded cube, Thurston envisioned a rounded octahedron, which we’ll merely call Thurston’s octahedron.
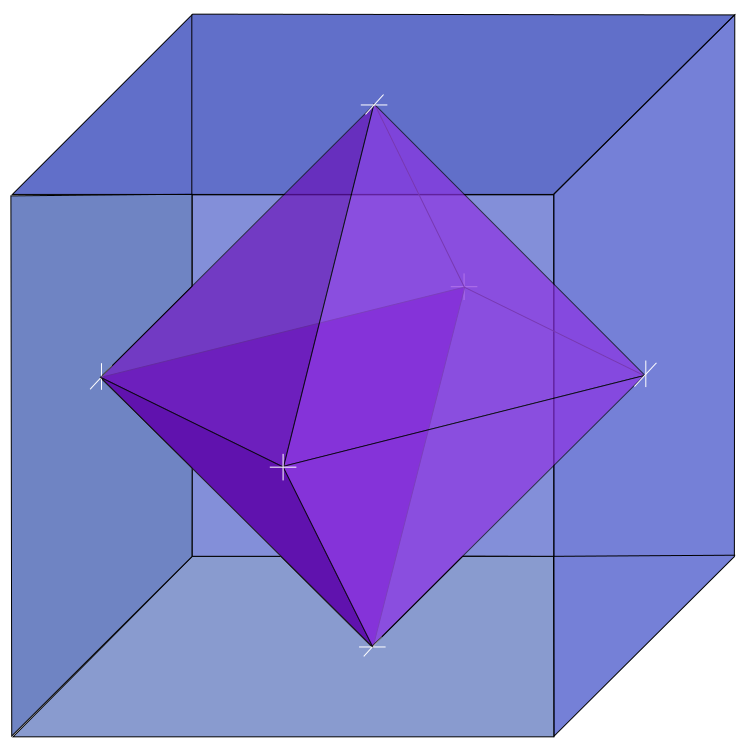
The octahedron is one of the Platonic solids. It is the dual of the cube. This means that it is obtained by linking the centers of the faces of the cube, as displayed below:
As you can see on the figure above, the octahedron has 8 faces that are equilateral triangles, and each summit joins four triangles. Since the angle of a corner of a triangle is 60°, the sum of the four angles at a summit equals 240°.
Exactly! Below are the faces he designed:
Hehe… Here’s what we get:
As you can see, each corner is made of 4 angles of 90°. Just like you predicted!
Gaussian Curvature
Both brazuca and Thurston’s octahedron are in fact mere (very good) approximations of a sphere. With recent progresses of modern mathematics and geometry, a natural question to be asked is whether we can have an exact construction of a sphere by gluing flat faces.
The answer is no. There is a theoretical limitation to producing a round solid using flat sheets of material. And it has to do with one of the most important concept in mathematics History, invented by the Prince of Mathematics, the great, great Carl Friedrich Gauss. This concept is now known as Gaussian curvature.
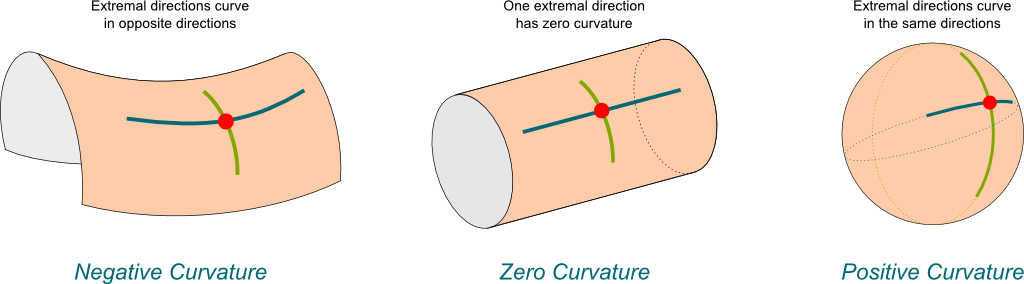
It’s not that complicated. The Gaussian curvature takes a value at each point of the surface, depending on how the surface curves around this point. In particular, it will focus on the two directions along which the surface curves the most.
Sure! Let’s look at a cylinder.
On a cylinder, the direction that curves the most is the rotating direction, while the direction that curves the least is the main direction of the cylinder. Now, the Gaussian curvature is the product of these two curvatures. In the case of the cylinder, the least curvature (the blue in the figure) does not curve at all. So it has zero curvature. Thus, the Gaussian curvature is zero too. As counter-intuitive as it sounds, according to Gauss, cylinders have no curvature.
The sphere has the particularity of having the same curvature in all directions. Plus, at any point and along two perpendicular directions, the sphere curves in the same direction. Therefore, the sphere has a positive curvature. There are also surfaces with negative curvatures, whose extremal curving directions curve in opposite directions, as displayed below:
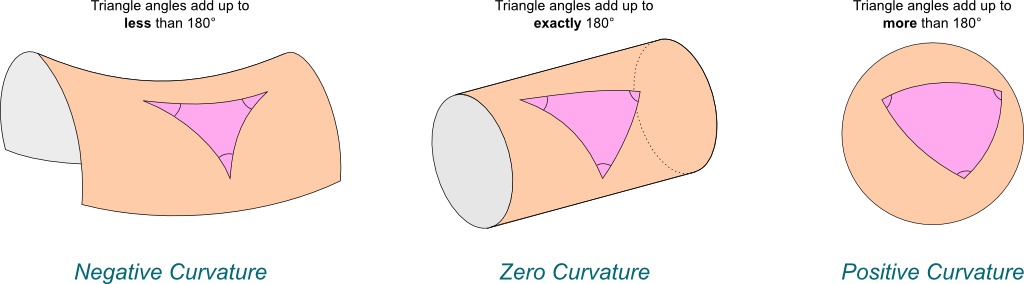
I’m nearly there. One last thing I need to tell you about is one of the most beautiful theorem of Gauss. In fact it is such a beautiful theorem that Gauss called it Theorema Egregium. This is latin for “Remarkable Theorem”. This Theorema Egregium states that this curvature can be computed by mere length or/and angle measurements made directly on the surface. One famous illustration of that corresponds to looking at how angles of triangles add up, as displayed below.
This theorem is crucial. It says that when surfaces are bent (but not stretched!), because measurements of lengths and angles on them remain unchanged, their Gaussian curvatures should not change either. In technical terms, the Gaussian curvature is invariant under isometries. A brilliant illustration of that is the following beautiful justification of how to best eat pizzas, as explained by Colm Kelleher on TedEd:
Finally, we can get back to balls and polyhedra. The mathematical limit unveiled by Gauss’ Theorema Egregium comes from the fact that balls have positive Gaussian curvatures everywhere, while flat sheets have zero Gaussian curvature everywhere. So, if you take a polyhedron with curved edges, the trouble originates from the fact that flat faces are mathematically unable to represent the positive curvature of the sphere they are supposed to coincide with. Therefore, it is mathematically impossible for a volume with (a finite number of) flat faces to exactly represent a sphere.
The felt material of the tennis ball is very stretchable, and that’s why the mathematical limit does not apply directly to it. But in fact, if you cut a tennis ball along the curved line that glue its two contours, then you’ll see that the originally flat contours are no longer flat. They have been curved by their being glued to the sphere they encircle.
Interestingly, Thurston’s octahedron and brazuca both have the property of never yielding any large flat area in their faces. In some sense, the zero Gaussian curvature of flat faces can never add up too much to strongly differ from the positive Gaussian curvature of spheres. Instead, the missing positive Gaussian curvatures of the flat faces appears in the discontinuities appearing along edges. Having long curved edges enable to spread these discontinuities though.
I know! Let me recapitulate (and have you learning more!) with this brilliant extract from the Larouche PAC Riemann Project, presented by Jason Ross. As you’ll see, the fundamental concept of Gaussian curvature is the seed of our present understanding of space (and time), through Riemannian geometry and Einstein’s general relativity:
Let’s Conclude
How amazing is brazuca? I wouldn’t have thought that it was so related to fundamental mathematical concepts like Platonic solids, Pogorelov theorem, Thurston’s octahedron and Gaussian curvature! In particular, I find it mind-blowing that brazuca is just a cube with curved edges! Here’s a video on the Science4All Youtube channel that I made on the brazuca and its predecessors:
Frankly, I don’t think I’m exaggerating as I claim that brazuca is just as amazing as the 2014 world cup… Wait! I take it back. This world cup is legendary!







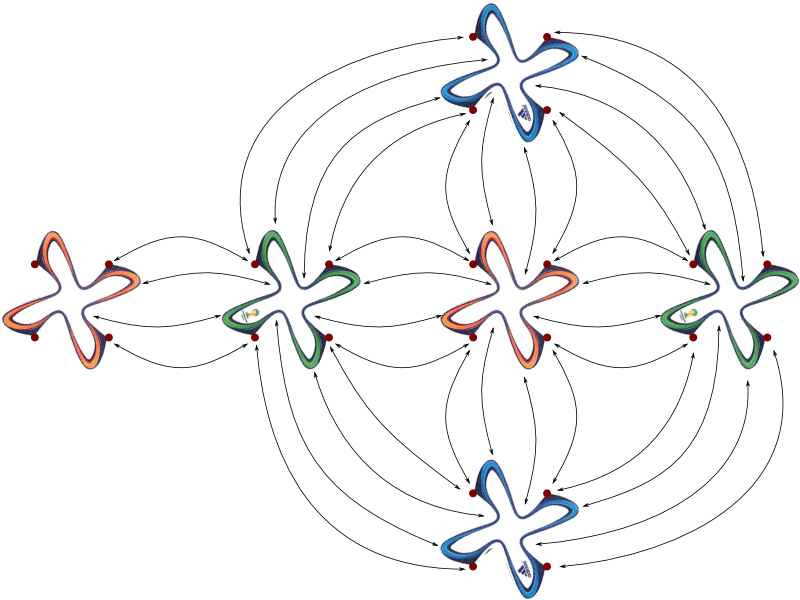



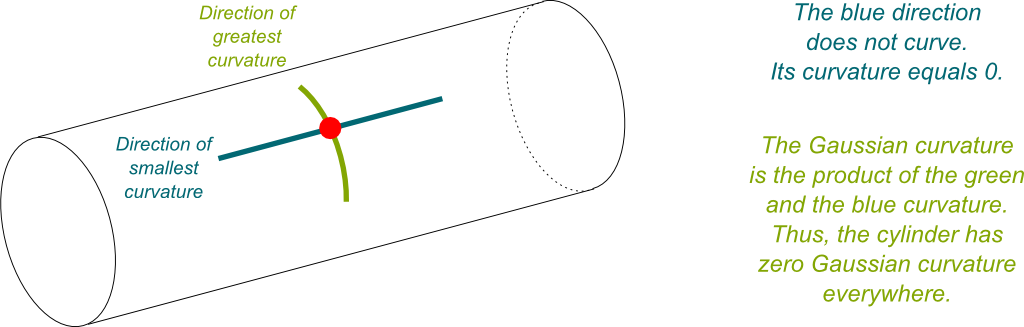

Leave a Reply