In the articles here at science4all, the goal is to expose you, the reader, to areas of higher-level science and mathematics that are useful for understanding our planet and the broader universe. I have previously written (here, here, and here) about how mathematical developments in geometry provided a framework for important discoveries in 20th century physics.
In the next three posts, we’ll take a look at another area of mathematics that is actively being developed by both theoretical and practical scientists: dynamical systems, which leads to the study known popularly as “chaos theory”, as well as “fractals”, which are beautiful, mathematically rich, and useful for understanding the universe.
This is a computer-generated image of a fern, an example of the fractal geometry of nature (via robbritton.com).
The study of dynamical systems provides a natural framework to understand phenomena such as the spread of diseases, the development of social connections on networks such as Facebook, the proliferation of Apps for web-linked phones, and so forth. We’ll start off with a glimpse into the mathematics behind some of these dynamical systems, and in the upcoming posts build a mathematical theory that allows for a superior way to understand the increasingly complex life of the 21st century.
Introduction to Dynamical Systems
A dynamical system is one which evolves through time in such a way that is completely determined at each point in time by a specific rule or pattern. One example is the orbits of planets around the sun. In the GIF picture linked below (click on it!), the planets orbit the sun, which in turn orbits Galactic Central Point.
At any given instant, the behavior of a planet is determined by its current location, the location of other celestial objects such as the sun, and its current velocity. Its previous location, and what happened to it in the past, are irrelevant. All that is necessary to determine its future behavior is its current state, and the state of other astronomical objects it interacts with. Using the laws of physics, we can then describe the behavior of its orbit around the sun – and likewise, the sun’s orbit through the galaxy.
A few other examples of dynamical systems:
Cellular growth
The weather
Water flowing through a system of pipes
Stock market prices
Gossip spreading through a social network
Each of these systems evolves in such a way that is completely determined by the current state of the system and a set of rules, perhaps given by physics, biology, economics, psychology, or fluid dynamics.
The rules governing the evolution of the stock market are not fully understood; someone who understands the market’s behavior stands to make a great deal of money off of it. Still, we regard it as a dynamical system because its future behavior is determined by the current state, together with a set of (complicated) rules involving economics, human psychology, and other scientific areas.
Some concrete examples
Let’s take a deeper look at the first of these examples of real-life dynamical systems, which is a bit easier to understand than the stock market.
Cellular growth
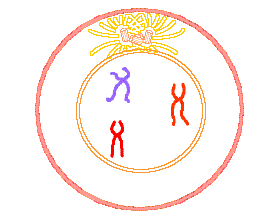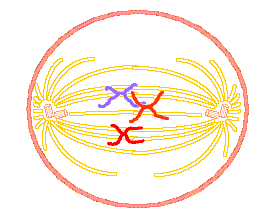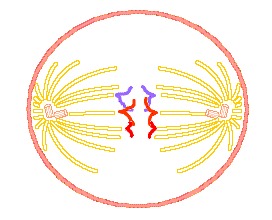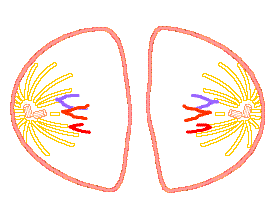
Biologists studying cellular growth note that cells reproduce themselves by a process called mitosis – essentially, a cell reproduces by dividing into two cells, each of which is identical to the original. After one step of mitosis, there are two cells – the two cells the original one has created. Check out this gif image of the mitosis process (from here).
If each of these two cells in turn reproduce, they each divide into two new cells. At this step, there are four cells in the population. If these four cells reproduce, they each divide into two cells, resulting in a total of eight cells. At each step of cellular division, the total number of cells doubles. Let’s plot this out to get a picture of this type of growth.
This example is slightly oversimplified, as there is also the possibility that some cells will die off, or that some cells will not reproduce when the cellular population becomes crowded, but it illustrates the key features of a dynamical system.
At any given instance, the number of cells in the population is entirely determined by (1) the number of cells currently in existence, what dynamical systems theorists call its “state”, and (2) the rate at which they grow (or possibly die off), the “rule” that determines how the cellular population evolves.
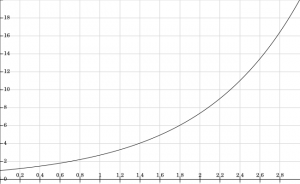
Mathematically, we can model the population’s growth using the differential equation $\frac{\mathrm{d} \textup{P}}{\mathrm{d} \textup{t}} $=$ \textup{P}(\textup{t})$, where P is the current population at a given time t. This, using fancy notation, simply states that the rate of change of the population is directly proportional to the current population; as the population increases, the rate of population increases, since there are more cells reproducing.
A solution to this differential equation is given by the exponential equation $\textup{P}(\textup{t})$=$\textup{C}e^{\textup{t}}$, where C is some constant.
A graph (made using FooPlot) of this population model is given as follows:
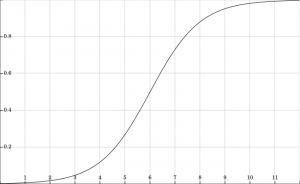
A more accurate model for the cell population’s growth is given by the logistic equation: $\frac{\mathrm{d} \textup{P}}{\mathrm{d} \textup{t}} $=$ \textup{P}(\textup{t})(1-\textup{P}(\textup{t}))$, which implies that the rate of change of the population increases as the population slowly grows, but as the population becomes crowded, the population’s rate of growth in turn decreases. The point at which the population becomes crowded depends on the carrying capacity of the environment.
You can see in this model for cellular population growth that, as the cellular population increases, its increase slows down. The same will happen for population on the planet Earth, since as the population continues to grow, resources will become scarce, wars will increase, and so forth, making it impossible for the population to continue growing at its current rate.
Spreading gossip
Let’s take a look at a related example of a dynamical system: the spread of gossip. You may have played the game known as “Chinese Whispers”, where a message is passed around a circle of people, who pass it along by whispering it in the ear of their neighbour. By the time the message gets around the circle, it inevitably becomes distorted, with hilarious results.
In a typical gossip situation, however, messages tend to withstand distortion, since mistaken gossip quickly gets corrected. If John isn’t dating Sue, for example, any gossip suggesting that “John is dating Sue” will quickly get corrected. This is one central property of gossip: it’s an effective means of transmitting information within a social network. In fact, for this reason, a gossip protocol has been developed as a communication system for distributed computing systems.
A second attribute of gossip is its rapid spread. Once gossip starts, it moves around like a virus. In fact, the models commonly used to understand the spread of gossip are based on those used to understand the spread of viruses such as influenza.
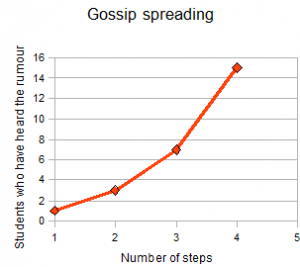
You may recall being a school student – or you may be in school at the moment – when the slightest hint of, say, a male and female student going on a date, quickly spreads throughout the student population. Let’s think about why this is. If one student hears that the couple are “going out”, and tells two of his/her friends, then a total of three students now know that the couple is dating. If each of those two friends tells two more friends that the couple is dating, then four new people know about the relationship. If each of those four people who have learned of the relationship in turn tells two of their friends about the relationship, then eight new people know about the relationship.
After just three steps of sharing information about the relationship, a total of 1+2+4+8=15 people now know about the relationship.
You can experiment with a Java applet modelling gossip spread here. Note how the gossip spreads quickly at first, but then slows down as more and more members of the population have already heard the message.
Perhaps you can see a parallel between the two dynamical systems we’ve seen: gossip spreading and cellular growth. You can probably imagine how, as a piece of gossip spreads throughout the student body, its rate of spread slows, as more students hear about it. The spread of gossip and the growth of a population of cells behave operate according to similar underlying mathematical principles.
In fact, there are even more accurate models for gossip spread, which also help to model the spread of diseases such as influenza. This is one thing we find over and over in different areas of mathematics: the same type of mathematical model, or way of thinking about a real-world problem, applies to many apparently disparate real-world phenomena. The spread of gossip and the spread of a disease like influenza happen in very similar ways, as you can see in this NIH image of a man sneezing.
Propagation of information in networks
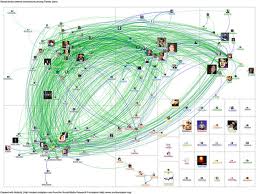
Graph theory provides a natural framework in which to model dynamical systems such as gossip spread and disease propagation. Take a look at this picture, which depicts Facebook users as nodes in a graph, and connections between them as edges between the nodes.
Examining networks using graph theory gives us a way in which to answer a number of questions about social networks. For instance, there is a well-known statement, the “six degrees of separation” idea, that any two people on the planet are connected by at most six pairs of mutual friends. Check out this documentary for more on this question:
Using graph theory, we can also answer some questions about the question we’re interested in – the rate and manner in which gossip spreads.
A mathematical model of gossip spread
In a social network, the rate at which gossip spreads is determined by a number of factors. We previously assumed that gossip would spread evenly throughout the population, ultimately reaching every member in the population. In a 2010 paper, the researchers Shaw, Tsvetkova, and Daneshvar noted that the spread of gossip can actually change the sort of relationships people have with one another, and thus change the structure of the social network. This implies that our relatively simple exponential and logistic models, discussed above, are too simplistic, as they don’t account for the fact that gossip can change the connections of a social network that engages in gossip.
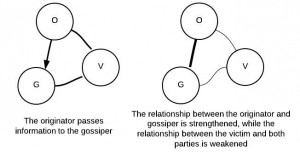
In particular, they noted, in a typical situation involving gossip, two friends (the originator and the gossiper) engage in gossip about a third person (the victim). The originator and the gossiper, having shared this information, will tend to have a stronger friendship as a result of this act, but the relationship between the victim of the gossip and the two gossiping friends will be weakened.
Gossip effects the level of trust between individuals, and this in turn effects the way in which gossip is propagated.
Putting this into mathematical terms: suppose a connected social network – one in which every person is friends with every other person – has m individuals. Suppose also that each of those friendships has a “strength” of w, with 0<w<1, then on average, the strength of each link in the network will approach $w^{(\frac{1}{L})^{n(1-\frac{2}{m}))}$*$L^{(\frac{2n}{m})}}$, or in simple terms, $w^{L^{\frac{-n(m-2)}{m}}}$.
This implies that the network's behavior is governed by m, the number of individuals in the network. If m<4, then the strength of the links in the network will decrease to 0. If m=4, the strength of the links will remain constant, and if m>4, the strength of the links in the network will increase to 1.
This model suggests that, for a network with more than 4 people, gossip, even negative gossip, tends to strengthen the relationships in the network.
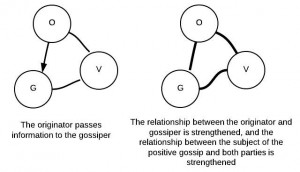
Gossip can also have the opposite effect on relationships between the subject of the gossip and its spreaders. If the gossip is positive, say “Jenny received a perfect score on the math test”, then anyone who spreads this gossip will presumably have a positive reaction from Jenny, resulting in a stronger relationship. We can depict this in the following way:
In both of these cases, negative and positive gossip, gossip ultimately strengthens the relationships within the network, assuming the network is sufficiently large. This, perhaps, explains why gossip is so widespread among humans: it helps strengthen relationships in a social network, regardless of the actual content of the gossip. The simple act of exchanging information in a network helps to strengthen that network.
The weather
To wrap this post up, let’s take a look at a couple of final dynamical systems that exhibit a property commonly known as “chaos”.
The weather operates as a dynamical system: its behavior is governed by (1) its current state, and (2) a system of rules, based in physics and chemistry. A couple of examples of such rules: a high pressure region tends to produce clear skies, while conditions over the Atlantic in the summer tend to produce hurricanes.
The weather has a special property known as “sensitivity to initial conditions”: if the initial state of a weather system is very slightly perturbed, this can result in profound changes in the overall system. The popular image for this is the observation that a butterfly flapping its wings in China can cause a tornado in Texas. This is sometimes known as the butterfly effect.
An easy way to picture the butterfly effect is by looking at the behavior of double pendulums. Check out this video from Guilford College, and note how the two double pendulums behave in wildly different manners when they begin from distinct initial states.
The area of dynamical systems that studies the sort of “untame” dynamical systems of this sort, chaos theory, has become well known in the popular press. Over the next two posts we’ll introduce a mathematical framework that gives us a methodical way to model such complex yet naturally occurring dynamical systems.
To do this, we’ll have to consider a few theoretical dynamical systems, ones that don’t exist in the planet, but instead arise out of “pure” mathematics. Stay tuned!
claimtoken-5159812e6e61e







Leave a Reply