Last summer, I visited the exposition Dynamo at the Grand Palais in Paris. Some of the beautiful art pieces were mind-blowing mathematical objects! I got particularly intrigued by one artwork by François Morellet…
It’s very simple. It consists in superposing 4 grids inclined by angles of 0, 22.5°, 45° and 67.5°. This is what you obtain:
I stood 10 long minutes in front of this painting. Speechless, and deeply puzzled.
Precisely! Given how simple its construction is, I was expecting strong patterns appearing. Yet, all we can see are chaotic unstructured messy lines!
And, then, suddenly, it hit me.
What I was looking at, and what you are looking at, is the geometry of irrational numbers, including and especially the geometry of the square root of 2! In this article, I’ll show you what this irrationality means and why it generates such a chaotic picture. This will also give a Historical key argument to the existence of irrational numbers. After discovering these irrational numbers, mathematics has been building up more and more sophisticated classes of numbers I’ll then get to.
Irrational Numbers
As you’ve probably learned it a long time ago, many numbers can be written as fractions. For instance, $2/3$, $7/5$, $241531/2353$, but also $3=3/1$. These are all fractions. In number theory, we call them rational numbers, as they can be expressed as a ratio. By opposition, irrational numbers are…
Exactly!
Back in Ancient Greece, the Pythagorean philosophers believed that all numbers were rationals. They could not stand the idea that there were numbers which couldn’t be written as fractions. But, Hippasus of Metapontum discovered that $\sqrt{2}$, the square root of 2, was in fact not rational. As the story goes, the Pythagoreans drowned him for this act of treason against his own community! This is what Marcus du Sautoy explains in this extract from the wonderful BBC show The Story of Maths:
Humm… let’s get to that later…
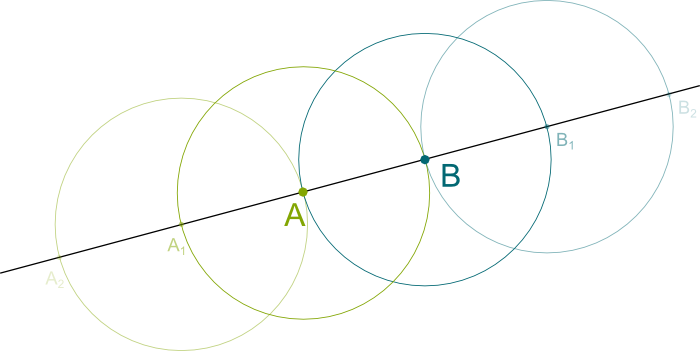
Let’s take a simpler version of Morellet’s painting. Namely, let’s remove the grids rotated by 22.5° and 67.5°. If we only keep the initial grid and the one inclined by 45°, here’s what we get:
Once again, except for the axial symmetries along the lines passing through red point where the two grids meet, there is no pattern appearing. In fact, as I’m staring at this patternless image longly, I’m getting dizzy…
Amazingly, there is so little pattern that I can assure you that the two grids will never ever meet again. In fact, if you look at a large number of intersections relatively to each of the green squares, they will seem randomly and uniformly distributed! And the cause of that is precisely the irrationality of $\sqrt{2}$!
Let’s consider that all squares of the grids have a side of length 1 unit. To make matters simple, let’s only focus on the horizontal green line which goes through the red point, and let’s keep track of the intersections of the blue grid with this green line on the right of the red point. At the next intersection, the green line will have been the diagonal of a blue square. But as Marcus du Sautoy said, and as you can prove it using Pythagorus theorem, the diagonal of a square of side 1 is…
Exactly! And this means that the next intersection occurs $\sqrt{2}$ units away from the red point. But this pattern keeps repeating itself. The second intersection will occur $\sqrt{2}+\sqrt{2} = 2\sqrt{2}$ units away from the red point. Eventually, the $n$-th intersection occurs $n\sqrt{2}$ units away from the red point. But for the $n$-th intersection to be the intersection of the two grids, this intersection must occur at a whole number of units away from the red point. So, $n\sqrt{2}$ must be an integer $m$. But this can’t happen, as it would imply that $\sqrt{2}=m/n$, which would contradict…
I know! And you could go further and prove that the irrationality of $\sqrt{2}$ implies that the relative position of the intersections of the blue grid with the horizontal line with regards to green squares is dense.
In fact, in the whole picture, if it is large enough, it means that if you pick randomly an point of the blue grid, then it will be uniformly distributed in the area of the green square which contains it! These facts describe mathematically how profoundly messy and chaotic Morellet’s brilliant artwork is! And this is why I assert that it displays the irrationality of $\sqrt{2}$…
Arg… I thought (hoped?) you had forgotten about that! Well, I’m feeling a bit lazy, so I’ll let the professors of Numberphile explain that, along with some other pretty cool facts about $\sqrt{2}$:
Well, he’s a bad boss! But, fine… Below is the proof. But don’t worry if you don’t understand it, it won’t be relevant for this article!
Constructible Numbers
While the Pythagoreans argued that irrational numbers don’t exist, Hippasus would argue that $\sqrt{2}$ does, because we can draw it. Nowadays, this argument doesn’t seem relevant as we have got used to dealing with so many more irrational numbers. Yet, it’s a crucial one in the History of mathematics. In particular, the expression squaring the circle comes from the fascinating concept of constructible numbers.
It’s a number that can be constructed by using only a compass and straightedges.
We start with two points in the plane. Then, to construct new points we must follow the three following rules:
- Any new point we construct needs to be the intersection of two lines, two circles or a line and a circle.
- Lines are drawn with the ruler and must pass through two points we have already constructed.
- Circles must be centered on points we have already constructed, and their radius must be the distance between two points we have already constructed.
We call 1 the distance between the two initial points we had. Then, a number is constructible if we can construct two points such that the distance separating them is the number in question.
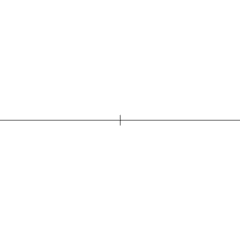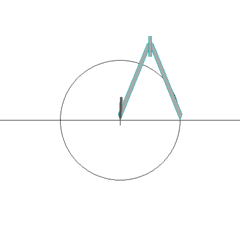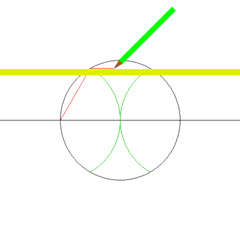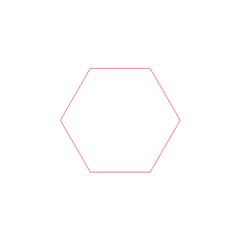
Sure! Let’s start by constructing all integer numbers. Call $A$ and $B$ the two initial points in the plane. Now, let’s draw this line with the ruler. Then, using the compass, we draw circles of radii 1, centered on $A$ and $B$. The new intersections we then obtain are points $A_1$ and $B_1$. Both are on the line $(AB)$. One is at distance 1 of $A$, and the other at distance 1 of $B$. By now repeating this procedure with circles of radii 1 centered on $A_1$ and $B_1$ and so on, we can in fact construct all points on $(AB)$ at an integer distance from $A$ and $B$. This is what’s done below:
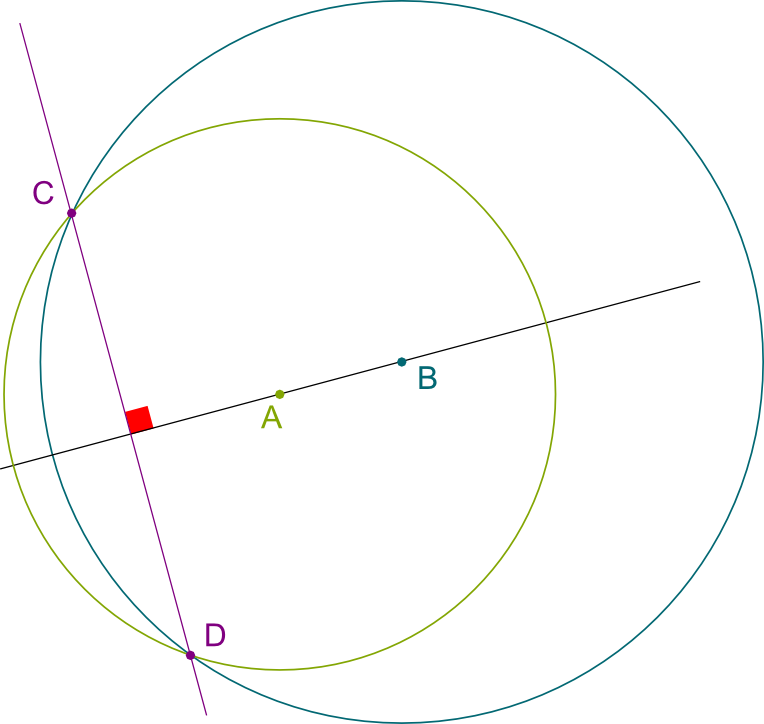
Hehe… This is getting interesting! Let’s first show you how to construct a perpendicular to a line that goes through a certain point. This will be helpful to construct $\sqrt{2}$!
Consider a line we have already constructed. This means that there are two points $A$ and $B$ of this line we have constructed. Let $C$ the point we want the perpendicular to go through. Then the circle of radius $AC$ and center $A$, and the circle of radius $BC$ and center $B$ meet in $C$ as well as in another point $D$. The line that goes through $C$ and $D$ is then the perpendicular we were searching for!
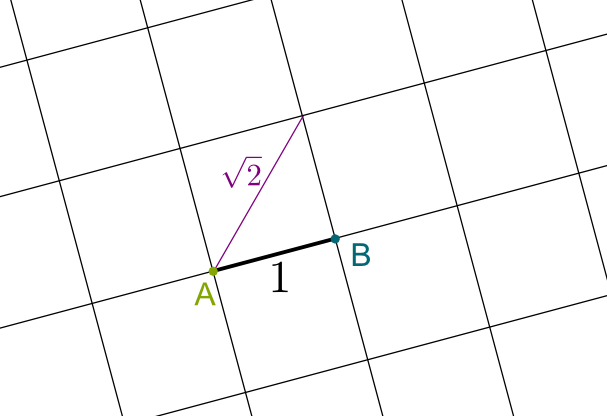
Combining the constructions of integer numbers and of perpendiculars that go through a certain point, we can now construct a grid like the one this article started with, whose squares are of side 1! In particular, any square of this grid has a diagonal of length $\sqrt{2}$… We have just proved that $\sqrt{2}$ is constructible!
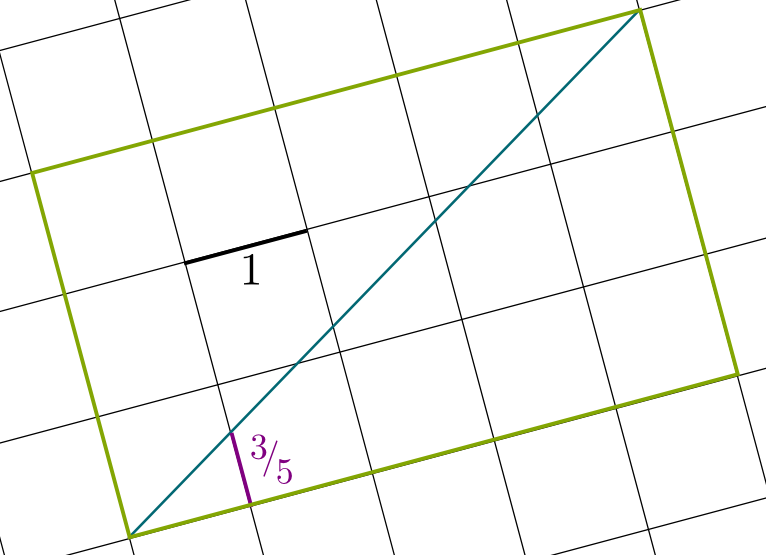
Yes there are! Let’s consider $3/5$ for instance. In the grid, we can consider a rectangle of width 5 and height 3. Once again, we will draw its diagonal. This diagonal intersects the first of the 5 vertical lines at height $3/5$! And if you want any rational number $p/q$, you simply need to do this for a rectangle $p$ by $q$ instead!
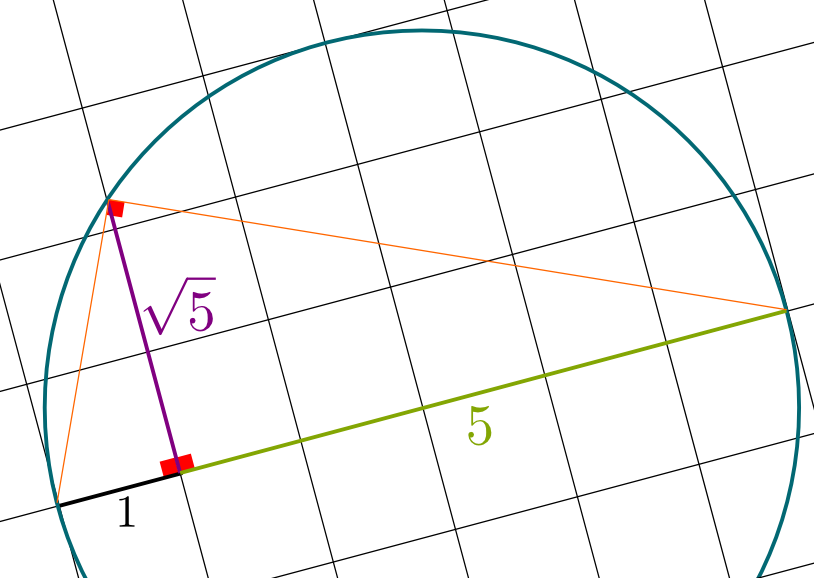
Yes! For instance, to construct $\sqrt{5}$, consider a circle of diameter $5+1=6$, centered on a point of the grid. Then, the intersection of the vertical line at distance 1 from the intersection of the horizontal diameter with the circle defines a height of $\sqrt{5}$. And once again, to construct any $\sqrt{n}$, we just need to take a circle of diameter $n+1$! This is what’s done below:
In fact, this construction shows that we can construct the square root of any constructible numbers. So, not only is $\sqrt{5}$ constructible, but so is $\sqrt[4]{5} = \sqrt{\sqrt{5}}$, as well as other more complicated numbers such as $\sqrt{\sqrt{2}+\sqrt{3}}$!
That’s a great question! Historically, the regular heptagon, the regular polygon of 7 sides, was the first polygon to be shown to be non-constructible!
I know! This is known as the Gauss-Wantzel theorem. And it implies that the numbers associated to the heights of the points of a regular heptagon of side 1 are non-constructible! More generally, the beautiful Galois theory has emerged around the 1830s to give an amazing insight into the constructibility, algebra and geometry of numbers! Using it, it’s relatively simple to then show that $\sqrt[3]{2}$ is non-constructible! Unfortunately, I won’t have time to get into it here… But I’ll definitely write about it soon!
It took a while to figure it out, but the most important number of mathematics, $\tau$ (and not $\pi$!), is non-constructible! This non-constructibility corresponds to the impossibility of squaring the circle, as explains by the awesome James Grime on Numberphile:
Transcendental Numbers
Most greek scholars considered that numbers needed to be constructible to exist. But the invention of algebra by Muslim scholars then showed that numbers can be defined in other ways than with a compass and a straightedge! In particular, that’s the case of $\sqrt[3]{2}$. This led mathematician to define a new class of numbers, called the algebraic numbers.
An algebraic number is a number constructible by a finite number of algebraic manipulations. More precisely, it’s a number which can be brought to 0 with a finite number of multiplications and additions. This is what’s brilliantly explained by Simon Pampena on Numberphile:
So, as explained by Simon, another way of defining algebraic numbers is by considering them as the solutions of polynomial equations. These are equations of the form $a_n x^n + a_{n-1} x^{n-1} + \ldots + a_1 x + a_0 = 0$, where the coefficients $a_i$ are integers. For instance, when $n=3$, $a_3=1$, $a_2 = a_1 =0$ and $a_0=-2$, the polynomial equation becomes $x^3-2=0$. Since $\sqrt[3]{2}$ is a solution, it is an algebraic number.
Amusingly, no. This equation has other solutions, namely $\sqrt[3]{2} e^{i\tau/3}$ and $\sqrt[3]{2} e^{2i\tau/3}$.
Galois theory defines these other solutions as the conjugates of $\sqrt[3]{2}$. This means that, whenever we replace $\sqrt[3]{2}$ by any of the two others in algebraic equalities, the equalities still hold. Thus, from a purely algebraic viewpoint, that is, if we only consider additions, multiplications and equalities, there is no difference between $\sqrt[3]{2}$ and its conjugates.
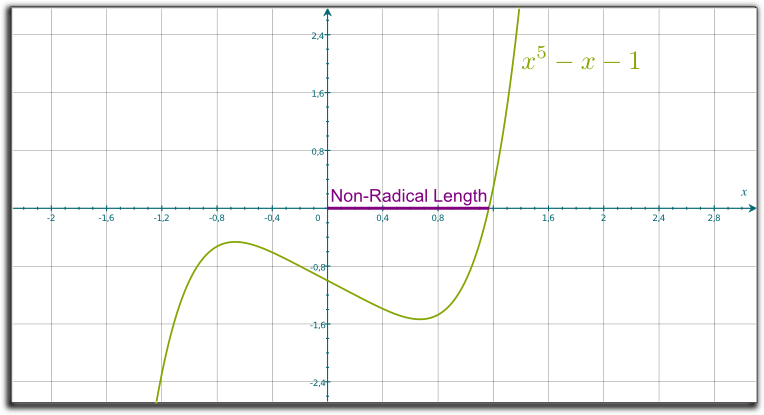
Actually, no. A famous surprising result of Galois theory is that most algebraic numbers can actually not be written with radicals. In particular, for equations of degree at least 5, there is no way to write the solutions as a combination of $n$-th roots of the coefficients. And this is the case of the only real number solution to the equation $x^5-x-1=0$, which is about $1.1673$, and is displayed in the following figure:
Indeed, it is not. Nor is $\tau = 2\pi$. For this reason, it is called a transcendental numbers. The other important example is Euler’s constant $e \approx 2.7$. Numbers constructed from $\pi$ and $e$ are often transcendental too. In particular, Hilbert’s 7th problem has been solved in 1934 by the Gelfond-Schneider theorem. It states that if $a$ is algebraic different from 0 and 1 and if $b$ is irrational algebraic, then $a^b$ is transcendental.
Computable Numbers
Crucially, transcendental numbers are not constructible geometrically nor algebraically…
Hehe… Great question! Most are in fact defined analytically. For instance, $\tau$ is typically defined as one of the solutions of the non-polynomial equation $\sin(\tau)=0$. More simply, transcendental numbers are often defined as infinite series like $e = \sum 1/n! = 1+1/1+1/2+1/6+1/24+\ldots$. In fact, the invention of infinite sums has led to a boom of constructed numbers in mathematics.
Historically, the first number to be proved transcendental is the Liouville constant $\sum 10^{-n!}$. Another more recent example is the Champernowne constant $0.123456789101112…$, which can be precisely written using an infinite sum.
Sort of. In 1936, British mathematician Alan Turing defined computable numbers as numbers which can be approximated as closely as desired by a finite terminating procedure. Infinite series $\sum a_n$, whose speed of convergence we can control and whose general terms $a_n$ are all given by the same finite terminating procedure, are computable.
Yes! Historically, the first non-computable real number envisioned was introduced by French mathematician Émile Borel in 1927. Around the same time as Kurt Gödel, Borel noticed that there is only a countably infinite amount of yes-no questions we can ask with words or mathematical symbols. Thus, Borel imagined listing them all, and devised a single real number to include all the answers of all yes-no mathematical questions: The $n$-th decimal digit of this number in base 2 would simply be 0 if the answer of the $n$-th question is no, and it would be 1 otherwise.
Yes! Isn’t it amazing? Unfortunately though, this number is still hard to define as we need to come up with an actual way of listing all the mathematical questions. But, building up on this idea, Gregory Chaitin defined uniquely and unambiguously a similar kind of number, now known as Chaitin’s constant, and commonly denoted $\Omega$.
Roughly speaking, $\Omega$ is real number between 0 and 1 which represents efficiently all the information about the termination of an algorithm for some randomly chosen input. It thus depends on the algorithm we consider. But for almost all algorithms, this number is non-computable.
To have an approximation of $\Omega$, we need to test whether inputs of small lengths have the algorithm terminating. Yet, this corresponds to solving many halting problems, which have been proved to be non-computable!
No. And that’s because all algebraic are computable!
Yes! $\Omega$ is a definable number, which means that it can be defined with a finite number of words or symbols in a mathematical theory. Thus, definable numbers contain by definition exactly all the numbers we will ever be able to construct.
Let’s Conclude
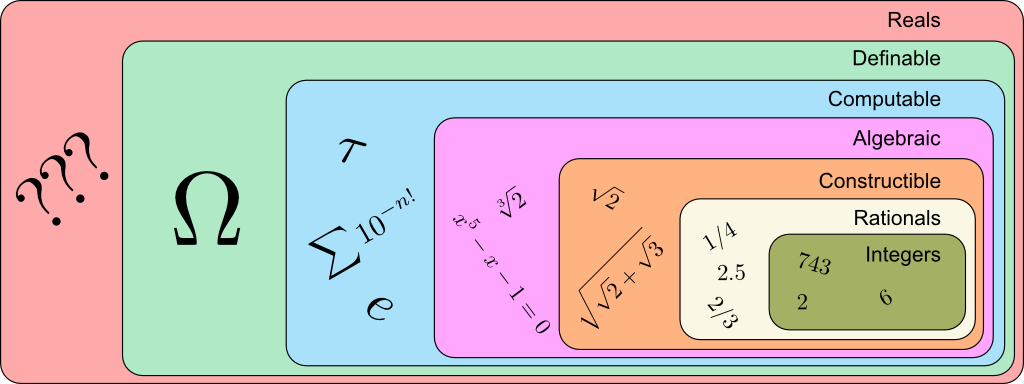
To recapitulate all we’ve talked about, here’s a Venn diagram which depicts all the classes of numbers we have discussed in this article:
As you can see, the realm of numbers mathematics can define has kept increasing, using sequentially geometric, algebraic, analytic and set theoretical arguments! Amusingly though, the set mathematicians are the most familiar is none of these. Indeed, the numbers mathematicians most often refer to is the set of real numbers, which, for the overwhelming majority, are actually fundamentally non-constructible…
Finally, I’ll conclude with a few words about what it means to be a mathematician. Last summer, I visited the Grand Palais with my mom. She’s awesome (obviously!), but she didn’t get as puzzled as I did when facing Morellet’s artwork. And this made me realize what the most important quality of a mathematician was: It’s the ability to be deeply intrigued, almost obsessed, by patterns. In some sense, this is the best definition I know of what a mathematician is.



Leave a Reply