I am not always excited by seminars I get to attend. But a few weeks ago, one seminar got me very excited. The presenter, Yang Cai, had solved the auction design problem. That’s the problem of how best to sell. Here’s one funny illustration of this selling problem:
In this article, I will not dwell on the solution by Cai and his co-authors — because their result is in fact more general than the auction design problem, and I’ll write about it in another article! Instead, I’ll tell you about what I knew before I listened to his talk and read his papers. As you’ll see, it was already pretty cool. But a bit frustrating…
The Auction Design Problem
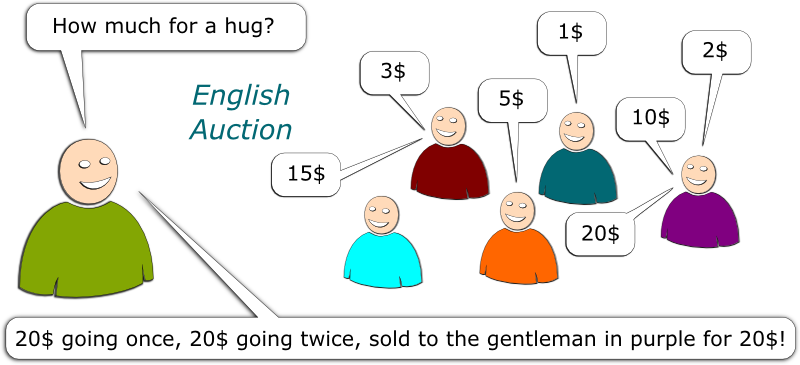
Let’s start with the example of the video. After all, it’s the most classic of all auctions. It’s the one you were probably thinking about when I told you about the auction design problem. It’s sometimes called the English auction.
Let me tell you about the auction design problem first. Imagine that a seller has one good to sell to potential buyers. As the commercial above exemplified it, the does not need to be material. It can be a help to jump out of a building more safely, or rights to operate some frequencies for telecommunication, or to have your ad displayed on a very visible platform. I’m mentioning these latter two, because they are literary billion dollar auctions — Google wins around 96% of his money through auctions via Adwords. When billions of dollars are at play, you can imagine that your auction design needs to be optimized.
I guess I should answer your first question now.
In the English auction, a good is set at a certain low price. Potential buyers then bid higher and higher prices. The last bidder, who is also the one with the highest bid, then wins the good, and pays it at the price of his highest bid. It’s the one you see in many painting auctions and in many movies. You know? With the famous: “200 dollars going once, 200 dollars going twice, sold!”
The English auction is not that bad. Eventually, the good will be sold to the buyer that values it the most. But to get it, he’ll only need to bid slightly more than the highest bid of other potential buyers. Thus, the buyer will not sell it at the highest price you could possibly dream of, that is, the price at which the buyer actually values the good.
Sure, just sell the good at the price at which the highest bidder values it!
You’re perfectly right! In fact, that’s precisely the difficulty of the auction design problem. To best sell, the seller needs some information that only the (highest) bidders possess. Yet, these bidders have all the incentives in the world not to reveal it to you — when you’re buying a car, do not tell the seller how much you’re really willing to pay to buy it! Instead, the bidders will do whatever they can to get the good, while paying it as cheaply as possible and definitely not more than how much they value the good.
Exactly! Now, let’s see what these strategies are in different simple auctions.
Example of Auctions
One trouble of the English auction is that it can be pretty long. Plus, the crowd of buyer needs to be quite calm, so that the seller can hear the bids. Yet, that was not the case during the epic tulip financial bubble.
It’s the first financial bubble in History! Back in the 1600s in the Netherlands, where banking was invented, the recent importation of tulips quickly became hugely popular. The demand was huge, but the supply was not — growing a tulip takes at least 7 years and nobody wanted to wait. The laws of economics tell us that this leads to the increase of prices. But then, because the prices of tulips were clearly increasing, traders knew they’d better buy a lot today, so that they can sell tomorrow at greater prices. This led to a boom of prices. At some point, a tulip would cost as much as a mansion! This is what’s nicely told in this cool video by Radar:
But as prices would increase every day, how then could sellers determine the prices of their goods, when they were permanently surrounded by noisy undisciplined crowds? The sellers’ preferred solution was the now-called Dutch auction.
The seller would start by a very high price. He would then decrease it until someone claims it.
It’s the great question! A trade-off appears for the bidder when the price is less or equal to what he’s willing to pay to get the good: If he waits, he can get it for a smaller price, but there’s a risk that another bidder would take it away from him. So, there is an information problem. Exactly like in a (first-price) sealed auction.
It’s the one that had Joey Tribbiani unwilling buying a boat, on the classic TV show friends:
In the sealed auction, bidders secretly write down how much they’re willing to pay to get the good. The highest bid then wins it, like in the English auction.
In both case, the bidders’ rational strategy is to bid the smallest price that will secure the good, if the bidder is himself willing to pay that price. If a bidder knew all other bidders’ valuations of the good, this smallest price would equal the highest of others’ valuations (plus slightly more). Interestingly, this outcome is exactly the same as the one achieved by the English auction: The good is eventually assigned to the bidder that values it the most at the price of the second highest bidder.
You’re perfectly right. It’s a bit trickier though, so I’ll get there in a bit! For now, I want to mention one last auction: the Japanese auction.
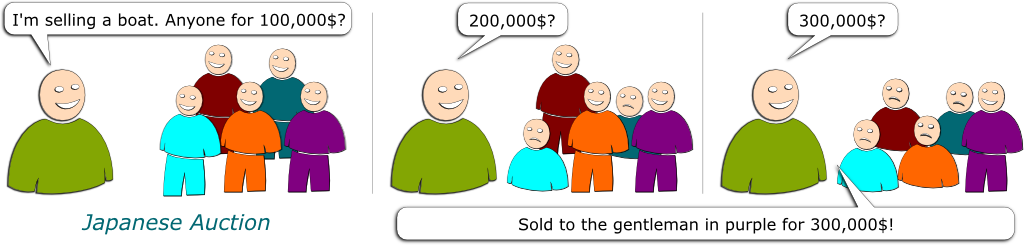
The Japanese auction is a bit of the converse of the Dutch auction, and is pretty similar to the English auction. The seller starts at a low price and slowly increases it. Bidders stand up and only sit down once they are unwilling to buy the good at the current displayed price. The good is eventually sold to the (literally) last man standing.
And this case, the bidders’ rational strategy is…
Exactly! In this Japanese auction, the bidders’ rational strategy is also the one we sort of expect them to play. In other words, the Japanese auction is incentive-compatible, in the sense that we give bidders incentives to bid the way we want them to bid.
The VCG Mechanism
The first person to really theorize auctions was the American economist William Vickrey. This would win him a Nobel prize in 1996. He noticed that all known auctions boiled down, as we’ve seen, to the good being sold to the highest bidder at the price of the second highest bidder’s valuation. So, he figured out, why not do directly a sealed second-price auction?
Just like in the first-price sealed auction I mentioned above, we’re going to ask potential buyers to write down how much they’re willing to pay for the good. Still like in the first-price auction, the good will be sold to the highest bidder. However, this highest bidder will not have to pay the price he bid; he will have to pay the price that the second highest bidder bid.
The advantage of the sealed second-price auction is that it is incentive-compatible. In other words, bidders now have incentives to bid truthfully, that is, writing down how much they’re really willing to pay their good.
No, it won’t. Once again, the outcome will be basically the same as in other auctions: The good will go to the highest bidder at the price of the second highest bidder. And that’s not so bad. At least, the good will go to the person that values it the most. In economist terms, the allocation is said to be socially efficient.
In the case of the auction of a single good, indeed it was not — the English and Japanese auctions do that very well too. But let’s imagine another more complicated kind of auction. Imagine the government wants to construct roads connecting diverse cities, and he wants cities to pay for the roads.
Yes! The outcome of the auction is a choice of road network, and the potential buyers are the different cities. Each city prefers some road networks to others, but will want to pay as little as possible as well. Pricing such a road network becomes much more complicated, as all cities benefit from the road network and it seems that they should thus all pay for it. But some cities will gain more from a certain road network than from another.
It is. It’s really not clear how to best design it. Fortunately, the power of mathematics and the genius of Edward Clarke first and of Theodore Groves later have allowed a surprisingly elegant generalization of Vickrey’s auction to this more complicated general case, which we now call the Vicrkey-Clarke-Groves auction, or VCG mechanism.
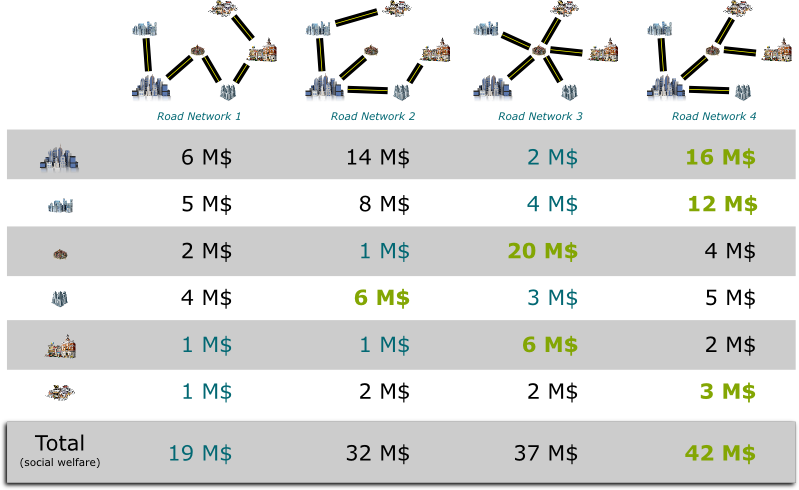
First, we ask each city to reveal how much it values the different road networks.
We then choose to build the road network that the cities altogether value the most: The fourth road network.
That’s the big question. Clarke’s brilliant answer was to have cities paying their negative externalities on the collectivity.
Consider one city called NYC. If it was not there, his bids would not be considered, and thus, the road network chosen by the VCG auction might be different. But if it is different, it means that other cities would be happier without NYC. How much happier they would be is exactly what NYC must pay, according to Clarke.
As you can see in the figure, if the big city was not there, then road network number 3 would have been chosen, as opposed to road network number 4. The value of road network 3 for the other cities would be 35 million dollars, as opposed to the 26 million dollars of the road network number 4 that has been chosen, because of the city’s presence in the auction. Therefore, the negative externality of the big city is 35-26 = 9 million dollars.
Yes indeed! Similarly, the second largest city will have to pay 3 million dollars. Conversely though, other cities do not have to pay anything, as their presence has had no effect on the choice of the road network. Indeed, were other cities not there, the auction would still have decided to go with road network number 4.
I don’t know. The trouble of VCG is that it hardly controls how payments will be made. Its main advantage is to be an (dominant-strategy) incentive-compatible mechanism that guarantees the choice of the socially efficient outcome. So, if you’re a state and want to guarantee the happiness of the people, VCG is the way to go. But if you have also monetary considerations in mind, it may not be that good.
The VCG auction is actually the particular case studied by Clarke of the more general class of Groves mechanisms. Crucially, all Groves mechanisms are still incentive-compatible and socially efficient, but they yield different payments. The key of it all lies in the fact that one’s payment depends in a very specific way on what one bids. What’s good about the VCG auction in particular is that the auction designer never has to give money to any bidder, and that bidders are all happier after the auction (given outcome and payments) than before — this is called individual rationality.
Myerson (1981)
The VCG auction is pretty impressive. But, as a seller, it may be of little interest to you. You may not care about social efficiency. You may prefer money. This is called the revenue-optimization auction design problem. And its study turned out to be an even greater mathematical challenge! While the VCG auction was fully determined in the early 1970s, it was only in 1981 that the giant of mathematical economics, Roger Myerson, would solve the revenue-optimization auction design problem in the case of auctions of a single good. In fact, Myerson’s seminal 1981 paper is what won him the Nobel prize in economics!
It really is! In fact, it’s too complicated for me to tell you about the details of Myerson’s many insightful theorems. I’ll only tell you about his two most important theorems. The first is an astounding result. It is called the revenue equivalence theorem.
Roughly, it asserts that the seller’s expected revenue is fully determined by the allocation rule of the good. In particular, all the auctions we’ve discussed so far all end up giving the good to the person who values it the most. Thus, they all have the same allocation rule. Therefore, thanks to Myerson’s revenue equivalence theorem, we can assert that they are all revenue-equivalent.
I know it would seem so. Even weirder, some bizarre auctions, like the all-pay auction where bidders need to pay their bids no matter what, are revenue-equivalent to the English auction! Personally, I was deeply surprised by Myerson’s result — and still kind of am!
It lies in the features of the Bayesian setting, and, more specifically, in the necessary properties of so-called Bayesian-Nash equilibria in single-good auctions. It’s hard for me to give you a deep insight into what’s going on here, but roughly, the allocation rule and the Bayesian-Nash equilibrium condition (plus individual rationality) leave no choice for the expected payments of the different bidders.
Now, if Myerson had only proved the revenue-equivalence theorem, then he’d probably still have won the Nobel prize. But he did more, in this very same article. He also determined the revenue-optimal auction.
There is! And the key is not to necessarily sell the good to the person who values it the most, as opposed to what’s done in all classical auctions! In fact, Myerson proved that, in some cases, it’s better not to sell!
I know. Once again, that’s very counter-intuitive. Here’s one way to understand this. The seller needs leverage. Otherwise, bidders would take advantage of the seller’s sell-at-all-price behaviour, and will succeed in lowering the price. To get this leverage, the seller needs to firmly tell bidders that there are prices under which he will not sell. This threshold price is what Myerson called the reserve price. Of course, it may then be that the reserve price exceeds the bidders’ actual valuations of the good. In such a case, it is essential that the seller commits to not selling the good — incentive-compatibility relies on it! Thereby, he might lose an opportunity once in a while, but, crucially, in the long run, he will earn more.
It depends on the seller’s belief of the bidders’ valuations. Very roughly, if the seller believes that bidders have high valuations, he should set a high reserve price accordingly.
Exactly! So keep that in mind the next time you’ll get offended by local sellers’s poor treatments of you as a tourist. They’re not being xenophobe; they’re just being smart!
In the case where all bidders look the same to you, yes. But in the case where some bidders look more willing to pay than others, Myerson proved that you should use the threat of selling to other bidders to convince high bidders to bid their true valuations of the good. And this means that you should commit yourself to not necessarily sell the good to the bidder who values it the most!
It’s an interesting point. Indeed, Myerson’s optimal auction is not anonymous, in the sense that not all bidders are treated in the same way. In fact, any careful study of Bayesian theory would tell us that this is quite often the case: Optimal decisions discriminate based on beliefs (or, as some people like to call them, on prejudices). In Myerson’s auction case though, it might make you feel better that it advantages bidders who seem less willing to pay a lot for a good, who are likely to be poorer than the others…
Don’t you remember? Myerson’s revenue-equivalence theorem says that it doesn’t matter! Any auction that allocates the good exactly as Myerson’s optimal auction does will win the seller the same amount of money (in the long run).
Let’s Conclude
Unfortunately, Myerson’s optimal auction has two clear limits. First, he assumes that bidders are risk-averse. In particular, they only care about the expected gains. But, by talking to people on the streets, Derek Müller found out that this was clearly not the case, as we can see it in this Veritasium video:
But, more importantly, it only deals with single-good auction. That’s very restrictive, and, naturally, economists and mathematicians all wanted to build upon Myerson’s work to address the multi-item auction case. Well, guess what: For over three decades, no one would manage to succeed! Up until a month ago, I thought that it was hopeless. I didn’t even dare to try.
But to my great surprise, Yang Cai and his co-authors proved me wrong! In a series of three 2012-2013 papers (75 pages!), using powerful technics from computer science, they solved in the largest possible sense the auction design problem! I got terribly excited when I read their proof… And that’s what I’ll discuss in a future article! Stay tuned (for instance by subscribing!).










Leave a Reply