Happy new year to all! 2015 is the International Year of Light, and I’m starting the year accordingly (but involuntarily, I must say…)! So, you’ve probably learned about primary colours back when you were at primary school. Don’t you remember?
Yes. Exactly! But what makes these primary?
Yes. Your school teacher probably said that we can produce any colour by adding up primary colours. But why can’t we use three other colours, say brown, orange and indigo? Why are there three primary colours? Why not two or fifteen? And most importantly, what does it really mean to be adding colours? If he’s a good teacher, your school teacher probably also told you never to add apples and bananas. And here, he’s telling you to add colours. Why?
I hope you’re well seated, because we’re about to embark on a wonderful journey through the mysteries of colour additions. And this journey will take place in high dimensional spaces — spaces of infinite dimensions!
Wavelengths
To understand what primary colours are, we should start by wondering what colours are. And I can’t help recalling Newton’s (literally) brilliant prism experiment!
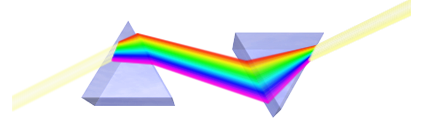
Back then it was known that using a prism, a white sunlight beam could be decomposed into the different colours of the rainbow. It was thus believed that the white light was purer in some sense, and that all other colours were byproducts of this white light. Well…
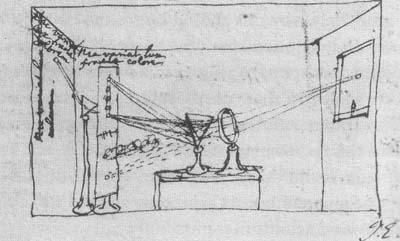
Yes indeed! And the man who proved that wrong was Newton, as he devised a simple but clever experiment.
Newton simply add a second prism behind the first one. This allowed him to recombine the lights of different colours. Amazingly, the combination of the different colours produced a white light as pure as the initial entering sunlight.
Don’t you see? It means that white light is somehow the addition of different colours.
I did. So let’s now think about what it means to add colours. For our purpose, it’s useful to think of light as a collection of individual elementary grains, called photons. Each photon has some energy, which is characterized by its wavelength. The greater the wavelength the smaller the energy.
Sort of, but not really. When all photons of a light beam have the same wavelength, we talk about a monochromatic light. Any such monochromatic light has indeed a definite colour. This is what we observe using a prism or in a rainbow.
Yes. But the converse is not true. Some colours are not wavelengths. For instance, there is no wavelength corresponding to pink. Pink can only be thought of as a combination of different wavelengths. In fact, the screen of the device you’re using to read this article is filled with colours that are combinations of different wavelengths. It it is the combination of different wavelengths that make up the colours. For instance, if you see a yellow figure on your screen, then what you’re really seeing as actually a clever combination of red and green wavelengths, and it is this combination that is indistinguishable from the yellow wavelength. This is what’s beautifully explained below by VSauce:
Now, white light is roughly made of all wavelengths between 400 nanometers and 800 nanometers. This means that, in white light, you can find photons of all kinds of wavelengths in this range — in fact, you might find even more wavelengths like infrared or ultraviolet, but our eyes do not perceive those. We can represent this variety of wavelengths by the following diagram, called the white light spectrum:
For each visible wavelength, this spectrum roughly counts the number of photons you can find in white light. The greater the peak for a wavelength, the more photons of this wavelength you’ll find in white light.
Addition
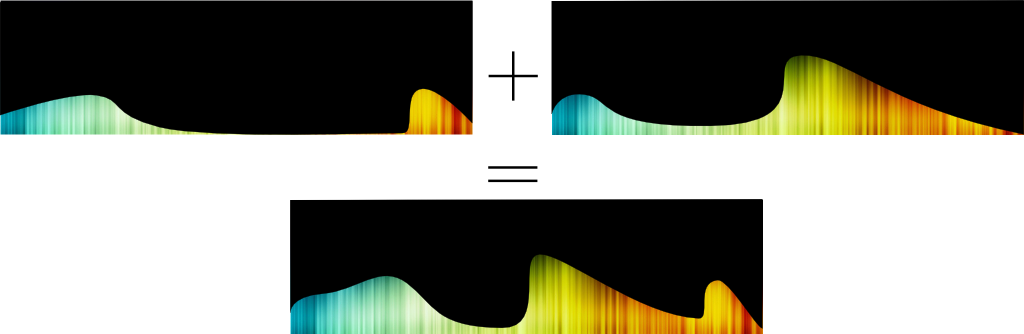
Finally, I can tell you what light addition is. It’s pretty straightforward, really. If two beams of light get merged, then the number of photons we now have is the sum of the number of photons in each beam. But, crucially, we must make sure we’re not adding things that cannot be added: We can only add up photons of the same wavelength, as photons with different wavelengths are too different to be added — like apples and bananas.
Imagine a first light beam had 1 photon of a wavelength of 500 nanometers, 2 of 600 and 3 of 700, while a second light beam had 9 photons of 500 nanometers, 0 of 600 and 100 of 700. Then, the combination of these lights would evidently be made of 10 photons of 500 nanometers, 2 of 600 and 103 of 700. All we have to do to add two beams of lights is thus to make an addition of photons for each existing wavelength.
Great, because we’re now going to take it to the next level. As I said, white light, like most light, is made of photons of a very wide range of wavelengths. Thus, we have to add plenty of numbers of photons of plenty of different wavelengths. Here’s a way to represent such an addition:
Well, it’s a new kind of addition. Here we’re not adding numbers, but the numbers of photons of each kind of wavelengths. You might call that a superaddition.
It really is! We have just invented a new natural and powerful kind of mathematical operation! This is the kind of things that really, really excite me!
OK, granted, this operation has been known for a while by now. In fact, such superadditions have become so central to modern physics, modern mathematics and modern science in general (even economics, biology and social sciences) that we now simply call them additions. But to distinguish them from the classical addition of numbers, we rather talk about the addition of vectors.
I know…
Vector Spaces
In class like in History, vectors first came up in mechanics, and, in particular, in Newton’s laws — yes, him again!
All vectors in (classical) mechanics represent some sort of coordinate. For instance, the position of an object in a referential is given by three coordinates. One coordinate gives the up-down location, another gives the left-right location and a third one gives the front-back location. Crucially, one’s position is perfectly defined once and only once you know all three coordinates.
Exactly! But there’s more. We can add locations or subtract them — subtraction is in the end just a variant of addition. For instance, we can subtract the coordinates of a car at a certain time from its coordinates one hour later. This subtraction will give the variation of the car’s location within one hour: This measures the average velocity of the car!
Similarly, the addition of forces you apply to an object is an addition of vectors. Indeed, forces have different coordinates, and the addition of forces boils down to the additions of the coordinates of the forces. This is what’s explained in the following SixtySymbols video:
Well…
Dimensions
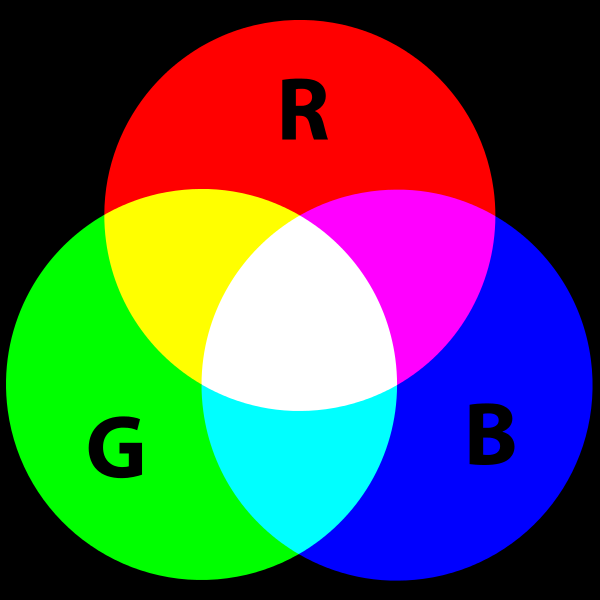
There’s also that magical number 3. Remember? There were 3 primary colours…
This is because our eyes are not that sophisticated. As VSauce explained it, our eyes only have 3 different kinds of receptors, called cones. Roughly, one captures blue, another captures green, and the third one captures red. And that’s why there are exactly 3 primary colours, and that those colours are blue, green and red!
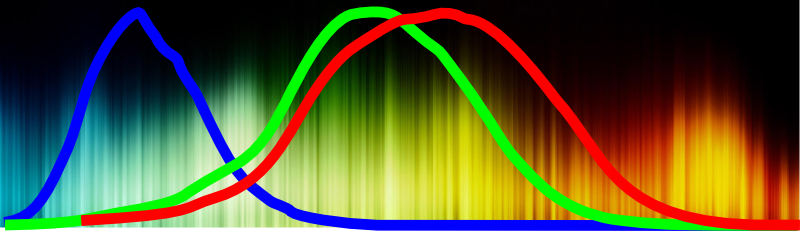
Actually, it’s a very rough simplification to say that the red cone see the red colour. It actually sees a wide range of colours that are more yellow-greenish than red. More precisely, the following figure shows what colours the different cones capture.
As you can see, the green and red cones actually absorb more or less of the same wavelengths. For instance, they both absorb the yellow wavelength, although, the green cone absorbs slightly more of it than the red cone does — this means that there are slightly more yellow photon that the red cone fails to detect.
Well, roughly, what cones do is that they count the number of photons they absorb. Then, each cone tells the brain how many photons it has absorbed. In the end, for a point he’s staring at, the brain receives a triplet of numbers of photons received by the three different receptors. For instance, if the eye looks at a monochromatic yellow light, it will see the green and red cones will catch many yellow photons, but the red cones will catch more of them. Thus, we would see 0 by the blue cone, 54 by the green cone and 87 by the red cone. We may represent the light this corresponds to by the triplet (0, 54, 87). Do you see the relation with vectors of mechanics?
Exactly! Now, in principle, a perfectly red colour would be one that only gets observed by the red cone. It should yield a triplet like (0, 0, 100). Importantly, this requires other cones not to detect any photon. Look at the figure above. The only case where this can happen is for a red monochromatic light. This is why we say that the red cone is the red cone: It is not because the red cone absorbs the red light; it is because a light that is red only gets absorbed by the red cones only.
It is. Similarly, the perfect blue is something like (100, 0, 0), and the perfect green something like (0, 100, 0). But you might notice that there is no such a thing a perfect green: Whenever the green cone absorbes something, either the blue or the red cone absorbes something too. But this is a small detail. For simplicity, let’s assume that there is such a thing as the perfect green. Importantly, blue, green and red are primary colours, because any triplet our brain sees is a triplet that can be produced by a combination of blue, green and red. For instance, the triplet (24, 64, 32) is also a combination of a perfect blue (24, 0, 0), a perfect green (0, 64, 0) and a perfect red (0, 0, 32).
Exactly! All we see are triplets. But importantly, this is merely because we have three different cones of light. Some of us are more or less color blinds. One possible cause is the malfunction of one or several kinds of cone, which restricts the vision of colours to a tuple of two values or less.
It is! Some birds have 5 or more different cones, which allow them to see many more different colours. In mathematical terms, the colours they see live in spaces of 5 dimensions or more! How cool is that?
As VSauce explained it, there are beams of light with different wavelengths that are seen by our eyes as the same colours. That’s the case of a light with only the yellow wavelength and a light with both red and green wavelengths. To our eyes, both correspond to a triplet like (0, 54, 87). We cannot distinguish these. But a bird can. For a bird, the yellow-wavelength light and the red-and-green-wavelengths light are different colours.
Definitely. In fact, in principle, the perfect eye would see light as it really is: It would the spectrum of light. It’d be able to count how many photons of any frequency he sees. Such an eye would have a vision of (nearly) infinite dimension, as there are (nearly) infinitely many frequencies light can have.
It’s not that crazy! To do so, all you need is a prism, and infinitely many (or at least, sufficiently many) captors for each diffracted wavelength.
Linear Algebra
Okay, I might have been exaggerating about claiming that light lives in an infinite dimension space. After all, I told you that light was made of photons, and there are finitely many photons. So, the spectrum of a beam of light might rather be of finite dimension. Still, its dimension is definitely huge, probably around $10^{50}$. In any case, you see that the use of very high dimension spaces is of essential use to merely model something as simple as light.
That’s exactly what I’m suggesting. In practice, real-life systems are similarly of very high dimensions. What is the best policy against unemployment? This question depends on so many diverse factors (for instance, current GDPs, shares of new technology, security deployment, external competition…) that it is in essence a question about very high dimension spaces. In fact, the mere measurement of unemployment can only be rigorously done in a very high dimension space. After all, what is really meant by unemployment? Are partial-time jobs unemployment? Are jobs in the black market unemployment? Are entrepreneur unemployed? The best answers to these questions aren’t yes-or-no answers. They lie in making several measurements and giving answers in very high dimension spaces: 15% of people have partial-time jobs, the economics of black market is 5% of GDP, 1% of people are entrepreneurs… In fact, as you’ve guessed by now, very high dimension spaces is just the mathematical terminology for Big Data!
Yes! That’s why it has become essential for our understanding of real-life systems to get a good feel for very high dimension spaces. This is the art of linear algebra. Roughly, it is very difficult to navigate within very high dimension space, unless there is some sort of linear structure.
A very high dimension space with a linear structure is a space where we can combine data of this space using some sort of superaddition. Once again, I’m being a bit mystic: We in fact simply talk about vector addition. If we can add elements of a space, we talk about a vector space. Vector spaces have become a central figure of all of science, and their star feature — at least, outside of pure maths — is the matrix.
The movie assumes that the world is the matrix… which, if the world is indeed finite, kind of makes sense to me! Anyways, to be less mystic once again, a matrix is just an array of numbers. In other words, it is a structured way to represent plenty of coordinates. And that’s super useful! A lot of computers basically just manipulates matrices to perform more powerful computations. This is what’s beautifully explained by Bill Shillito in this great TedEd video:
Matrices can be thought of as operations that transform some vectors into other vectors.
Let me give you an example. As we’ve seen, the spectrum of a light beam is a vector of very high dimension. That’s not what we see. As we’ve said, the brains only see a triplet — that is, a 3D vector. So, really, what the cones of our eyes do is really to transform the very high-dimensional spectrum of a light beam into a 3D vector. This transformation is exactly a matrix.
Well it’s a very high dimensional matrix! Indeed, the number of its columns is the dimension of the spectrum of the light! But here’s a rough way to represent it.
Each row represent a cone colour, each column a light wavelength, and each entry is, on a scale from 0 to 9, how often a cone manages to catch a photon of a given wavelength. Amazingly, if $X$ is the vector corresponding to the spectrum of a light and $M$ is the matrix above, the matrix product $MX$ is exactly the triplet observed by our brain!
Let’s Conclude
I had already written about colours. But that was a long time ago, and I think I might have improved my writing… More importantly, I got the idea of working the theory of linear algebra from the basic concepts of colours. Hopefully, this has shed some (literally) new light on the abstract concepts of vectors and matrices, in pretty cool way! And if you really enjoyed this, you’ll probably enjoy the Youtube video I made on this topic:
Now, the story of this article is far, far from being complete. As we have said, ignoring light brightness, we may say that triplets like (0, 10, 20) and (0, 5, 10) have the same colour. This means that instead of colours ranging in a 3D space, they rather range in a 2D space. Moreover, the primary colours are not actually primary. This is mainly because there is no perfect green light. Thus, whenever the green cone catches photons, so does either the red cone or the blue cone. As a result, many greenish wavelengths cannot be reproduced using the green of the primary colours. This is roughly what’s explained by Henry…
He also argues that violet is not part of the spectrum, and explains why we tend to see it in rainbows anyways, in this video.


Leave a Reply