In schools, we’ve all learned Newton’s laws as some blatant fact about our universe. I too made a video that celebrates them and presents them as an obvious truth.
Yet, have you ever really meditated them to the point where they feel stupidly wrong? After all, they’ve only been discovered some 350 years ago, which means that it had totally escaped millenia of human thoughts. In fact, I’d bet that most Ancient scholars would harshly discredit them on the ground of their obvious absurdity. I suggest you deeply ponder them for a few minutes…
Hummm… You know what? Let’s just listen to Derek Müller on Veritasium instead. His fantastic video below points out the misconceptions of our intuitions.
They are. Derek’s laws are both very intuitive and fundamentally incorrect. Conversely, Newton’s laws are both very counter-intuitive and much more correct.
He did. But Newton’s laws are still amazingly fit to describe virtually all mechanical motions we are familiar with, from the falling of an apple to the orbits of the planets of the Solar system. From our daily lives to rocket science, at our macroscopic scale and in our time scale, Newton’s laws are so extremely accurate that it’d be pointless to replace them by Einstein’s relativity. Indeed, the predictions of the two theories would coincide nearly perfectly.
Yes. And yet, as Derek just showed you, they are already unbelievably counter-intuitive. Let’s review them in details!
The First Law – Inertia
Intuitively, all objects in motion will exhaust and slow down. After all, it takes energy to get in motion, whether this energy is the burning of calories or the that of fuel. And when this energy dries out, obviously, the object cannot move anymore. There are so many examples of that! Kick a ball, drive a car or look at Usain Bolt. Every unperturbed object in motion seems doomed to end up still. It sounds clearly true, right?
The answer is literally in the sky.
On earth, there’ll always be something to perturb the motion of an object. The ball may be stopped by a net, the car may crash on a wall, and Usain Bolt may use frictions with air and the ground to slow down. However, up there, through the void of the cosmos, little can perturb the motions of astronomical objects. And thus, if we really want to understand the nature of unperturbed motions, it’s only by looking up there that we can find an answer. This is what Galileo did and, more importantly, this is what Newton did. They found out that, up there, moving objects do not seem to slow down.
That’s right! This is precisely Newton’s first law, which is sometimes referred to as the law of inertia. It says that, if unperturbed, objects will carry on their motions eternally. They do not speed up, and more counter-intuitively, they do not slow down. A beautiful example of that is our rotating Earth. It used to rotate. Thus, by Newton’s first law, it will eternally rotate, as demonstrated by Derek in this other video:
What’s very troubling with Newton’s first law is that it never applies! Crucially, in real life, no object is unperturbed. Even astronomical objects up there are under gravitational influences. This is why this first law is so counter-intuitive. It is an abstract principle that makes the whole theory consistent. Yet, it never applies to reality. When you ponder this, it’s even hard to imagine that the law of inertia is regarded as the first and most basic law of all physics! After all, it’s hardly testable!
Technically, Newton’s first law is pretty useless, as it can be regarded as a mere particular case of the second law! Nevertheless, it is an interesting first step to dive into Newton’s picture the world. And it unveils in quite an obvious way just how counter-intuitive the laws are. In fact, the effort to make sense of it is pretty enlightening.
Imagine you were served coffee on a plane. Coffee falls downwards, yet the plane is flying at high speed horizontally. Do you think that the air hostess would aim ahead of the cup to pour coffee? Would she pour it like on the left of the figure below, or like on the right?
Galileo did himself this thought experiment (with a ship instead of a plane). Amazingly, he concluded that, if the motion of the plane was constant, then the left solution was the right one. More generally, the laws of physics should not be modified within a system in constant motion. The physics in the plane shall be exactly the same as the physics on Earth. This idea is known as the principle of relativity. And this mere principle of relativity suffices to derive Newton’s first law.
The key is to remark that motion is relative. The coffee cup is still with respect to the air hostess. And yet, it is moving at very high speed with respect to the peasant looking up at the plane from his fields. Amazingly, the obvious fact that, if unperturbed, the coffee cup will indefinitely remains still with respect to the air hostess also implies that it will keep its very high speed with respect to the peasant. That’s why, from the peasant perspective, unperturbed objects will preserve their motions indefinitely.
The Second Law – Dynamics
The most fundamental law of Newton’s laws is the second law. It is by far the weirdest of all. That’s partly because it involves three concepts which are all trickier than they sound.
First is the concept of force. What do you think that is?
Hummm… The trouble is that the word power means something else in physics. Power corresponds to the amount of energy we transfer to the object, or that the object transfers to us. Let’s take the example of a goalkeeper catching ball. By applying a force on the ball, the goalkeeper is actually retrieving kinetic energy from the ball. So, weirdly enough, in many cases, applying a force may correspond to the opposite of giving power to an object! Similarly, when you’re holding a heavy rock in your hands, you are applying a big force to the rock to keep it from falling. Yet, you’re transferring no energy to it! So, weirdly enough, a strong force may have no power.
The Wikipedia definition says that it’s what influences the motion of objects… but this boils down to saying that force is defined by Newton’s second law! That’s not what we want, as it’s supposed to be used to define Newton’s second law. In other words, Wikipedia definitions yield a troubling circular definition of forces and Newton’s second laws. That’s how weird and counter-intuitive the mere concept of force is!
A good definition is given by Derek in the next video:
So, according to Derek, a force is a push or a pull. This push or pull is characterized by a direction and a value. For instance, the gravity force of a planet pulls an object towards the center of the planet with a value proportional to the mass of the planet, propotional to the mass of the object and inversely proportional to the square of the distance between the planet and the object centers of mass.
This is what Newton must have thought. So he reused René Descartes’ algebraic geometry to sum up all the information about a force into a single mathematical object called vector. This vector has two representations. One is geometrical: A force is an arrow determined by a direction and a length. The other is algebraic: A force is a collection of 3 values of the force. Each value stands for the strength of the force in one of the 3 spatial directions. Accordingly to Descartes’ dictionary, there’s a natural translation between these two representations of vectors. Namely, the three algebraic values of a force are the coordinates of the geometric arrow. Here’s an example in dimension 2.
The second concept is called inertial mass, also known as inertia or mass. Once again, our intuition is usually very wrong about what this inertia is. And, once again, this misconception is beautifully unveiled by Derek:
Following Derek’s words, inertia is not to be confused with weight. While weight is the downward force caused by gravity, inertia, in Wikipedia’s words, is the resistance of an object to change their motion. However, once again, this definition is flawed as it leads to a circular definition between inertia and Newton’s second law…
The trouble with the idea of mass, is that it’s both related to inertia and weight. And yet, a priori, there’s no reason why heavy objects should have greater inertias! This is why physicists have long distinguished inertial mass from gravitational mass. The former is the one we’re interested in right now, while the latter is the one that intervenes in the law of gravity.
Once again, I’ll just steal Derek’s words. Inertial mass is just a measure of the amount of matter in an object.
This one is by far the worst. It is acceleration, and I strongly suspect it to be the source of most students’ mistakes.Here’s another Derek’s classic to keep that in mind:
As it turns out, the right answer is d, where, according to Derek, the acceleration is twice that of a. It’s very counter-intuitive because we tend to confuse acceleration and speed. Importantly, acceleration is not speed nor velocity. An object may have a strong acceleration while barely moving at all.
It’s the direction and value at which motion changes. At the bottom of the jump, the motion of the jumper completely changes. He was going down quickly, and next thing he knows, he’s going up quickly too. By opposition, at his maximal speed, the jumper’s motion doesn’t change at all. He just keeps going down at the same maximal speed.
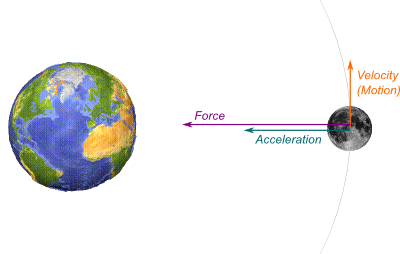
No. Acceleration is not the change in speed. It is the change in motion. Take the example of the Moon. The Moon is constantly accelerating towards the Earth. And yet, its speed remains constant. But, crucially, its motion doesn’t. At any time, its motion gets curved towards the Earth, because it accelerates towards the Earth.
Exactly. That’s why, just like forces, accelerations are vectors. An acceleration is thus geometrically represented by an arrow, and analytically by three coordinates.
Better than that. Newton’s second law asserts that the forces on an object are what determine its acceleration. In other words, the acceleration of an object is an arrow which has the same direction as the sum of the forces acting upon it. So, for instance, the Moon accelerates towards the Earth, because the force of gravity pulls it towards the Earth.
Yes. More precisely, the value of the acceleration is proportional to the strength of the forces. The greater the force you apply to an object, the more you modify its motion. The value of acceleration is also inversely proportional to the inertial mass of the object. This means that the more stuffs there is, the harder it is to affect its motion. We can sum up this second law with an elegant and simple four symbol mathematical formula:
At first glance, this formula should look like a mermaid driving us away from Truth because of its misleading elegancy. How could physics be reduced to such a simple equation? Plus, why is acceleration involved? Is it not the motion that we affect, rather than the change in motion? Our intuitions say that if we want to get up, then we can get up. If we want to get going, then we get going. In other words, our intuitions say that we control our motion and the motions of the objects around us. And in most video games, that’s what we do. We control the motions of our heroes.
Crucially, according to Newton’s second law, the answer is no. Our intuitions are fundamentally mistaken. We cannot control motions directly. At best, we control the changes in motions! To fully grasp, seize and feel Newton’s second law, I suggest you ponder that sentence longly.
I don’t know! But it’s been tested over and over, and has given so many right predictions. This law is still the one we use to send rockets in orbits or to design powerful mechanical machines. It is accepted by all, because careful experiments have shown that it was trustworthy. However unlikely that may sound.
The Third Law – Action / Reaction
The third law is the one everyone knows. After all, it has a very nice phrasing: For every action, there is an equal and opposite reaction. I suspect many to have reused this phrase with a totally different meaning to Newton’s. Somehow, on a philosophical level, it sounds a lot like karma. And I guess that’s why we’re fine with it when we first hear it. Yet…
Yet, it’s just as stupid as Newton’s other laws! Why on Earth would there be this equal and opposite reaction? My father has scolded me times and times but I hardly ever got to scold back at him. On a more physics level, the Earth is pulling me with an enormous force. Yet, it sounds completely dumb to say that I am pulling the Earth with an equal force…
Check Derek’s interviewees on a similar physics example:
So, as it turns, you are pulling the Earth just as much the Earth is pulling you.
You do a little bit. But the Earth has such a huge inertial mass that, to make it accelerate, it takes a much much bigger force than the force it exerts on you. Keep that in mind. Big forces applied to enormous inertial masses induce little accelerations, as asserted by the second law.
Let’s see one essential application of this third law which will help us understand it: Rocket science. Well, actually, let’s see Derek explain rocket science to us!
Derek’s explanation of rocket science lies in the the third law. While the rocket pushes away its propellant, by the third law, the propellant pushes back the rocket with an equal and opposite force.
It’s not. Intuitively, I guess that most people would say that the force of the rocket on its propellant is much greater than the force of the propellant on the rocket.
As I said, the third law can be derived from the additivity of the second law. Consider the rocket and its propellant as a whole system. Assume that there is no external force acting on them, as they are traveling in outer space. Then, by the first law, the system as a whole should maintain its motion indefinitely.
Now, if we look at the details of all forces, then the total force on the system must also include internal forces. Namely, we should include the force of the rocket on the propellant and the force of the propellant on the rocket. But since the system as whole maintains its motion indefinitely, this also means that the sum of all forces is zero. Hence, the force of the rocket on the propellant and the force of the propellant on the rocket must add up to zero. In other words, each one is necessarily equal and opposite to the other!
Let’s Conclude
In conclusion, I should say that there actually is only one law: The second law. In total generality, this second law asserts that for any collection of matter, the sum of all external forces acting on it divided by its total inertial mass must equal the acceleration of its center of mass. From this law, all other laws can be derived! When you think about it, it’s completely astonishing that this single law governs nearly perfectly most of the physics we know. In this powerful, predictive and elegant law lies the beauty and conclusiveness of Newton’s laws. Even though these are highly counter-intuitive.
I do think so. Check this last video of Derek’s about his PhD to see why:
Here’s one last exercise for you. Below is a wonderful TedEd video by Joshua Manley on Newton’s laws. It is beautifully illustrated, very well explained and definitely accurate. Yet, I want you to imagine what misconceptions a half-listening and untrained audience could have kept (or obtained!) after having watched it:




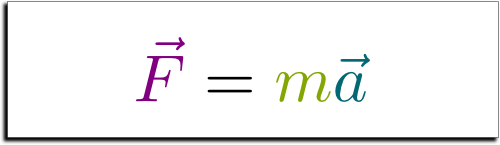

Leave a Reply