Intro
Crisis. Most analysts believe that it’s a financial crisis. Others say it’s a crisis of the economic system in general. Others speak of political crisis.
I’ll tell you what its real cause is: it’s a crisis of egoism. And I’m going to prove it in a mathematical way. We’ll show it through a football (soccer if you prefer) example. And we’ll consider the context of the 2012 European Championship for national football teams organized by UEFA, hosted by Poland and Ukraine.
The dilemma
The competition system for the final tournament is based on two rounds. In the first round, the 16 teams are divided into 4 groups of 4 teams. In each group, teams play a round-Robin, which means they all face every other group’s teams. The winner and the runner-up of each group are determined by the numbers of points the teams have won (3 points for a win, one point for a draw, no points for a defeat).
If two or more teams are equal on points after completion of the group matches, then the ranking is defined by the following criteria are applied, in the order given:
- higher number of points obtained in the matches among the teams in question
- superior goal difference in the matches among the teams in question
- higher number of goals scored in the matches among the teams in question
- superior goal difference in all the group matches
- and finally, a lot among the teams (let us modify the last real rules, in order to establish an equiprobability among the teams).
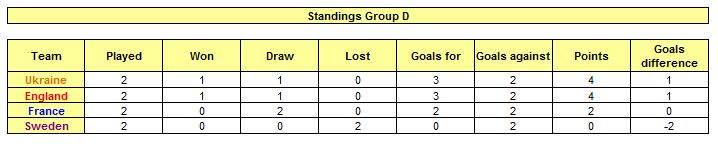
The previous days’ results in Group C are as follows:
Ukraine 2 – Sweden 1 France 1 – England 1
Sweden 1 – England 2 Ukraine 1 – France 1
Today, the national teams from Sweden and France and the teams from Ukraine and England are playing the last matches of Group D, which have been kicked off at the same time. After these matches, the first two teams of the group qualify for the next round.
There are 2 minutes left before the end of the two matches. In the first one, the current result is France 1 – Sweden 0. Both coaches have already made all of the allowed player substitutions, and the match is much disputed, so that there is equally likely to score any of the two teams. Thus, we assume for our purposes that three results may occur, all equally likely: France 2 – Sweden 0 (if France scores), France 1 – Sweden 1 (if Sweden does) and France 1 – Sweden 0 (if none of them scores a goal).
Now we will focus on the other game, between England and Ukraine. 2 minutes before the end, the score is tied at 1. Both coaches have already made two player substitutions, and are preparing their third and last one. They may make an attacker change (remove a defender and add a striker) or a defensive one (remove a striker and put a defender).
The two coaches from England and Ukraine will make their substitutions simultaneously, and none of them knows what will be the opponent’s move.
- If both coaches choose an attacker change, any of the teams can score a goal, and the other one will not have time to draw the match.
- If one coach makes an offensive change, and the other one makes a defensive one, only the team with an attacker strategy will have options of scoring a goal.
- And if both coaches make defensive changes, the match will necessarily end in a draw.
The question at this moment of the game is…
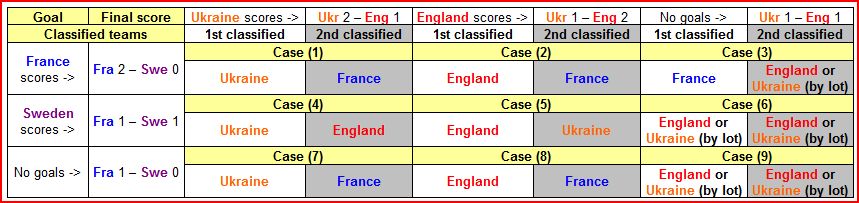
Let’s look at the table with the different scenarios that can occur, and the different consequences of the decisions taken by the coaches on the probabilities of qualifying.
We can see that when both coaches have to make a decision on their strategy, we get 4 different situations, depending on whether they make an attacker or a defensive change: Ukraine and England go to the attack, Ukraine attacks and England defends, Ukraine defends and England attacks, or both teams choose defending.
Let’s do England’s coach’s reasoning (the conclusions for Ukraine’s coach are the same).
a) England’s change is offensive, and so is Ukraine
If England’s change is offensive, and so is Ukraine, there are 9 possible cases that can occur with equiprobability (either England or Ukraine can score a goal or not, but remember there’s no time to score 2 goals):
(1) + (2) + (3) + (4) + (5) + (6) + (7) + (8) + (9)
In 6.5 of these cases England would pass the next round:
(2) + 50% (3) + (4) + (5) + (6) + (8) + (9)
b) Your England’s change is offensive, but Ukraine’s isn’t
If you make an offensive change, but Ukraine prefers defending, England may score a goal or not, but sure that Ukraine will not, so now we have 6 possible cases:
(2) + (3) + (5) + (6) + (8) + (9)
(2) + 50% (3) + (5) + (6) + (8) + (9)
Now we’ve got a 5.5 / 6 = 91.67% probability of qualifying.
a/b) So if England decides to go on the attack, the expected probability of qualifying will result in an average probability of the two possible cases, also equally likely, ie that Ukraine goes on the offensive or prefers defending, and therefore we will have a chance of (72 , 22% +91.67%) / 2 = 81.95% of qualifying.
c) England’s change is defensive, and Ukraine’s is offensive
In this case, we know that England won’t score any goal, but there is a 50% chance that Ukraine scores. Thus, we have 6 possible cases:
(1) + (3) + (4) + (6) + (7) + (9)
50% (3 ) + (4) + (6) + (9)
So we’ve got a 3.5 / 6 = 58.33% probability of qualifying.
d)England’s change is defensive, and so is Ukraine’s
In this case, the outcome of the match is a draw, as none of the teams will have an option of scoring a goal. Now we have only three possible cases:
(3) + (6) + (9)
50% (3) + (6) + (9)
c/d) We summarize now what happens if England opts for a defensive strategy: the expected probability of qualifying will result in an average probability of the two possible cases, also equally likely, ie that Ukraine go on the offensive, or prefers defending, and so we will have a chance of (58.33% +83.33%) / 2 = 70.83% of qualifying.
If we compare the two possible strategies, a/b) or c/d), the one which provides a greater chance to qualify is going to the attack (option a/b). And no matter what Ukraine does, England’s better option is always to attack. Therefore, the English coach surely will make an attacker change. And as we said that the situation was exactly the same for Ukraine, his coach, following the same criteria, will also make an attacker change.
Hence, as we can see, each team will have a 72.22% chance of qualifying.
However, and this is where the paradox occurs, this is not the most favorable option for both teams. If both coaches agreed on their changes, sharing information among them, both would have concluded that it was better to make a defensive change, since in that case the chances of each team of qualifying would be of 83.33%, much better than with the elected strategy, which provides a 72.22% probability!
The original prisoner’s dilemma
Surely many of you have recognized in this story the famous prisoner’s dilemma.
This dilemma consists on a game analyzed in game theory that shows why two people might not cooperate, even if it seems that it is in their best interest to do so. It was originally devised and discussed by Merrill Flood and Melvin Dresher, both working at RAND Corporation in 1950 where they were looking for possible applications to global nuclear strategy. Some years later, Albert W. Tucker (a Princeton mathematician) formalized the game with prison sentence payoffs and gave it the “prisoner’s dilemma” name, making Flood and Dresher’s ideas more accessible to most people. Soon, the dilemma attracted widespread attention in a variety of disciplines so that now this dilemma is the best-known game of strategy in social science and, for some authors, is considered the most influential one in the social sciences (economics, politics, sociology) in the latter fifty years.
This problem is presented as follows:
Two burglars are arrested under the suspicion of having committed a crime together, but the police do not have enough information in order to have them convicted, so they are isolated from each other by the police, and are offered a similar deal:
- If one burglar defects/betrays/testifies against his partner, and the other burglar does not confess, the betrayer will go free, while the other burglar will go to prison for 20 years on the maximum charge.
- If each confesses and implicates the other, both will go to prison for 10 years.
- If none of them confesses and remain silent, then both will be sentenced to one year in jail for a minor charge because of lack of proof.
Each has to choose whether or not to confess and implicate the other (either ‘cooperate’ or ‘defect’). What should they do?
We can express the strategies in a “payoff table”:

If it’s supposed that each player is only concerned with lessening his time in jail, the game becomes a non-zero sum game. And its symmetry leads each burglar to betray the other, even though their individual ‘prize’ would be greater if they cooperated. This means that an individually rational action leads to worse results for each person.
This dilemma has other studied versions, just modifying the number of burglars, changing the symmetry of the payoffs, playing it over and over (in this case, at the end, the two prisoners will also choose betraying each other repeatedly), and further more.
As you can imagine, the prisoner’s dilemma is a matter of interest for economics, politics, sociology, and other social sciences, as it states that often when each person pursues his private interest, does not promote the collective interest of a group.
The conclusion
Now and finally, you can translate this example to the real world. In most situations people could gain important benefits from sharing information and cooperating. But that’s not the common way of doing things in our actual world.
This is one example of how mathematicians may help on the solution of crisis. If you have reached the final of this article and you have learned this mathematical dilemma, surely you’ve got an advantage over many people. I hope you put it in practice. You’ll get excellent results from the beginning!
Just remember: share information, cooperate, and don’t be egoistical. Ah, and a bit of Maths! This may be the best way of changing the world into one better one.