I had just finished reading his book La Science à l’usage des non-scientifiques when, sadly, Albert Jacquard, aged 2.06, passed away, on September 11, 2013.
That’s how he liked his age to be given! And, to pay tribute to this renowned geneticist and great science popularizer, I’ve decided to write this article to explain how and why he liked ages to be given that way!
Logarithms and Scales
Before getting to age counting, let me first introduce logarithms, which are the key mathematical objects to describe ages as Albert Jacquart liked to do it.
The logarithm is an operator to solve equations like $10^x = 100$.
Yes! That’s why we write $\log_{10} (100) = 2$.
Mathematicians like to study the solutions of equations… But more practically, the logarithm is an amazing tool to write down in a readable way extremely huge or extremely small number. For instance, the logarithms of all the scales of the universe only range between -35 and 27! This is what’s remarkable with logarithms! They enable to capture all the scales of the complex universe with two-digit numbers! These scales are obtained with logarithms are called logarithmic scales. For an awesome example, check this awesome animation by Cary Huang on htwins.net.
Yes! But that’s not all. In fact, that’s not where they are used the most! Many other measurements are made with such logarithm scales. This is the case, for instance, of decibels, used to measure the intensity of signals, like in acoustics or photography, as you can read it in my article on high dynamic range. In both cases, sensors like our ears, eyes, microphones or cameras have the amazing ability of capturing a very large range of sound or light intensities. For instance, our eyes can see simultaneously a dark spot and a spot a million times brighter, while our ears can hear sounds from 0 to 120 decibels, the latter being 10^12 times louder than the former! Making sense of these large scales is more doable with logarithmic scales!
Another important example is the measure of acid concentration in water (the pH), as explained in this great video by Steve Kelly on TedEducation:
Yes. But let’s talk about other bases later…
One area in which logarithms are essential is to describe of growth. Because logarithms capture huge numbers with small numbers, it means that it takes an extremely huge numbers for its logarithm to be big. Mathematically, we say that logarithms have smaller growth than any function $x^\alpha$ for $\alpha > 0$. Thus, we often use them as a benchmark to discuss small growths. A crucial example of that is the fundamental prime number theorem.
The prime number theorem is a characterization of the distribution of primes. First observed by Carl Friedrich Gauss, it was later proved by Hadamard and de la Vallée-Poussin. It says that the average gap between consecutive primes grows as we consider bigger and bigger numbers, and this growth is the same as the growth of logarithms. But, rather than my explanations, listen to Marcus du Sautoy’s:
Other important examples of comparisons of growth appear in complexity theory. You can read about it, for instance, in my article on parallelization.
Age Counting
From a mathematical perspective, being able to write down huge numbers isn’t a ground-breaking achievement. That’s not what makes logarithms essential to mathematics. What does is their ability to transform multiplications into additions. And that’s the key property of logarithms which led Albert Jacquart to propose to use them to define ages.
Albert Jacquart noticed that there was not as much age difference between a 25-year old girl and a 45-year old man as there is between a 5-year old girl and a 25-year old. This idea is illustrated by the following epic extract from Friends, where Monica tells her parents that she is dating their old friend Richard:
Well that’s not that surprising when you think about it. After all, a 25-year old man has lived 5 times longer than a 5-year old girl, but there’s not such a big ratio between a 45-year old man and a 25-year old girl.
Well, sort of… According to Albert Jacquart, the reason why age difference doesn’t mean what it should mean is because we’re not using the right unit to measure age!
Our measure of time is fine. But what’s misleading is our way of saying how old we are! In particular, a right way to express age difference should rather correspond to the ratio of the amounts of time lived.
The first step is to compare lifetime to a relevant characteristic amount of time which represents life. Albert Jacquart liked to choose the human gestation duration (9 months). Then, he proposed to write the number of gestation duration we have lived as a power of 10. And this power would then be defined as the age. In other words, the age is now defined as the logarithm of the number of gestation durations one has lived. This corresponds to the following formulas:
Recall, that the Age in the formula is how Albert Jacquart defines it! It’s not what we usually call age!
25-year-old Monica has lived 300 months. That’s $300/9 = 33$ gestation durations. Thus, her age is $\log_{10}(33) \approx 1.52$. Meanwhile, 45-year-old Richard has age $\log_{10}(45 \times 12/9) \approx 1.78$.
Well, we said that what matters is the ratio of the amount of times people have been alive, right? So, to compare the ages of Richard and Monica, we would have to divide the respective Richard’s lifetime by Monica’s lifetime… And, magically, we obtain the following equation:
So the ratio of lifetimes now corresponds to… an actual age difference! That’s what we wanted!
The age difference between 25-year-old Monica and 45-year-old Richard is $1.78-1.52 \approx 0.26$. Twenty years before that, the age difference was $\log_{10}(25 \times 12/9) – \log_{10}(5 \times 12/9) = 0.70$. Compared to twenty years earlier, Monica and Richard are now nearly the same age! Plus, wait another 20 years, and their age difference would then be 0.16…
Products Become Sums
This ability logarithms have to transform multiplication into addition is the core of its potency in mathematics. Before computers were invented, this yielded a powerful way to quickly compute huge multiplications, as explained in the following video by Numberphile:
Pretty much! But that’s not the only application of the ability of logarithms to transform products into sums. In statistics, to adjust models, one classical technics consists in searching for parameters which make the observations the most likely. This is known as the maximum likelihood estimation method. It’s the one I used to estimate the levels of national football teams to simulate world cups!
The likelihood is then a probability of a great number of events occurring. Assuming these events independent, the likelihood then equals the multiplication of the probabilities of the events. Yet, to maximize the likelihood, the classical approach consists in differentiating it. And, as you’ve probably learned it, differentiating a product is quite hard. The awesomeness of logarithms is to transform the product into a sum, which is infinitely easier to differentiate!
The moral is that, whenever you must differentiate a complex product, try to differentiate its logarithm instead!
Another area where logarithms are essential is Shannon’s information theory and entropy in thermodynamics. In particular, to express the amount of information a system can contain, Shannon had the brilliant idea to consider it to be the logarithm of the number of states it can be in.
When you have two hard drives, the number of states they can be in is the product of the number of states each can be in. By using Shannon’s quantification of information, called entropy, the amount of information two hard drives can contain is now the sum of the amounts of information of each of them! That’s what we really mean when we say that 1 Gigabytes plus 1 Gigabytes equals 2 Gigabytes! Behind this simple sentence lies the omnipotence of logarithms!
From a pure mathematical viewpoint, this ability of logarithms to transform products into additions is a fundamental connection between the two operations. We say that logarithms induce an equivalence between products of positive numbers and sums of real numbers.
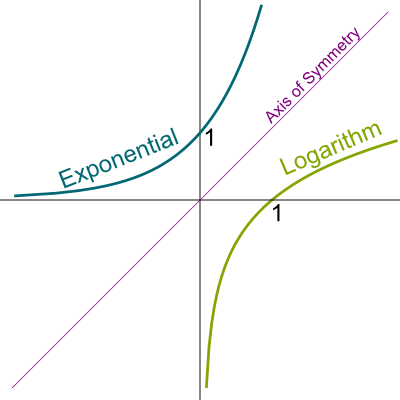
Yes! The other ways around are known as exponentials. Exponentials transform sums into products. Just like logarithms, exponentials are defined by a base. If an exponential and a logarithm are defined with the same base, then the exponential of the logarithm and the logarithm of the exponential get us back to our initial point. For instance, $\log_{10} (10^x) = 10^{\log_{10}(x)} = x$. Geometrically, this beautiful property means that the main diagonal is an axis of symmetry between the graphs of exponentials and the graphs of logarithms, as displayed in the figure on the right.
Calculus and Natural Logarithm
The area where logarithms have strived the most is calculus, especially in differential and integral calculus.
That’s because the primitive of $1/x$ is… a logarithm!
Hehe!!! Let’s prove it! Let’s show that the primitive of $1/x$ transforms multiplications into additions. Since only logarithms can do that continuously, this will prove that the primitive must be a logarithm.
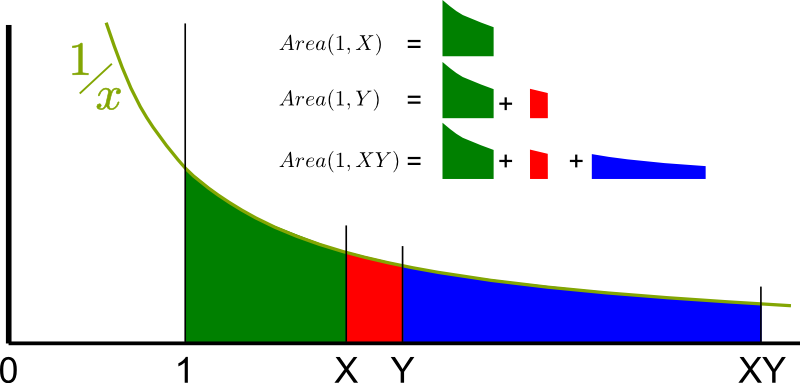
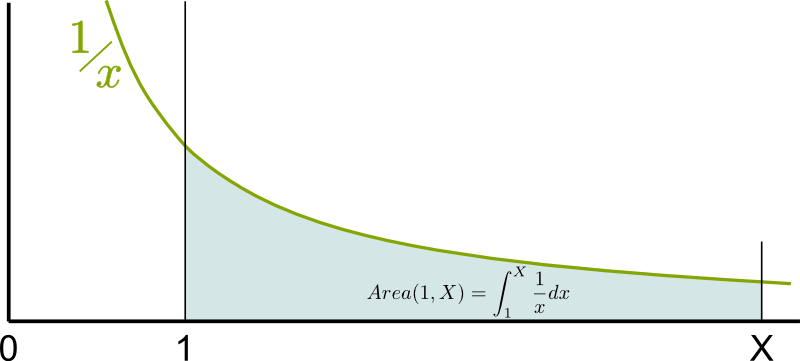
A primitive is a measure of the area below the curve. In our case, the primitive we will be focusing on equals the area below the curve $1/x$ between $1$ and $X$, as described below. Let’s call it $Area(1,X)$, instead of its usual complicated notation $\int_1^X dx/x$.
Now, I want you to prove that $Area(1,X)$ is actually a logarithm of $X$!
Come on! It’s a cool exercise!
Read what I’ve just said earlier!
Yes! What does that mean?
Exactly!
When I’m stuck, I like to doodle…
Here, let me help you out:
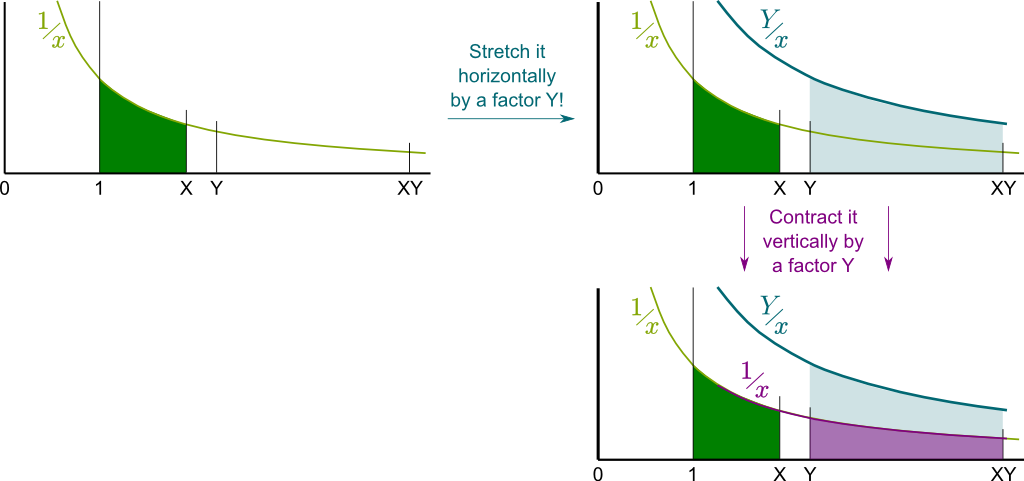
So, to prove $Area(1,X \times Y) = Area(1,X) + Area(1,Y)$, what you really need to prove is that…
Exactly! Technically, what you’ve just used is Chasles relation $Area(1, X \times Y) = Area(1, Y) + Area(Y, XY)$. By then subtracting $Area(1,Y)$ in both sides of the equation above, the equation to prove then becomes $Area(Y, XY) = Area(1,X)$. That’s the equality of the green and blue areas!
But you’re not done yet…
Compare them!
Exactly! The blue area is horizontally $Y$ times longer! What about vertically?
Bingo! Here’s a figure of the operations you are talking about!
I know! That’s why the primitive of $1/x$ is a logarithm! It’s known as the natural logarithm, and is commonly denoted $\ln x = Area(1,x)$. The base of this logarithm is a weird number though, called Euler’s number in reference to the great mathematician Leonhard Euler. It is commonly denoted $e$ and is approximately $e \approx 2.7$. It stands for the solution to the equation $Area(1,x) = 1$.
You should try to figure it out yourself!
To find out how to change base, you can simply play around with formulas. Eventually, you’ll obtain $\log_c x = \log_b x / \log_b c$. Thus, in particular, $\ln x = \log_{10} x / \log_{10} e$.
Power Series
Historically, the invention of logarithms was accompanied with the first studies of infinite sums, also known as infinite series. In particular, power series were to provide deep insights into common diverse functions, including logarithms.
A power series is an infinite sum of terms $a_n$ multiplied by $x^n$. We write it $\sum a_n x^n$, and it sort of means $a_0 + a_1 x + a_2 x^2 + a_3 x^3 + \ldots$, and so on to infinity. But, as you can read it in my article on infinite series where I explain why $1+2+4+8+16+… = -1$, infinite sums can be tricky!
Amusingly, any of the usual functions we use can be written as a power series. The function is then uniquely identified by the terms $a_n$ of the series of $\sum a_n x^n$. And this is the case of logarithms! Sort of…
Well, actually, the function we should try to write as series is rather $\ln(1+x)$… So, without further ado, let’s find the terms $a_n$ corresponding to $\ln(1+x)$!
First, we write $\ln(1+x) = \sum a_n x^n$. Then, we’ll use the differential properties of the natural logarithm we have found out earlier.
Yes! This means that if we differentiate the natural logarithm, we should obtain is $1/x$. Now, if you remember your courses of computation of derivatives, you should now be able to compute the derivative of $\ln(1+x)$!
Excellent! Now, let’s find the power series of $1/(1+x)$! The key is for you to remember (or learn about) how to calculate sums of geometric series…
Let me redo the calculation then… We have $\sum x^n = 1 + x^1 + x^2 + x^3 + \ldots = 1 + x(1+x+x^2+ \ldots) = 1 + x \sum x^n$. Therefore, $(1-x) \sum x^n = 1$, and $\sum x^n = 1/(1-x)$.
To get from $1/(1-x)$ to $1/(1+x)$, we just need to replace $x$ by $-x$! This gives us $1/(1+x) = 1/(1-(-x)) = \sum (-x)^n = \sum (-1)^n x^n$. That’s a power series!
We have $\ln(1+x) = \sum a_n x^n$. If we differentiate both sides, we now have $1/(1+x) = \sum n a_n x^{n-1}$. Arranging both sides then yields $\sum (-1)^n x^n = \sum (n+1) a_{n+1} x^n$. Thus…
Yes, or, by replacing $n+1$ by $n$, we have $a_n = (-1)^{n+1}/n$.
We can now write $\ln(1+x)$ as a power series!
Well, sort of…
Sadly, you won’t be able to compute $\ln 3$ with this formula, as the power series does not converge for $x=2$! It just gets bigger towards plus infinity and minus infinity alternatively! In fact, as displayed in the animation on the right where terms in the power series are added sequentially to get closer to the actual value of $\sum a_n x^n$, the equality will only hold for logarithms of values between 0 and 2! That’s the horribly everlasting trouble of power series!
Complex Calculus
Still, an amazing empowering of the expansion of $\ln(1+x)$ in infinite series is the possibility we now have to define logarithms of complex numbers! Indeed, for any complex number $z$ whose module is smaller than 1, the series $\sum (-1)^{n+1} z^n/n$ converges, and defines a value for $\ln(1+z)$.
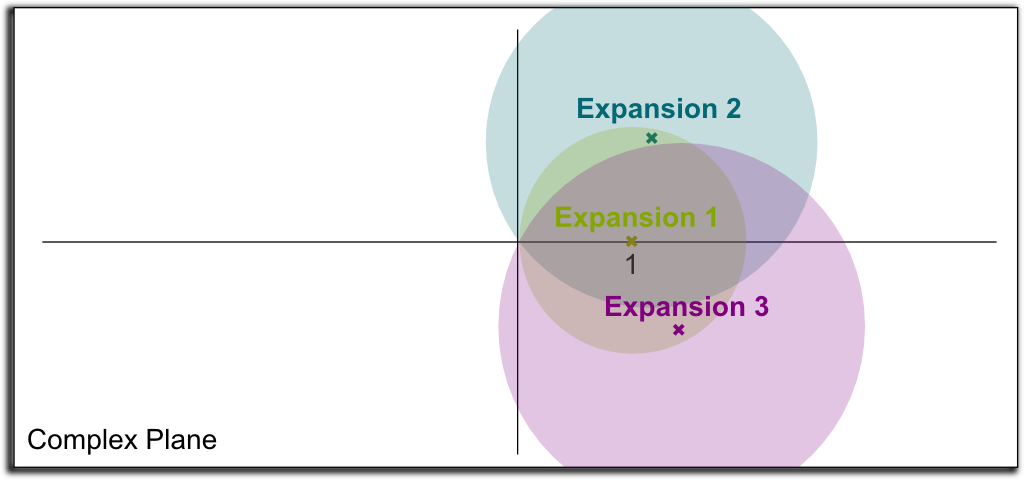
Indeed, the values $1+z$ for $|z| <1$ is a disk centered on $1$ and of radius 1. But, amazingly, we can then write the power series of $\ln(c+z)$, for any $c$ such that $\ln c$ has been defined! In another disk now centered on $c$, this will define new values for the complex logarithm $\ln z$! By doing so, we will have expanded the domain of definition of the natural logarithm in the complex plane.
An example of three first steps of expansions is pictured below:
By continuing this on to infinity, we can now define the logarithms for nearly all points in the complex plane! This amazing technic is known as analytic continuation.
Some points will be unreachable no matter how hard we try to expand the analytic continuation. But in the case of the logarithm, the only unreachable point is $0$! We say that $0$ is a pole of the natural logarithm.
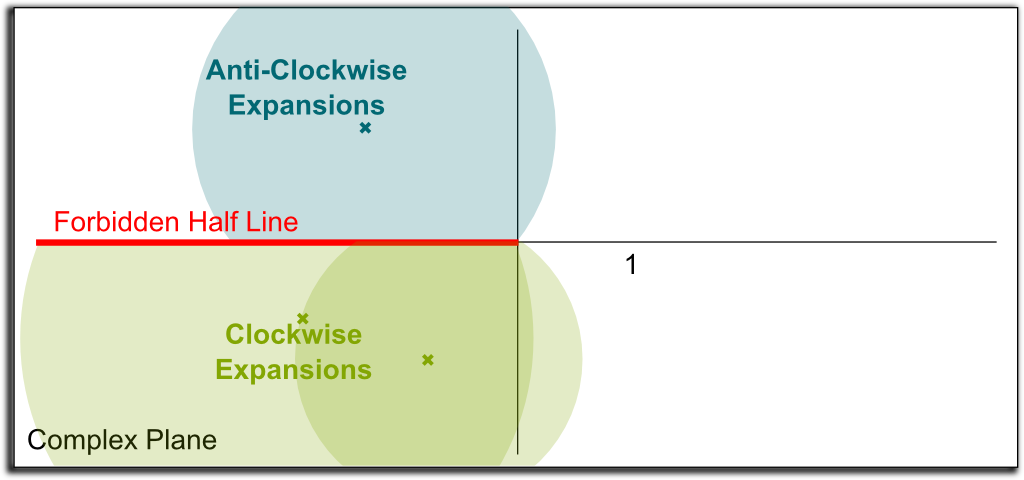
Unfortunately, yes we can… The thing is that each expansion is valid locally. Each expansion is in agreement with the expansions of its neighbors. However, as we turn around the origin, we have some expansions which have been built from a clockwise expansion of the original expansion around the origin, while others have been built anti-clockwise. These two kinds of expansions won’t agree. This fundamental result says that the natural logarithm cannot be uniquely expanded to the whole complex plane!
Exactly! The natural logarithm is actually defined up to $2i\pi$! That’s why Bernhard Riemann had the brilliant idea of defining the natural logarithm on a sort of infinite helicoidal staircase rather than on a complex plane. This staircase is known as the Riemann surface of the natural logarithm, and is explained by Jason Ross in the video extract below:
To provide a nearly natural well-defined natural logarithm in the complex plane, mathematicians often choose to cut it along a forbidden half line starting at the origin. Typically, the half line of negative number is chosen, and we choose the determination of the logarithm which yields $\ln 1 = 0$. Then, we apply the analytic continuation, but we forbid an analytic continuation to cross the forbidden half line. These restrictions ensure that the expansion of the natural logarithm to the complex plane minus the forbidden half line is well-defined and unique. This is what’s pictured below:
The natural logarithm we obtain by doing so is such that $\ln z$ always has an imaginary part in $]-\pi, \pi[$. It is known as the principal value of the logarithm.
Let’s Conclude
The take-away message of this article is that logarithms are a hidden structure between multiplications and additions. This is the fundamental property of logarithms, and it has many direct applications in computations, calculus and information theory. And age counting… An important implication of that property is the fact that logarithms can capture the size of huge numbers by small ones. This has plenty of applications to measurements in physics and chemistry. It is also essential to describe growths, like in the prime number theorem.
Finally, since we have defined logarithms for complex numbers, let’s mention what happens if we try to define logarithms for other sorts of numbers. In particular, in modular arithmetic, the logarithm modulo $p$ base $b$ of $n$ is naturally defined as the power $x$ such that $b^x$ is congruent to a certain number $n$ modulo $p$. If $p$ is prime, then this logarithm is well-defined. However, computing $\log_{b,p}(n)$ is considered as a difficult problem, and is thus an interesting property for cryptography. This is what’s explained in this great video by ArtOfTheProblem:
Finally, I can’t resist showing you a surprising connections between logarithms and newspaper digits. More precisely, between logarithms and first digits of newspaper numbers. This mind-blowing connection is known as Benford’s laws… Well, I’ll just let James Grime explain it to you!
What Benford’s law hints at is that age isn’t the only measure which should rather be quantified with logarithmic scales…



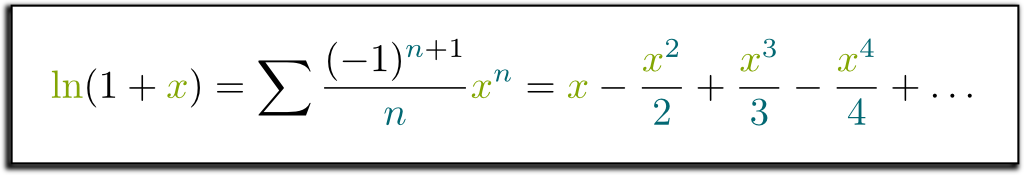
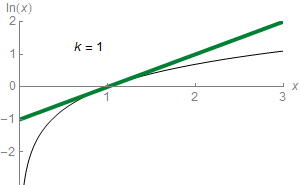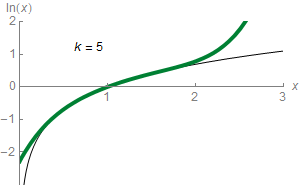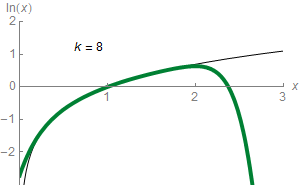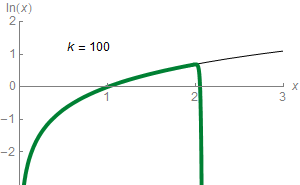
Leave a Reply