Last summer, at the EURO/INFORMS conference in Rome, Professor George Nemhauser religiously praised the last 50 years of integer programming. Since 2000, this powerful mathematical theory has been applied by 53% of Franz Edelman prize finalists! This means that half of applications of mathematics to real-world problems involve integer programming, making it the greatest pinnacle of the whole of applied mathematics! Thus, to the question is mathematics even useful?, most answers probably should include integer programming…
This is something I propose to fix now!
Some Applications
Before actually talking about integer programming, let me get you excited about it by reviewing three important classes of problems integer programming solves, and a fraction of their uncountable applications to our every day world!
Yes! Today’s technologies are now filled with optimizing processes, many of which involve the cleverness of integer programming. Here’s an awesome video that explains that:
Find out more about operations research by checking other videos of the Youtube channel LearnAboutOR! Let’s go a bit more into details…
Set Partitioning Problem
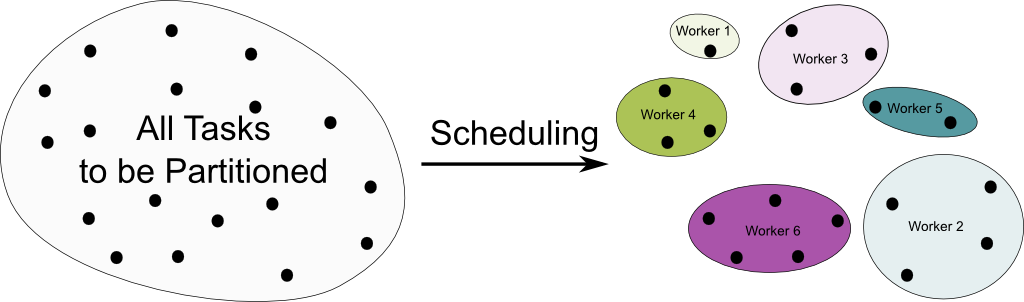
The most important class of problems is probably the class of set partitioning problems. A key application of these is the scheduling problem. This problem consists in defining a plan to carry out a set of tasks. Typically, these tasks will have to be given certain number of workers. In other words, tasks must be partitioned among workers, as in the example below:
Finding such a partitioning isn’t much of a problem, but finding the optimal one is. And this is particularly the case when you have additional constraints! For instance, some workers may be more qualified than others for certain tasks, some tasks might have to be done one after the other (for instance the packaging must be done before the delivering of the good) and some may be incompatible with one another (one can’t be at the warehouse and delivering a good at the other end of the city all at once)… More importantly, there might be so many workers (like 5, 6 or 152!) that it would no longer be possible for you to keep track of what each and every one is doing. At this point, using integer programming will provide you a much more efficient management of employees and tasks!
Yes! But not only for managers! Set partitioning has plenty of other applications. In particular, it is widely used by airline companies to design the routes of their planes. Each destination may then be considered as a task, and the airline companies will then have to partition destinations among their planes. Other examples include vehicle routing for pick-up and/or delivery, data mining used for instance in marketing to characterize classes of customers, scheduling baseball or soccer games for the season, designing wedding dinner tables… More amusingly, my professor used to apply set partitioning to sort out who voted what, given the result of a secret company board vote!
Facility Location Problem
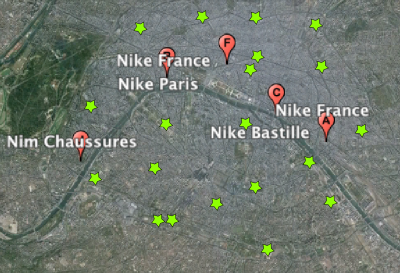
Another important class of problems that integer programming efficiently faces is the facility location problem. Imagine you were a manager of Nike and wanted to open several new stores in Paris. What you can do is gather a few candidate locations for your stores. But then, you need to choose only a subset of them to be actually built! The chosen locations must fit the populations of the city, but also and less obviously, they must be well selected with regards to one another! You don’t want them to all be grouped in a single location!
You can do much better with mathematics than with your brain only! That’s because of the combinatorial inter-dependence of the locations of your stores, which is very hard to analyze! For instance, in our very simple example, there are already over a thousand ways to choose the locations of three new stores!
Yes! As you can imagine, any problem of choosing the location for a new facility can be solved similarly. For instance, Google and Facebook recently had to solve facility location problems, as they were searching for where to build their latest data centers in Europe. But the facility location problem isn’t restricted to geographical location! A friend of mine is finishing his PhD where he studied where to locate virtual machines of applications running on the computing cloud! More generally, in telecommunication, the facility location problem often comes along with a network designing problems, which requires the full potential of integer programming to be solved efficiently!
Ordering Problem
The traveling salesman problem is an iconic problem of applied mathematics which belongs to a family of ordering problems. Here’s a short presentation of this problem I gave in my More Hiking in Modern Math World talk:
Basically, the traveling salesman problem consists in finding the cheapest itinerary that goes through a set of customers. Now, this can be equivalently restated as the problem of finding the right order in which to visit the customers. This problem is particularly important for theoretical reasons, as it has been known to be NP-complete.
Yes! And that’s because the number of ordering is just spectacularly huge! For only 60 customers, there are as many orderings as the number of particles in our whole universe! The awesomeness of integer programming is to address efficiently problems as complicated as the traveling salesman problem.
Sure! For instance, they come up in supply chain management. More surprisingly, it’s also applied to DNA sequencing! And I’m sure that we have only made the first steps in a endless range of applications ordering problems can have! As more and more complex systems are modeled with more and more powerful mathematical frameworks, I strongly believe that the most astonishing applications of integer programming have yet to be discovered!
Linear Relaxation
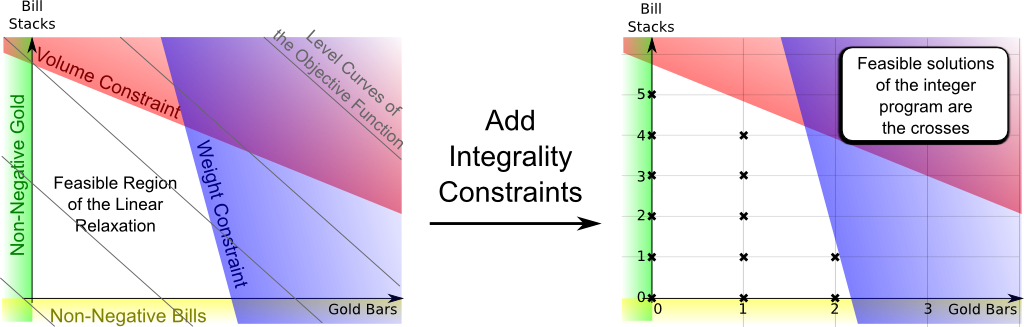
To present the technics of integer programming, let’s take an example. And I’ll use a slight variant of the smart robber problem I used to introduce linear programming, duality and the simplex methods. In this problem, a robber can either steal gold or bills, but he is limited by the volume of his bag and by the weight he can carry.
We’ll now assume that each piece of gold comes as a heavy gold bar. Similarly, bills are given in huge stacks.
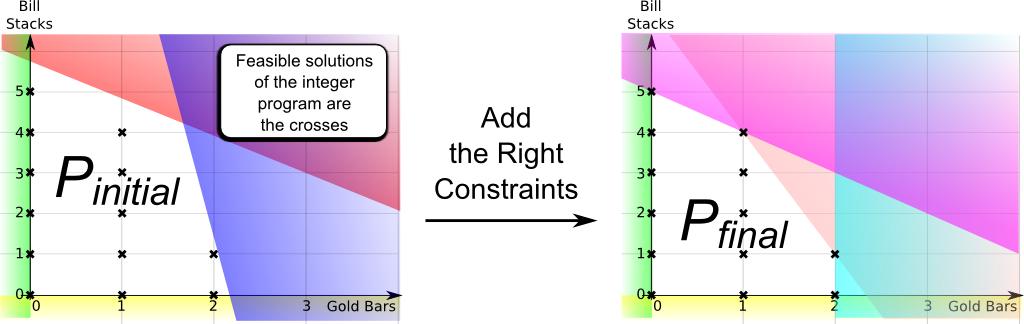
It means that we cannot have any amount of gold we want, nor can we have any amount of bills we want. We can only work with an integer number of gold bars, and with an integer number of bill stacks. As a result, only integer values of the feasible region are feasible. This is what’s illustrated below:
Below is the formulation corresponding to the figure above, where constraints are matched with colors accordingly. Formally, the integer program is simply obtained by adding the purple integer constraint:
Surprisingly, it’s quite the opposite! The integrality constraint breaks the beautiful linear structure which made the problem efficiently solvable. As it turns out, the strongest asset we have to face integer programming is precisely its similarity with linear programming! In fact, an integer programming worthy of that name is an optimization problem where variables are integers and which has a linear structure. The linear program obtained by withdrawing the integrality constraint is then called the linear relaxation.
One point is to provide an upper bound on the optimal value of the integer program. Indeed, because there are many more feasible solutions in the linear relaxation than in the integer program, the optimal value of the linear relaxation is always better than the optimal value of the integer program itself. The difference between these two values is known as the integrality gap, and it sort of represents how much harder the integer program is, compared to its linear relaxation.
No, indeed. However, any feasible solution of the integer program yields a value for the objective function which will be a lower bound. And what’s usually done in integer programming is an attempt to increase the lower bound and decrease the upper bound to better know the actual optimal value of the integer program. In particular, if these two bounds end up meeting, then their common value is the optimal value of the integer program!
There are two major technics to do so, known as cutting planes and branch and bound. In practice, a mixing of the two is used to reach greatest performances. Let’s discuss each in details!
Cutting Planes
The method I find the most beautiful mathematically is the cutting plane method.
Before getting to the cutting plane method itself, notice that, by adding the right linear constraints, any integer programming can be made equivalent to its linear relaxation. Such a case is called an ideal formulation. Below, the dark constraints are replaced by light colored constraints, hence making the formulation ideal:
The idea of the cutting plane method is to search for linear constraints which get us closer to the ideal formulation. Any linear constraint found is then called a cutting planes as it cuts the feasible polyhedron along a hyperplane (although, in our case, in dimension 2, they are simply cutting lines…)!
Yes! Here’s why. If the integer program has a linear structure, then its feasible points are all the integer points of the polyhedron $P_{initial}$ of the initial linear relaxation. Now, let’s consider the convex hull of the feasible integer points. We’ll show that this convex hull defines the ideal formulation of the integer program.
The convex hull is the set of all points which are in-between the feasible integer points. It forms a convex polyhedron $P_{final}$ inside the initial convex polyhedron. Since it is a convex polyhedron, it corresponds to a linear program.
Yes! Here’s why. First, since this convex polyhedron $P_{final}$ is included in the initial convex polyhedron $P_{initial}$, all integer points of the $P_{final}$ are obviously integer points of $P_{initial}$ too. What’s more, by construction, $P_{final}$ contains all feasible points of the integer program. Thus, integer points of $P_{initial}$ and $P_{final}$ coincide! Second, still by construction, all extreme points of $P_{final}$ are integer points. Thus, any optimal solution given by simplex methods will be an integer feasible solution! That’s why the linear relaxation is equivalent to the integer program!
Yes! At least, theoretically…
Actually, no. The Gomory-Chvatal cutting plane method yields a systematic way to generate right cutting planes. In practice, in many problems, there’s even a direct way to compute all the right cutting planes. Thus, in general, the problem isn’t our ability to construct the equivalent linear program…
The problem is usually that the number of cutting planes required to construct the equivalent linear program is exponential! This means that the list of constraints may not even fit in the memory of the computer, and, even if it did, the simplex method would then be extremely slow…
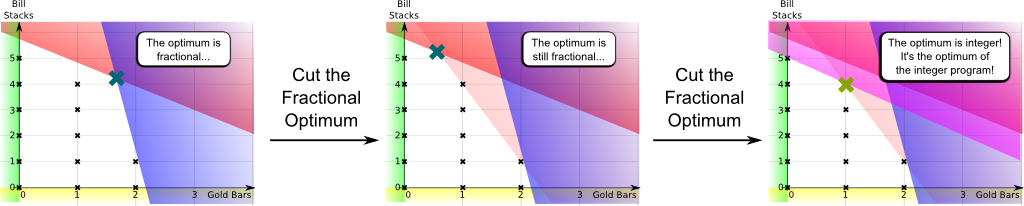
What’s interesting is that listing all the required cutting planes is not necessary for the integer program to be equivalent to its relaxation! In practice, we first solve the linear relaxation. If the optimum found is integer, then it’s optimal for the integer program too! Otherwise, it’s fractional. Then, we add some linear constraints which cut this fractional solution out of the feasible polyhedron. This yields a better linear relaxation to work on! And we can then repeat this cutting plane method on this improved linear relaxation until an integer optimum is found! This is the case illustrated below:
A key remark to be made here is that the cutting planes are interesting only locally, so a cutting plane may later become useless. Thus, in general, a right management of these cutting planes is key to solve efficiently the integer program.
However, in most cases, the best strategy is still to couple cutting plane methods with the powerful branch and bound method!
Branch and Bound
The branch and bound is sort of a divide and conquer method.
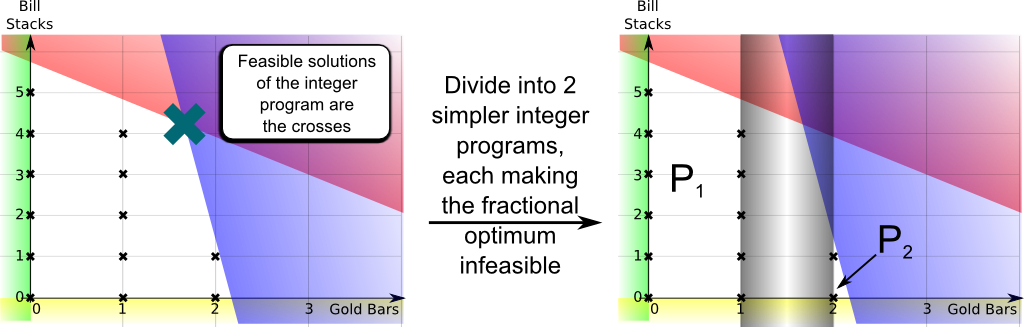
It consists in dividing the integer program into two much simpler ones. For instance, in our case, we can work separately on the case where the number of gold bar stolen is smaller or equal to 1, and the case where it’s greater or equal than 2! Each of the cases simply corresponds to adding a linear constraint, either $n_{gold} \leq 1$ or $n_{gold} \geq 2$. Each case defines a new integer program corresponding to one of the polyhedra $P_1$ and $P_2$ depicted below:
Technically, we say that we are branching onto two simpler integer programs.
Yes! The key point of the branch and bound is to enable us to delete the middle grey band from the optimization problem, which makes each of the 2 obtained integer programs much easier to solve than the initial one. The optimal value of the initial integer program then equals the best of the optimal values of the 2 branched integer programs.
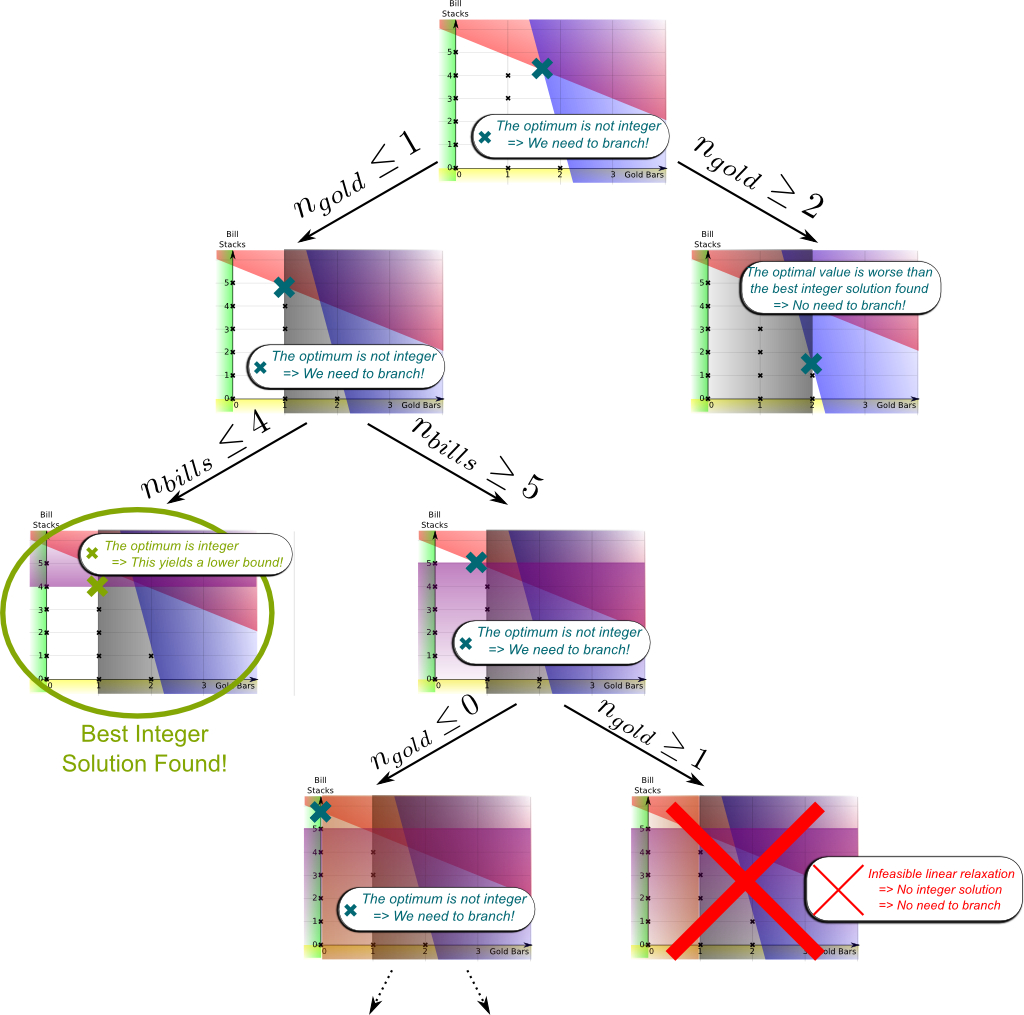
You’re right! More often than not, one branching is not enough. Each branched integer program then gets branched itself, until the optima of the branched integer program are integer solutions… or until we find out that the branched integer program has no feasible point! This is represented by the figure below, which depicts what we call the branching tree:
Each linear relaxation can either have an integer optimum, a fractional optimum, or no feasible solution. These cases are depicted by green, blue and red crosses.
In the green case, when the optimal solution found is integer, we have found a integer solution of the initial program. Thus, its value is a lower bound of the initial integer program! Plus, since the green solution is the optimum of its branch, there’s no need to do any exploration of the branch anymore.
Let me now address the red case which is simpler than the blue one. In the red case, there’s no feasible solution to the linear relaxation. Thus, obviously, there’s no solution to the integer program either. Thus, the branch explored is completely useless and we can just drop it.
That’s the bad news case, as it means that the corresponding integer program is not equivalent to its linear relaxation! The only chance of good news is if the optimal value of the linear relaxation, which is an upper bound of the corresponding integer program, is lower than the best lower bound we have found with green solutions. Then, we can deduce that there’s no need to explore subbranches, as they won’t provide a feasible integer solution better than the best we have found so far! This remark corresponds to bounding and enables to greatly speed up the branch and bound method. It’s what happened to the branch on the extreme right.
Then its branches still might have a better integer solution than the best one found so far… So we need to keep branching!
Let me finish this section with one last major remark. In branch and bound methods, there’s a freedom in which next branch we are going to focus on. There are two extreme possibilities. On one hand, we can explore in depth the first branches we generate. The major advantage is that this enables to quickly find a feasible integer solution, which can be returned even if the algorithm stops halfway. The drawback though will be the quality of the lower and upper bounds. Basically, searching in depth also means that you are focusing on a particular kind of solution, as you rule out most of the other possibilities. A contrario, if you’re searching for a faster way to find as soon as possible the actual optimum of the integer program, you’ll probably be better off exploring in breadth, that is, line by line.
Let’s Conclude
To conclude, I want to stress the extraordinary accomplishments there have been in integer programming over the last decades. Within 20 years, the speed of integer programming solvers has been increased by an astonishing factor of 250,000! Can you believe that? And this doesn’t even include the increasing computational power of the computers! In other words, any problem we were able to solve using a 20-year old computer in 7 years can now be solved with this same old computer in just 1 second! Even more impressively, in comparison, the speed up of hardwares according to Moore’s law has been improved by only about 10,000 within the same period! These figures must be taught to anyone who doesn’t value research enough!
The most astonishing part is that this improvement in our algorithmic technics doesn’t seem to be slowing down! It seems impossible right now to even imagine what will be possible within the next decades! Too often, people forget that we live at an unbelievable time where new technologies improve at an exponential rate. As I try to make sense of that, many of the political debates seem deprecated to me… or about to be deprecated!
Hard to say… A lot of mathematicians are currently working on stochastic programming and column generation, which are clever technics based on the idea that solving an integer program doesn’t require it to be fully stated. By working on increasingly faithful approximations of the integer program, the actual optimum can then be found much quicker! Yet, the problems these technics address still suffer the curse of dimensionality. That’s why stochastic programmings when applied to complex problems tend to be replaced by robust linear programmings, which restrict themselves to searching for the best solution in worst-case scenarios. Finally, two hot topics in integer programming like, in any field of applied mathematics, are parallelization and machine learning. It’s particularly hard to even guess what will come out of these two topics…


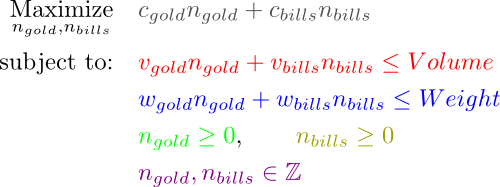

Leave a Reply