Self-reference is (too?) common in real life, as many of our sentences begin with I. Talking to persons who abuse of self-references can be tiring. And in mathematics, watching at self-referencing objects has turned into a nightmare, starting with British mathematician Bertrand Russell. In 1901, based on a reasoning on such objects, he proved that mathematics were non-sense.
No! Let’s see how he did it!
Russell’s Paradox
Bertrand Russell actually worked with the most fundamental mathematical objects: sets. Sets are simply collections of other mathematical objects. In very fundamental mathematics, sets are actually the only objects. So, really, what sets are is a collection of sets.
Let’s do the reasoning with Science4All articles to make it less abstract! I’ll replace the phrase “a set contains another set” by “a S4A article contains a link towards another S4A article“. Even more simply, we’ll say that a S4A article points to another S4A article. We can now apply Russell’s exact reasoning.
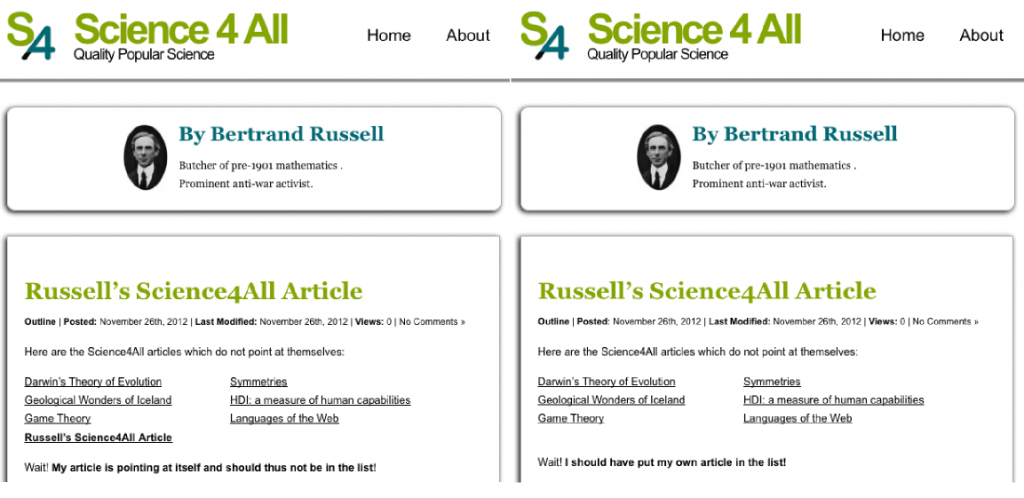
Now, there’s a simple self-referencing concept about S4A articles: A S4A article either points to itself or not.
Well, let’s consider the article you’re currently reading. This is a S4A article. And it has the following link towards itself (hover or click to verify that it really is the case!). So it points to itself. But most of other articles don’t point to themselves.
Good. Because we are getting to Russell’s great idea. He imagined himself writing a S4A article which points at all S4A article which don’t point to themselves. Let’s call this article Russell’s S4A article.
The S4A article called Self-Reference you’re currently reading points to itself, so Russell’s S4A article wouldn’t point to Self-Reference. But most of other S4A articles don’t point to themselves. Russell’s S4A article would point to them.
As Russell writes it, he has to choose whether his S4A article will point to itself! Think about it. If it does point to itself…
Yes! But if it doesn’t point to itself…
Yes!!! Let’s recapitulate with the following figure:
Exactly! Yet, mathematics at Russell’s time allowed to construct such theoretical S4A article… which means that it allowed the existence of something that doesn’t exist! No wonder why 1901 mathematics was non-sense!
More generally, Russell’s paradox consists in replacing the verb contain by any other verb. Here are some similar paradoxes we can obtain by doing so:
- Imagine a barber who shaves everyone who doesn’t shave themselves. Does he shave himself?
- Imagine a painter who paints everyone who doesn’t paint themselves. Does he paint himself?
- Imagine a blogger who blogs about everyone who doesn’t blog about themselves. Does he blog about himself?
Another example of similar paradoxes is the following extract from The Office.
There are lots of puzzles based on self-referencing. Here’s a nice one. Assume you are faced with two doors. One leads to heaven, the other to hell. But the only way for you to know is by asking one single question to the angel in front of you… who may in fact by the devil. The thing is, if he’s an angel, he can’t lie, but if he’s the devil, he has to lie. What question should you ask?
Think about it. I’ll give the answer at the end of this article.
It is bad! It is extremely bad! Because one contradiction in mathematics imply that all mathematics is non-sense! Think about it. A lot of reasonings in mathematics are based on reductio ad absurdum: You start by assuming something and show that this assumption implies a contradiction. This proves that what you assumed is wrong. But now, you can assume anything, like for instance that 0=0, and say that it leads to Russell’s paradox. This mathematically proves that 0≠0, which in turn can imply something like 1=0. Russell’s paradox proves that mathematics in 1901 was non-sense!
It was! This image from the awesome graphic novel Logicomix, which narrates the foundation crisis in mathematics in early 1900s through the story of its main contributors, depicts Russell’s stupefaction when he discovered the paradox:
At this point, Russell knew that everything in mathematics and logics was destroyed!
Just like you, mathematicians of the beginning of the 20th century, including Gottlob Frego and David Hilbert, were devastated! So they rejected classical assumptions of mathematics, now known as the naive set theory. And they searched for a better-defined formalism. And the 20th century has produced incredibly surprising and counter-intuitive results regarding such formalisms. For instance, they enable to prove that $1+2+4+8+16+…=-1$, as you can read it in my article on infinite series! But there’s even more troubling… Since it’s a little complicated, I’ll get to this in the third section of this article.
Recursion and Fractals
What I’m now going to show you is that self-referencing isn’t all bad. As long as it’s done properly…
One extremely useful self-referencing in computer science is known as recursion. It is based on the idea that if you can break down your problem into simpler versions of itself.

Let me give you an example. Consider a chocolate bar, the kind of which is made of well-ordered squares. like the one on the right. Now, imagine a bar with $2 \times n$ squares. But your kids or students only like to have $1 \times 2$ pieces of chocolate. How many ways are there to divide your bar into $1 \times 2$ pieces of chocolate?
The following figure displays 6 different ways to divide a $2 \times 6$ bar of chocolates into $1 \times 2$ pieces.
How many ways are there in total?
No. I want you to find the answer without counting! And it’s possible, thanks to the magic of recursion!
Yes!
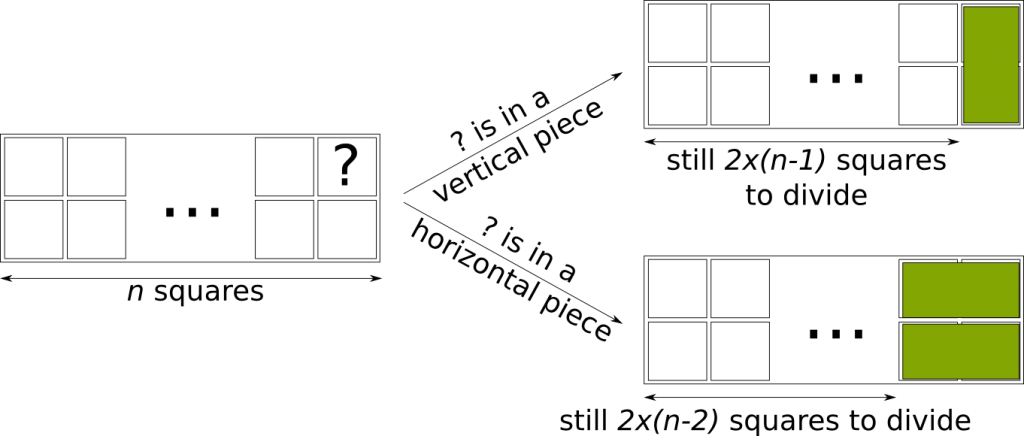
Sure. Look at the top right corner square of your bar. It needs to belong to a $1 \times 2$ piece. But there’s only two possibilities for this piece: It’s either horizontal or vertical. Now, if it is vertical, then you end up with a $2 \times (n-1)$ chocolate bar! That’s a smaller version of this problem!
Well, if it is horizontal, you have to notice that the two pieces below the horizontal piece must be grouped into another horizontal piece. And you are left with filling…
Yes! Let’s recapitulate with the following figure:
So, in one case, the number of ways to divide the chocolate bar is the solution of the problem for $n-1$. In the other case, it’s the solution for $n-2$! Overall, the solution for $n$ is the sum of the solution for $n-1$ and $n-2$. So if the solution for 4 is 5 and the solution for 5 is 8, then the solution for 6 is 5+8=13. And such reasoning can very easily be written as an algorithms for computers!
Our reasoning is actually incomplete. If we simply tell the computer to search for solutions $n-1$ and $n-2$ to solve the problem for $n$, we will have a big issue: Our computer will be searching solutions of -1 and -2 to find the solution of 0, and then search for solutions of -3 and -4 to find the solution of -2… and so on! To avoid this, we need a base case, that is, a case which does not depend on any other case. Well, in fact, here, we need two base cases, since we search for solutions at both $n-1$ and $n-2$.
Yes! A recursive algorithm is defined by base cases, and, for other cases, relations to other simpler cases. By simpler, I mean, cases which are strictly closer to base cases.
Sure! The most famous ones are probably Euclid’s algorithm to find the greatest common divisor, the solution to the tower of Hanoi and the state-of-the-art optimization technic called dynamic programming.
And it’s not limited to algorithms! A typical example of recursion in a definition is the following definition of ancestors: An ancestor is either one of your parents or an ancestor of your parents. Note that the base case here is a little hidden: The recursion relation is only defined if one actually has parents… This means that the base case is about people without parents! But do they exist? Well, that’s a tough conundrum of Darwin’s theory of evolution…
It is! But there’s something even better! In mathematics, you don’t necessarily need base cases to define recursion, as long as the simpler cases are “much simpler”! This amazing remark led to the construction of the wildest mathematical objects such as the Cantor set, the Kock snowflake and the Mandelbrot set. These objects are obtained by repeating their global appearances at lower scales of themselves. They are commonly known as fractals. They are probably the most beautiful creation of modern mathematics, with surprising applications in a large variety of fields, including biology, seismology, stock market analysis, information technology… and even in cinematography! Check this extract from Marcus du Sautoy’s show on shapes made with BBC:
Find out more, by reading Thomas’ great article on fractals to know what they really are! You should also check this great video to find out more about applications.
Gödel’s Incompleteness Theorems
Let’s now get back to the problem of the inconsistency of mathematics.
Yes. But remember how bad things were at its beginning: Mathematics were proven to be non-sense! From 1910 to 1925, to set mathematics straight, Bertrand Russell and Alfred North Whitehead wrote and rewrote the Principia Mathematica. It redefined new rules of mathematics, called axioms. The list of these axioms forms what is known as a theory. Russell and Whitehead’s theory aimed at forbidding self-referencing.
A few years later, in 1931, one of the greatest mathematician of all time, Kurt Gödel, reacted. He claimed that Russell and Whitehead hadn’t managed to forbid self-referencing. In fact, any theory which is interesting enough to include basic mathematics like natural numbers cannot forbid self-referencing!
He actually constructed such a phrase. Its construction is a little bit complicated. It’s based on a mapping of symbols of maths with numbers. This gives you a set of digits. A theorem is then a succession of such symbols. It therefore corresponds to a number made of digits. In fact, each theorem corresponds to a unique number. And, similarly, so does each proof. These numbers are called Gödel-numbers. Now, I’m not going go into the details, but Gödel proved that Gödel-numbers could be manipulated such that one could be eventually created such that it talks about itself.
Well, loosely stated, it says that there is no proof to itself. That’s Gödel’s amazing construction! Out of any theory interesting enough, the following phrase exists: The theorem you’re reading has no proof.
Worse than this! The self-referencing phrase I have given cannot be proven false nor true! If it is true, then you should have a proof. Yet, it says that there is no proof. On the opposite, if it is false, this means that it has a proof. But a theorem that has a proof is true! So unless the theory is inconsistent in which case a theorem can be true and false, Gödel’s phrase is neither true nor false! Such a phrase is called undecidable.
That’s pretty much Gödel’s first incompleteness theorem! Roughly, it says that consistent theories are necessarily incomplete.
The greatest illustration of this surprising theorem is the astonishing continuum hypothesis I explained in my talk More Hiking in Modern Math World.
I have never said that! What I said is that if they are consistent, then they are incomplete. But we’re not even sure they are consistent. We haven’t proven the consistency of mathematics!
Yes!
Surprisingly, no! Once again, that’s because of Kurt Gödel. Indeed, he also proved that theories can never prove themselves consistent! After all, a theory which talks about its consistency, that’s very much a self-reference!
It is possible for a theory to prove its inconsistency. But if there is no proof of its inconsistency, then there’s also no proof of its own consistency. This is known as Gödel’s second incompleteness theorem. Check this extract from my talk A Trek through 20th Century Mathematics where I present both Russell’s paradox and Gödel’s second incompleteness theorem!
Let’s Conclude
As opposed to what mathematicians thought 100 years ago, self-referencing is not bad at all! It’s an essential part of theories. And if done nicely, it can provide an extremely nice framework, like for recursion and fractals. In fact, self-reference is an essential part of some wonderful pieces of art. Think about Abed referring to TV shows in the TV show Community and Stargate SG1’s 200th episode, the classic movies usual suspects and fight club, or novels like Frankenstein and Le dernier jour d’un condamné (sorry I’m not that familiar with non-French classics). This technic in arts is commonly known as the mise en abyme (here’s a little bit more of French for you to learn!). Here’s one great example by Vihart, about herself making videos:
Oh yeah, that’s right! It’s in the food for thoughts below!




Leave a Reply