In our last two posts, on Euclidean Geometry and Navigation and Non-Euclidean Geometry and Map-Making, we’ve explored some of the key differences between geometry on a flat surface and geometry on a sphere. We concluded that, given these fundamental differences, it is impossible to create a perfect flat map of the Earth – any map you create will necessarily have some distortions or imperfections.
Yes, we’re fooled by our perspective on the Earth’s surface. If we fly into space it’s obvious the Earth is not flat. Amazingly, we don’t have to look at the Earth from outer space – or even resort to looking at its shadow on the moon – to determine that it has a curved surface. Tools developed by mathematicians working in the field known as “Differential Geometry”, make it possible to determine that the Earth is not flat simply by taking measurements on its surface.
These mathematical tools were in turn generalized to abstract, higher-dimensional surfaces sitting “inside” higher-dimensional spaces – and enabled physicists such as Einstein to develop accurate models of the geometry of space-time. Physicists in turn used this mathematical formulation to refine our understanding of gravitation. In this post we’ll explore the mathematical ideas underlying these key discoveries in 20th-century physics.
A glimpse into Differential Geometry
“Intrinsic” and “Extrinsic” points of reference
Despite the fact that the Earth is round, it appears to be flat, because of our relatively small size and position on its surface. In the same way, an ant walking on a large, round oil pipeline has the impression that it is walking on a flat surface. To a small creature on the surface of either of these objects, the surface appears to be flat. Check out this NASA image from the surface of the moon, whose surface also appears flat from the viewpoint of someone standing on it.
In geometric terms, we call the view of an object from its surface the “intrinsic” point of view of the surface. The “intrinsic” view technically means the view from a completely flat object on the surface, not the view of someone standing on the surface, but in practice this distinction is irrelevant if the person is sufficiently small that they can only see a small region around where they’re standing. From the “intrinsic” point of view of a person standing on the Earth, an ant walking on an oil pipeline, and someone standing on the moon, each of these surfaces appears to be flat. In mathematical terms, we say that the surface of each of these objects is “locally Euclidean” – from the viewpoint at each point on the surface, the surface appears to be flat, like a table.
From the external point-of-view – what geometers refer to as the “extrinsic” point of view of a surface – the Earth, the oil pipeline, and the surface of the moon are clearly not flat. If you’ve ever flown on a jetliner, you’ve probably seen the curvature in the Earth’s horizon. Here’s a NASA image of the surface of one of Saturn’s moons, Rhea, from the extrinsic point of view, taken by the Cassini-Huygens spacecraft.
Keep in mind that someone on the surface of Rhea can’t detect this curvature – it appears flat from the intrinsic point of view.
Flatland
The classic work Flatland, by Edwin Abbott, published in Victorian England in 1884 CE, describes the life of 2-dimensional beings living in 3-dimensional space. The narrator, who is a square, describes life in Flatland – the more sides an object has, the bigger its angles are, and the smarter it is.
The narrator has a dream about life in a one-dimensional land called Lineland. He attempts to teach the inhabitants of Lineland about life in 2-dimensional Flatland, but finds it is impossible to get them to imagine life in more than one dimension. In another dream, he is visited by a sphere who teaches him that there is a third dimension, called Spaceland, and describes life in Spaceland.
From the point of view inside of Flatland, the idea of 3-dimensional space is impossible to imagine. Think about it: if the creatures of Flatland are only accustomed to life inside of 2 dimensions, they have no basis on which to imagine a 3rd dimension.
The narrator insists on teaching the inhabitants of Flatland what he has learned about Spaceland, and describes a third type of direction called “Upwards, not Northwards”. From the viewpoint of the Flatlanders, the narrator appears to be insane: again, they have no basis from which to imagine something like a third dimension. Ultimately, he is persecuted for his teaching, and is arrested and sentenced to prison.
The book was intended to provide social commentary on life in the uptight society of Victorian England, where many people held stale, traditional views about society, but has become well-known for its descriptions of geometric dimension. For this article, the important point is that, for someone living in Flatland, it is difficult or impossible for them to imagine that they are actually living in a space with more than two dimensions. Because they’re caught in the viewpoint of two-dimensional Flatland, the idea that there is a third dimension, “Upwards, not Northwards”, is impossible to comprehend.
“Flatland” was developed into a movie in 2007; you can see the entire movie on Youtube, or check out the trailer here:
More about “Intrinsic” and “Extrinsic”
Recall our definition of the “intrinsic” and “extrinsic” viewpoints of a surface. Up until the 19th century, geometers focused on studying geometry from the extrinsic point of view. Euclidean geometry, for example, studies the properties of objects that can be drawn on a sheet of paper using a straight-edge and a compass; it studies flat 2 dimensional space from our 3rd dimensional perspective. Despite the fact that the Earth is not flat, it is still possible to make fairly accurate calculations regarding Earth navigation using Euclidean geometry, since the Earth is “locally Euclidean” – in small regions, its surface is, for practical purposes, flat.
Importantly, Newton’s conception of mechanical physics was also founded in Euclidean geometry, and is thus based on geometry studied from the extrinsic viewpoint. This viewpoint of the Earth’s surface is accurate for most practical purposes, because a sphere is locally Euclidean – it looks flat from the viewpoint of a small person on its surface – but it does not offer a completely accurate description of the Earth’s surface, as we saw in the article on map-making.
In the following section we will see that the underlying curvature in the Earth’s shape leads to detectable and meaningful differences in measurements upon its surface. This implies that the “intrinsic” and “extrinsic” viewpoints of a surface are linked in a surprising way, and will prove useful as we see how Newton’s conception of the universe is mistaken, but still useful.
Before move along, you might check out this depiction of how a Flatlander would experience his or her flat world. The view described is the “intrinsic” view of Flatland, while the “extrinsic” view would study Flatland from the perspective of someone living in Spaceland.
The youtube user 10thdim also has a number of useful videos on the subject of dimension, such as “Imagining the 10th Dimension”, where he helps us to imagine higher dimensions using analogies from the lower dimensions. The concept of higher dimensions is useful for understanding general relativity, which describes space and time as a 4 dimensional fabric, as we shall see, and is also useful for understanding quantum mechanics and string theory, which imply that the universe has either 10 or 11 dimensions.
Gauss’s Remarkable Theorem
The key point that allowed us to advance our study of the Earth, and eventually improve our understanding of higher-dimensional spaces, was the move towards studying geometry from the intrinsic viewpoint, beginning with the mathematician Gauss. Gauss (pictured below, in 1828) found that the Gaussian curvature of a surface – a measure of how “curved” a surface is at a given point – can be determined by taking measurements directly on the surface, without taking into account the space in which it is embedded.
This is known as his “Remarkable Theorem”, since it can be used to show that a sphere is not a flat surface simply by measuring lengths and angles (and their rates of change) on the surface of the sphere; it’s not necessary to look at the sphere from an outside viewpoint in order to determine that it is not flat. The “Remarkable Theorem” arises from the fact that underlying curvature in an apparently flat surface causes noticeable differences in measurements taken while moving around its surface.
In fact, it’s also possible to detect rotation in the Earth using what is known as Foucault’s Pendulum. If you string a pendulum from a high ceiling, in such a way that it is free to swing in any direction (rather than simply left and right, as in a grandfather clock), the Earth will actually rotate underneath the pendulum, thus causing the pendulum’s path to take on what appears to be a circular shape. It is in fact swinging forwards and backwards, and the Earth is rotating underneath it. Check out this Dartmouth exhibition of how the Foucault Pendulum works.
Back to Gauss. With his Remarkable Theorem, he paved the way for the study of geometry from the “intrinsic” viewpoint, but his work dealt strictly with 2-dimensional surfaces lying in 3-dimensional space. In order to be applied to modern physics, his ideas needed to be generalized to higher-dimensional surfaces and spaces, and Gauss’s student, Giorg Riemann, did just this.
Riemann was able to extend Gauss’s results about two-dimensional surfaces sitting in three-dimensional space, to general higher dimensions. This intrinsic study of geometry turned out to be revolutionary for modern physics, since it served as a basis for Einstein’s insights regarding the “theory of relativity”, which shows how space and time are related as a 4-dimensional structure.
Einstein’s General Relativity
This is a subject that requires heavy mathematical machinery to fully understand, but I think we can get an idea of the basics of the subject without using complicated calculations. Have you read through Le’s article on special relativity? If you have, you’ll recall that special relativity describes certain refinements to Newtonian mechanics, and implies that time, mass, and distance become skewed when an object travels close to the speed of light.
After publishing his 1905 paper on special relativity, Einstein made a series of investigations on the properties of gravitation, which culminated in a 1915 paper giving a series of equations, known as Einstein’s Field Equations, which give a specific description of the structure of space and time, and how this gives rise to gravitation.
In Newtonian’s way of thinking about physics, gravity is considered a force that arises between two masses – a bit like magnetism – and makes them attract towards each other. Einstein, showed that gravitation is instead the effect of curvature in the 4-dimensional fabric known as space-time. Let’s take a more in-depth look at Newtonian physics to see how the discovery of general relativity came about.
A bit about Newton…
You’ve probably come across Newtonian physics in some form – when learning about gravity, levers, speed, velocity, and so forth. Newtonian physics assumes the world of space and time is structured a certain way. It assumes that there are three dimensions in space – forward/backward, right/left, and up/down, for example – and that time is independent of space and can be used as a parameter to make calculations about space. This works very well for most situations, such as measuring the distance a car has traveled, or weighing various objects using a scale, or setting up a gear-and-pulley system in the design of an elevator.
Check out this Youtube video, the first two minutes of which gives an excellent introduction to Newtonian physics.
Physicists knew that Newton’s conception of the universe worked well for modelling everyday activities, but had one central question about his idea of “gravity”: when two masses attract to each other via gravitation, how do they recognize each others’ presence? In other words, does gravitation happen instantaneously, regardless of the distance between the two objects, or is it like a wave, travelling at the speed of light?
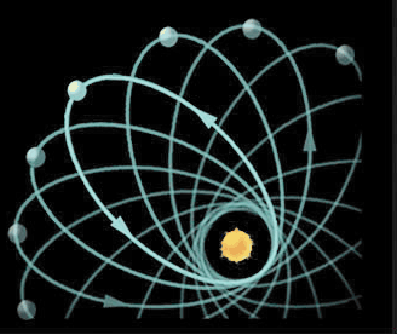
Another small problem with Newtonian physics arose in examining a property of Mercury’s orbit known as its perihelion procession. Mercury’s orbit, like all planetary orbits, has an elliptical shape, and the point at which it is closest to the sun, its perihelion, changes every time it flies around the sun. Astronomers measured this point over a number of years in the 18th and 19th century, and in 1859 were able to show that the behavior of its orbit did not match the predictions of Newtonian physics. Check out this depiction (from here of the shift in Mercury’s perihelion.
Note that the point at which Mercury’s orbit passes closest to the sun shifts every time Mercury flies around the sun. Astronomers measured the location of this point over many decades in the 18th and 19th centuries, and realized that Newtonian physics did not accurately describe the rate at which Mercury’s orbit shifted.
So Newtonian physics gave reasonably accurate equations for how gravity operates, but did not give a fundamental description for what gravity is and why it arises. It also gives reasonably accurate descriptions of the behavior of physics on Earth, but isn’t completely accurate, especially for large bodies travelling over large distances, such as Mercury. General relativity fills in the gap in both fronts. It gives a clear description of the nature of gravitation, and also gives equations that correct the inaccurate predictions of Newtonian physics.
Two crucial observations about gravitation
After his 1905 special relativity paper, Einstein began to think about gravitation, keeping in mind the problems with Newtonian physics we have seen. He realized that someone in the midst of free fall, such as a skydiver, would not experience themselves in a state of acceleration. From their perspective, they are at a standstill, and the rest of the world is decelerating (upwards). This observation – that the “force” of gravitation is experientially equivalent to the “pseudo-force” experienced by someone in an accelerating inertial frame of reference – forms what’s known as the equivalence principle.
Check out this NASA video from the Earth’s moon, in 1971. The astronaut drops a feather and a hammer, and both accelerate at the same rate. Since the moon does not have an atmosphere, there is no air resistance on the moon, and we can see that both objects accelerate in the same manner.
Again, the “equivalence principle” suggests that the “force” of gravitation is, from the perspective of each of these objects, experienced as an acceleration of their inertial frame of reference.
Around the same time he formulated his “equivalence principle”, Einstein also noticed an analogy between gravitation and curvature. An object moving at a constant momentum, in a frame of reference free of gravitational forces, will continue to travel in the same direction, with the same momentum, but if exposed to a gravitational field, its velocity will become accelerated. Einstein realized that gravitation acts like a kind of curvature, and “bends” the path of an object, in the same way that curvature “bends” a flat plane into a curved surface.
He also recalled reading through Gauss’s work on the curvature of surfaces, such as his “remarkable theorem”. At this point, he looked into the work of geometers such as Riemann and Ricci, and was able to formulate the basic ideas of general relativity. He realized that the mathematical structure known as a “manifold” – a smooth structure that appears to be flat from its surface – would serve as a useful mathematical model for space-time.
He suggested that space and time aren’t disconnected, as Newton suggested, but instead form a 4-dimensional structure known in mathematical terms as a “manifold” – a smooth structure that appears to be Euclidean – that is, flat – at each point on its surface. The “manifold” offers a perfect model for space-time, since at each point on a manifold, there is a local coordinate system arising at that point and specific to that point. Gauss and Riemann’s work on curved surfaces also gave Einstein a way to model curvature and space-time, and he suggested that space-time becomes curved around masses such as the sun. Check out this depiction of the curvature in space-time that arises at a mass such as the Sun.
Note that it is impossible to draw a picture of 4-dimensional space-time; it is only possible to create analogies with curvature in 3-dimensional space. So the video above depicts curvature in space-time as curvature in 3-dimensional space (like a ball around the Sun), when in fact the curvature is 4-dimensional in nature.
Some practical results of general relativity
Yes! This is the amazing point. Astronomers had known since 1859 that the perihelion procession of Mercury did not obey the predictions made by Newtonian physics, and Einstein showed that the behavior of Mercury arose due to the curvature in space-time occurring close to the Sun.
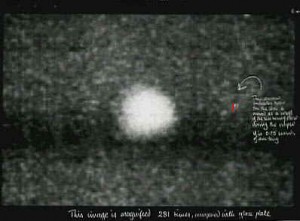
In 1919, astronomer Arthur Eddington also found that light from other stars actually bends around the sun in a way consistent with general relativity. This observation was made possible by a solar eclipse, which allowed the measurement of light passing around the sun. The results showed the light curved in a way consistent with general relativity and inconsistent with Newtonian physics. This caused a splash in the newspapers, since it was the first corroboration of relativity. Einstein’s general relativity became accepted at this time.
Here’s a picture, from here, of the star whose light was deflected by the sun. This observation showed that its light in fact curved around the sun in a manner consistent with general relativity, rather than Newton’s conception of physics.
Let’s go back to the thought experiment with the ant walking on the oil pipelines. Due to his position on the surface of the pipeline, the ant imagines the pipeline’s surface is flat. The ant can’t sense its curvature. In an analogous manner, Newton believed that space and time are independent of each other, and that time runs smoothly, in a linear, consistent fashion. This perception is due to our location on the “surface” of space-time – we are tricked into thinking that space and time are “flat” and independent of each other based on our position on the “surface” of space-time.
Einstein famously described common sense as the set of “collection of prejudices acquired by age eighteen”. His results regarding general relativity imply that our common sense ideas about the universe result from our position in the universe, and thus are skewed, in the same way that the ant on the oil pipeline has the mistaken idea that s/he is walking on a flat surface.
For example, we sense gravity as a force that arises between two masses. Based on our viewpoint, we don’t sense that gravitation is actually the result of curvature in the underlying space-time fabric. For this reason, gravitation occurs instantly. A mass curves the section of space-time surrounding it, by the simple fact of its presence. Two masses therefore attract to each other, not as a result of a “force” arising between the two, but due to the fact that their usual paths are deflected by the underlying curvature in space-time.
Well, as happens with many discoveries in science, it seems that Einstein and his cohorts came along at just the right time. Physics observations such as those involving Mercury were calling Newton’s assumptions about the nature of the universe into question, and ideas about the speed of light suggested also raised questions about the nature of gravitation – does it occur instantaneously, and if so, does this violate the notion that nothing can travel faster than the speed of light? At the same time, advances in geometry made it possible for Einstein to formulate his views regarding geometry and gravitation.
It’s not possible to picture, in our minds, curvature in 4-dimensional space-time. It took analogical thinking, and this required knowledge of both higher-dimensional geometry and modern physics. Check out this depiction of the curvature in space-time induced by a mass such as the Sun. Note that the “curvature” pictured in the video is simply an analogy of actual curvature in space-time; space-time is 4 dimensional and thus impossible for us to picture.
For most everyday applications of physics, Newton’s work is sufficient. When designing an elevator, you can simply assume that gravity behaves as Newton describes, and design your elevator using the physics derived therein. But for outer space technology, such as satellites, it’s necessary to take general relativity into account.
There are also astrophysical applications of general relativity. For example, the concept known as “gravitational lensing”, which describes how light bends as it passes near any mass in the universe, is used to indirectly detect dark matter in the universe. Dark matter isn’t directly visible with telescopes, but it can be indirectly observed by through its effects on light travelling from visible stars and galaxies. Astrophysicists who try to understand the nature and origin of the universe must take into account general relativity, but also can use effects such as gravitational lensing in their endeavours.
Excellent question! In this piece, we haven’t gone into the heavy-duty mathematics underlying relativity, such as the Einstein Field Equations, a set of coupled hyperbolic-elliptic nonlinear partial differential equations (whew!) which describe the curvature in space-time arising around a mass. They’re in turn based in tensor calculus and Riemannian geometry, mathematical machinery that provides a natural way in which to describe relativistic physics.
Einstein’s field equations aren’t always possible to solve explicitly; in many cases only approximate solutions can be derived. This is a major area of research for modern physics and cosmology, since solutions to Einstein’s field equations lead to knowledge about the structure of the universe (is it expanding or contracting?), its origins in the Big Bang, and its contents, such as black holes and so-called dark matter. Modern computers make it possible to provide approximate solutions to Einstein’s Field Equations. Check out this latest work from Chinese and US researchers on possible solutions and modifications to Einstein’s Field Equations.




Leave a Reply