This article is the following of my article on game theory. We’ll go further in major concepts and examples of game theory. In particular, we will introduce evolutionary stable strategies, Stackelberg games, extensive form games, mechanism design, bayesian games and mean field games.
Hawks and Doves
Game theory was conceived for human interaction modeling. But, as it turned out, it has also had a lot of impact in ecology. In particular, the application of game theory to biodiversity by John Maynard Smith in 1973 has introduced a very active field of research. The classical example of that is the hawk-dove game. It’s also known as the chicken game or snow-drift game.
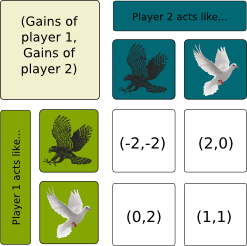
Contrary to what its name may suggest, the hawk-dove game is a game between two identical players. Each player can then act like a hawk, or like a dove, as they dispute some sharable ressource. If two doves meet, they gently share the ressource. If a hawk meets a dove, it gets the ressource as the dove flees. But if two hawks meet, they fight. In means, each will get half of the ressource, but they both get hurt so much that they wish they had not fight. This gives us the following payment matrix.
Now, let’s search for a Nash Equilibrium…
Indeed. I trust you for your ability now to do the reasoning to prove it.
That’s because I haven’t made it yet! Imagine now that we have a large population of a same species. As they walk (or fly) around, two of them sometimes meet. We assume that, in this large population, any animal either acts like a hawk or like a dove. The biologist’s question is to find a realistic model which would predict how animals would behave. This has led to evolutionary game theory.
What evolutionary game theory says is that not all animals will act like hawks: If there are only a few doves left, hawks will kill each other so much that the ratio of doves in the population will increase. On the opposite, not all animals can be doves. If there are only a few hawks left, these hawks will develop more easily as they will often steal the doves’ ressources. In fact, the ratios of hawks and doves will converge to an equilibrium. This point of convergence is an Evolutionary Stable Strategy (I’m not dwelling on it, but there is an actual definition of it that I don’t mention here).
Yes. We can match the ratios of hawks and doves with a mixed strategy, where the probability of being of each action is equal to the ratio of each kind. Having done that, any Evolutionary Stable Strategy corresponds to a Nash Equilibrium. Read my article on evolutionary game theory for more details.
Leaders and Followers
Evolutionary games have the specificity of players reacting to the other players’ actions made so far. The extreme case corresponds to Stackelberg games, with a leader and a follower. The leader plays first. The follower then reacts to the leader’s action. The leader knows that the follower’s action will be based on his action. He has to take this into account.
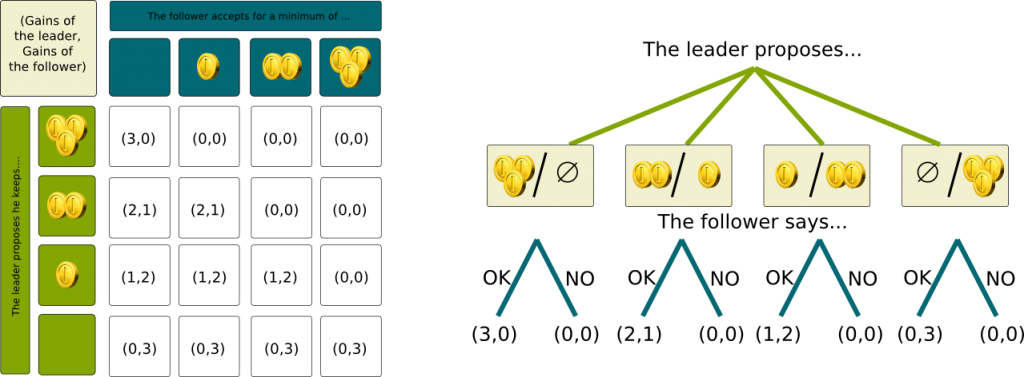
One example of that is the ultimatum game. Assume the leader and follower need to share 3 coins of $1. The leader proposes a way of sharing. The follower can then either accept or refuse the leader’s splitting proposal. In the case of the refusal, players fight and both win nothing.
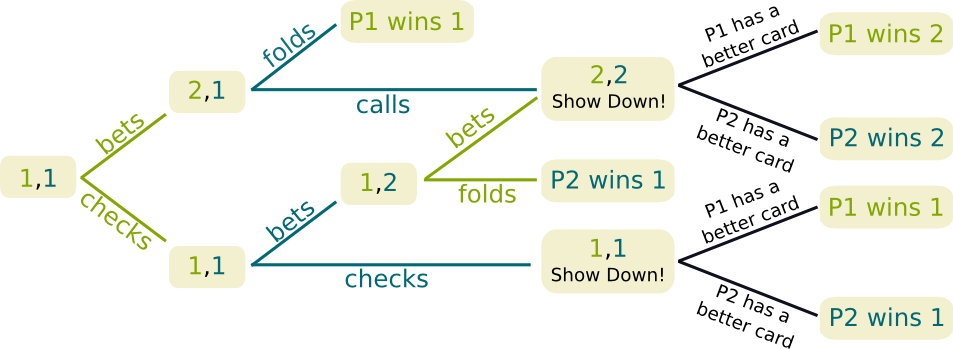
Well, you have to notice that the action of the follower depends on the leader’s action. Since the leader has 4 possible actions and since the follower has 2 possible actions for each of the leader’s actions, the follower has $2^4=16$ possible actions. However, we can reduce this number by only considering threshold-strategies, that is, actions which can be stated as: “I will accept if and only if the leader is proposing to yield at least $n$ coins”, where $n$ is either 0, 1, 2 or 3. This gives us the payment matrix displayed below, on the left. The payment matrix form known as the normal form.
However, the usual way of representing such games is rather through a decision tree. The first branches correspond to the leader’s decision, while the others, leading to the final result, stand for the follower’s decision, as displayed on the right of the figure below. This is known as the extensive form. Notice that this other representation is better, as it considers all possible actions of the follower, who can have weird strategies such as accepting if he is offered 1 or 3 but refusing if his is offered 2 coins.
As you can see on the payment matrix, the Nash Equilibria are the cases of the top-left to bottom-right diagonal. For instance, let us consider the third case where the gains are (1,2). As the leader chooses the line, he cannot do better. And as the follower chooses the column, he too cannot do better. Also, the top-right case is also a Nash Equilibrium.
You are right. By playing first, the leader can actually reduce the set of Nash Equilibria which can occur. A more restrictive concept than Nash Equilibrium has been introduced to better model the players’ behaviors. It’s called perfect Nash Equilibrium.
Let’s consider the extensive form of the game, that is, the tree. We have different positions of the game, namely, before or after the leader’s action. A strategy for a player is a matching between positions for which it’s his turn to play and decisions at those positions. Now, each position of the game induces a subgame, which begins at this point, reducing the set of actions. A perfect Nash Equilibrium is a strategy profile such that it’s a Nash Equilibrium for every subgame.
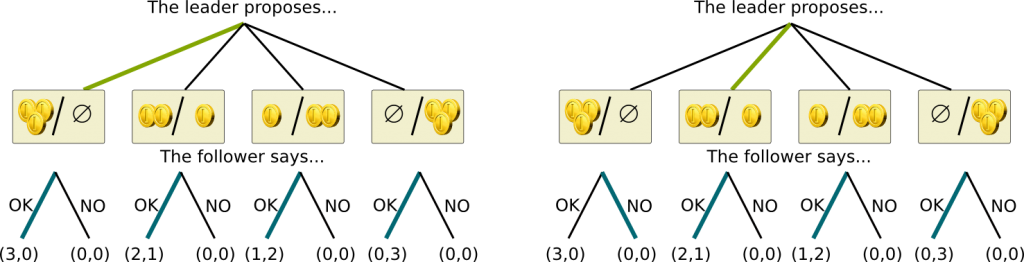
OK, let’s see an example. Let’s consider the strategy profile corresponding to the third case of the diagonal, where the outcome is (1,2). The strategy of the leader is to propose (1,2), while the strategy of the follower is to accept if and only if he is given at least 2. Let’s now have a look at the extensive form game to observe whether this strategy profile is a perfect Nash Equilibrium. In the position where the leader has proposed (2,1), the strategy profile says that the follower should refuse. Yet, this position induces a subgame where the follower should accept, yielding him a gain of a coin rather than nothing. Thus, although this strategy profile is a Nash Equilibrium, it is not a perfect Nash Equilibrium.
Well, there are two perfect Nash Equilibria in pure strategy, namely (2,1) and (3,0). They correspond to the strategy profiles shown below, where bolded colored lines stand for the strategies played.
I’ll let you check that in both cases and at every position of the game, the strategies form Nash Equilibria.
Yes! Let’s talk more generally about extensive form games.
Extensive Form Games
The most famous example of extensive form games is Chess. In chess, players react sequentially to each other until one checkmates the other. You could try to draw the extensive form tree representation of the game. However, the number of possible actions at each position of the game is large, and the number of possible positions is simply enormous.
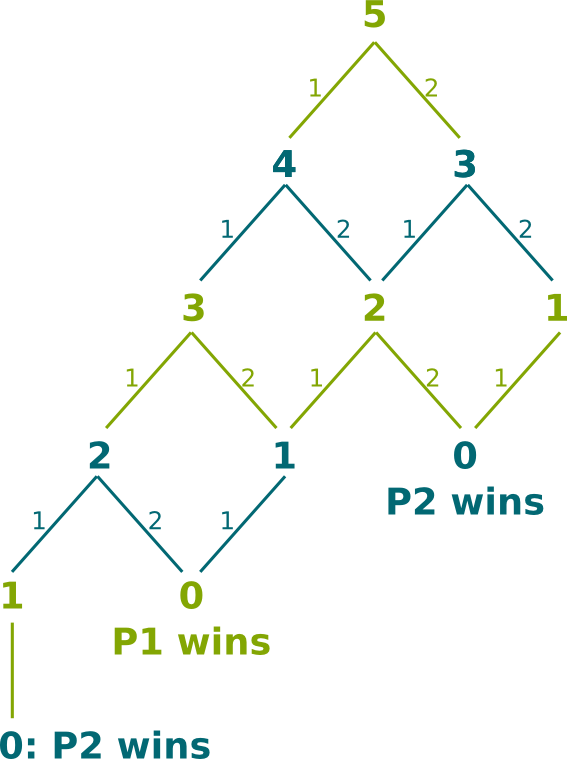
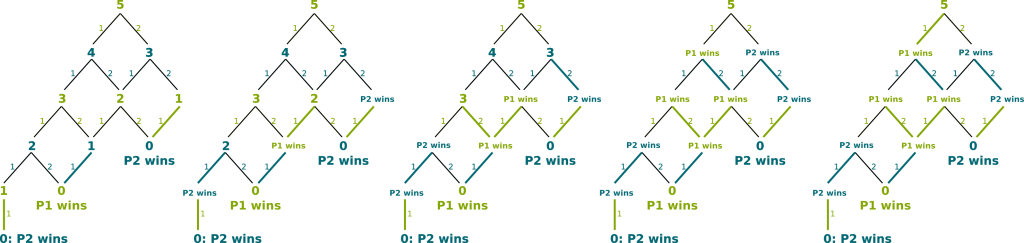
Instead of studying the complicated game of Chess, let’s consider another example. Consider a game between players in which there are 5 sticks. Then, players play sequentially. At each stage, the player whose turn it is can either take 1 or 2 sticks away. The one who takes the last stick is the loser. Player 1 plays first. On the right is the extensive form representation of the game, where positions are defined by the number of sticks left and whose turn to play it is. The green represents player 1, while the blue stands for player 2. On lines are displayed the number of sticks taken away by each player.
For simple extensive form games such as the one we are studying, it’s relatively easy to determine perfect Nash Equilibria. The idea is to study the most simple subgames first and find the Nash Equilibria of these simple subgames. Then, based on the Nash Equilibria of the simple subgames, we can deduce by induction the Nash Equilibria of the subgames which contain solved subgames. Eventually, we’ll obtain perfect Nash Equilibria.
Let’s see on the example. The most simple subgames are the games for which there is no choice for the players. Those are the bolded lines of the left figure. We deduce the result of the perfect Nash Equilibrium of those simple subgames. This gives the second graph. We can then use these results to solve subgames for which all lines lead to already solved subgames. Indeed, the player whose turn it is will make the decision that leads to a subgame he wins, if this exists. Otherwise, he can make any decision, as they all lead to his lost. This is how we obtain the third, fourth and fifth graphs.
Eventually, this method enables us to find a perfect Nash Equilibrium of the game. As you can see, at the perfect Nash Equilibrium, the winner is player 1. This method is actually a specific case of dynamic programming. Dynamic programming is a state-of-the-art optimization algorithm for problems with a certain structure such as the one of extensive games. There is a lot to say about it, and you are more than welcome to write an article on the topic.
In Chess, the number of positions of the game is astronomical. It’s estimated at 1045. If a computer checked billions of billions of positions in a second, then we’d still need billions of billions of billions… well I’m not going to say how many years we’d need but it’s way more than the age of the Universe. Computers can’t apply exact dynamic programming. They actually use an approximate dynamic programming. Once again, there is a lot to say about algorithms to play Chess… If you can, please write about them!
Indeed. More generally, this algorithm shows that any finite extensive form game has a perfect Nash Equilibrium in pure strategies. In fact, applied to Chess, this implies that either the first player or the second player has a winning strategy… Unless they both have strategies which guarantee a tie.
Mechanism Design
Mechanism design is a particular form of extensive games, where a leader, called principal, regulator or mechanism designer acts first. His action induces a game that is to be played by several other players.
The most classical example of mechanism design is the auction designing problem. In auctions, the principal is the seller. He has a good to sell. He wants to sell it at the highest possible price. There is a set of buyers in front of him, who all have their own secret valuation of the good. The seller’s mechanism design problem is to define an auction system. One classical way of doing that is the English auction, in which buyers bid prices. The highest bidder becomes the buyer, and the selling price is his bids. One problem with this mechanism though is that players have incentives to bid undervaluations of the good to get it at the lowest possible price. This can lead to long argument with slight increase of the highest bidding price.
There are plenty of other applications of mechanism design, including market regulation, voting schemes, school or university assignment, political decisions or sports competition organization. For instance, in the 2012 Olympic Games in London, 8 Asian badminton female players have been disqualified for throwing games. This was opposed to olympic values. Yet, the design of the mechanism of the competition gave incentives to already qualified players in the round-robin not to try their best to win their games. The mechanism was in fact incompatible with the olympic values. It’d be much better to have olympic-value-compatible rules of olympic competition.
Mechanism design often deals with truthfulness of players. For instance, we’d like to design an auction in which players have incentives to reveal their valuation of the good. One great result of mechanism design is the revelation principle. It states that, for any mechanism played at an equilibrium, there exists a payment-equivalent mechanism in which players have incentives to be truthful. Applied to auctions, this leads to the Vickrey auction, also known as the second-highest bidder auction. In the Vickrey auction, the good goes to the highest bidder, but the price is defined by the second-highest bid. This auction gives incentives to players to be truthful. In fact, no matter what others do, each player has incentive to be truthful: Truthfulness is a dominant strategy.
Mechanism design is a very interesting field because it has plenty of applications. It’s a relatively recent theory. Indeed, its main founders, namely Roger Myerson, Eric Maskin and Leonid Hurwicz, received a Nobel prize in economy in 2007. Learn more with my complete article on mechanism design.
Incomplete Information
A great difficulty of mechanism design is the fact that players have secret valuations, ambitions or constraints. This private information is called the type. In fact, a mechanism induces a game between players who have incomplete information about the others’ types. This sort of game is called Bayesian game, after the name of the English mathematician Thomas Bayes, who is known for his contributions to probability theory.
The knowledge about the the types of the players is modeled by a probability over its possible types. This probability is called the belief. For instance, assume that Phil and Andrew are playing some card games. In card games, the private information is the cards in hands. Then, Phil has some beliefs on Andrew’s type, including depending on his own type. Indeed, if Phil has the ace of spade in his hand, then he knows that Andrew doesn’t have it. A third player may have another belief on Andrew’s type.
Indeed. Poker is a very classical example of Bayesian games. In poker just like in any Bayesian games, the others’ types matter just as much as your own type. Sometimes even more than your own type…
Yes there is, except we call it Bayesian-Nash Equilibrium. A Bayesian-Nash Equilibrium is still a strategy profile such that each player’s strategy at the Equilibrium is a best-response to the other players’ strategies at the Equilibrium.
Well, that’s where the difference is with classical games. A strategy is a mapping of a type with an action, just like in extensive form game, a strategy actually is a mapping of a position with an action. Given all the players’ strategies, we can evaluate the expectations of the gains of players. A best-response for Phil against Andrew’s strategies is then a strategy maximizing Phil’s expected gain, assuming that Andrew will play his strategy, and given Phil’s belief on Andrew’s types.
Let’s take the example of Kuhn Poker, invented in 1950. This simplified version of Poker is a two-player nil-sum extensive form game with incomplete information. At the beginning each player is dealt one of three cards. The cards are a Jack, a Queen and a King. The following tree displays the game can be played. The pair of numbers at each position represent the total bets of the two players. Once again, player one’s possible actions are the green lines, while player two’s are the blue lines.
I have no idea… The incomplete information makes the game much more complicated to study. But there may not be any Bayesian-Nash Equilibrium in pure strategies. In fact, things become even more complicated if you consider the fact that at each position of the game, players can deduce from the other player’s actions made so far a more accurate belief on the other player’s type. This is actually where the Bayes’ theorem can be applied to update the beliefs on a player’s type after each action of this player. Yet, especially in poker, it’d be bad for you to let the other player improve his belief on your type. Thus, mixed strategies are better. This means that from times to times, you should bluff to avoid others knowing your own type.
Indeed. In my PhD, I am working on ways to determine Bayesian-Nash Equilibria in pure strategies for normal form games, which is already very difficult. Determining Bayesian-Nash Equilibria in mixed strategies for extensive form games seems way more difficult. It’s a field of research with plenty of open problems. To go further, read my article on the topic.
Mean-Field Games
The future of game theory may also lie in another sort of games…
Most methods to solve games mainly focus on 2-player games. Things get awfully more complicated once you consider 3, 4 or, god forbid!, $n$ players. Yet, most of the games we actually play in real life concern a great number of players. One example is the unscrupulous diner’s dilemma. Imagine you go out for dinner with friends, and before the meal, you decide to split the bill evenly. Then, you can decide to have a cheap or an expensive meal. You may think that the expensive meal is not worth it, but if only you choose the expensive meal, you’ll get to eat well while still not overpaying, since the bill will be split.
Variants of this problem when the number of player is even higher are the public goods game and the free-rider problem. These two games are similar. Let’s illustrate the free-rider problem. In a city, you can either pay when using the public transport or not. The more people pay, the better the public transport. However, each individual can benefit of the good public transport and still decide not to pay for it.
Yes we can. This is the crucial assumption of mean-field games. In this setting, one individual’s action has no effect on the global outcome. This hypothesis enables plenty of simplifications, including assumption of a continuum of players which enables derivation! In fact, the ideas of mean-field games mainly come from statistical mechanics.
Let’s sum up
I hope this overview has enabled you to have a glance at what is being done and what can still be done in game theory. More and more concepts have been developed as more and more problems have been thought in terms of games.


Leave a Reply