The four symbols of the formula $P=NP$ represent the best-known fundamental open problem in computer science and mathematics. First raised by the puzzling Austrian-American mathematician Kurt Gödel, it’s registered among the 7 Millenium Prize problems, and it’s probably the most important open theoretical problem we currently face, because of its many fallouts. In this article, we’ll present P, then NP and then we’ll discuss the open problem. This article deals with a very theoretical problem and I’ll try to make it simple… but it will still be a little bit technical.
Humm… I get your point! So, before getting technical, here’s a simplified definition of this crucial problem, which I presented in my talk More Hiking in Modern Math World:
P
Let’s start by understanding the symbols of the formula. Let’s start with $P$. It represents the set of decision problems that can be solved by a deterministic Turing machine with a polynomial time complexity in the worst case.
Waw, that’s a lot of questions! One at the time, please!
OK! A decision problem is a question that takes into account an input and whose answer is yes or no. For instance, the problem “Are the elements of the array all different?” is a decision problem that takes into account the array as input, and whose answer is either yes or no. Simple, right?
Before giving you the definition, let’s remark two facts. First, note that deterministic Turing machines are commonly simply called Turing machines. Second, Turing machines correspond to the algorithms we usually define (with tests “if”, loops “while” and “for” and recursions). Although not all algorithms correspond to a Turing machine (and we’ll mention some of those later), most of the algorithms we use or write on computers match the definition of Turing machines.
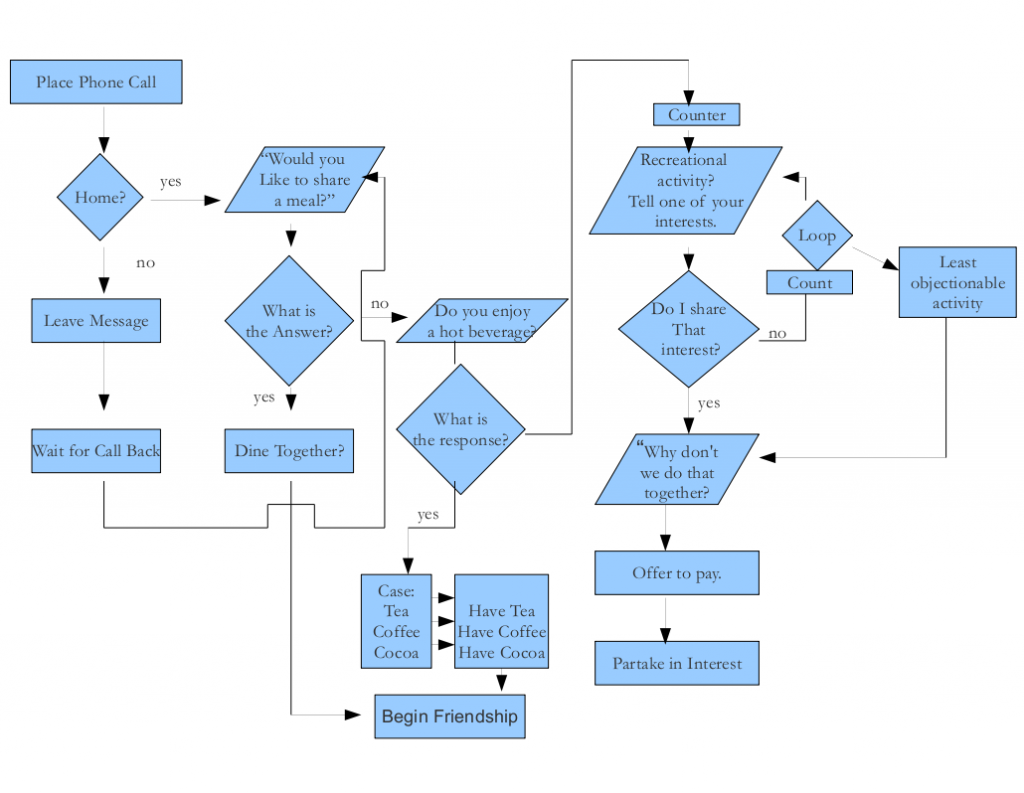
A Turing machine can be understood as a set of possible states, with transitions between states. At each step of the algorithm, depending on the current state and on the input that’s being read by the machine, a transition towards the next state is taken. Each transition corresponds to a basic operation. For instance, Sheldon’s friendship algorithm (see this video) can be drawn as the following Turing machine, where states are the blue areas and transitions are the arrows:
There are certain specific states. One is the initial state. In Sheldon’s algorithm, the initial state is the one on the top left called “Place Phone Call”. Also, there are states known as final states or accepting states. At theses states, the algorithm finishes. The result of the algorithm is defined by the final state it will eventually reach. In Sheldon’s algorithm, this refers to states “Begin Frienship” and “Partake in Interest”. In decision problems, some states may refer to the answer “true”, others to the answer “false”.
No. Look at Sheldon’s friendship algorithm for instance. If it didn’t have a loop count, it might stay in this loop indefinitely. In fact, knowing whether an algorithm will reach a final state is a difficult problem. Indeed, in the late 1930s, Alan Turing, founder of modern computer science, has proved that there does not exist any Turing machine that, given a Turing machine and an input, can determine if the Turing machine will finish with the input. Equivalently, we say that determining whether any Turing machine will halt with any input is undecidable. This problem is known as the halting problem and is a particularly case of Rice’s theorem. This theorem says that non-trivial problems are undecidable. But this is getting complicated and I’m not going to dwell on that.
Computers can be modeled by Turing machines. Indeed, each state of the entire memory of the computer can be modeled by a state in the Turing machine. Now, at each step of an algorithm run on a computer, the memory and the input are read, and, based on the given instruction, a decision to overwrite the memory is taken. This leads to a new state of the memory. Thus, the decision to overwrite corresponds to a transition.
Here is a little more on Turing machine. As Alan Turing proved it, there exists a Turing machine, called universal Turing machine, such that, any other Turing machine can be simulated by the universal Turing machine, by writing the instructions on the inputs. For computers, this corresponds to saying that programming languages like C++ or Java are universal Turing machines. You can write instructions, add inputs and give it to those languages to have any algorithm running.
The important fact is that computers can be understood as Turing machines. Thus, algorithms we usually write fall into the definition of P.
Well, for that I first need to talk about the size of the input and the time it takes for an algorithm to finish…
Well, yes, the size of the input is often measured in bytes. But in many case, we prefer to describe the size of the input with a number that is proportional to the size in bytes. For instance, in the case of the array, the size of the input can be considered as the number of elements of the array. Either representation is equivalent to the definitions we’ll see.
Well, the problem with measuring the time in seconds is that the time an algorithm will take to finish strongly depend on the power of your processor. And that’s not all, as computers now muli-task everything, if you run an algorithm with the same input twice on the same computer, it will probably not take the same number of seconds to finish. That’s why, when it’s possible, we prefer to measure is the number of basic operations (tests, additions…) done by the computer. This other time is almost proportional to the actual time in seconds, and is equivalent for the definitions we’ll see.
Yes! A Turing machine has a polynomial time complexity if there exists a polynomial $P$ such that for any input of size $n$, the time it takes for the Turing machine to halt is less than $P(n)$. In this case, we’ll know for sure that the algorithm will finish in a reasonable amount of time for any input. This corresponds to saying that even in the worst case, the complexity time is polynomial in the size of the input.
Some algorithms are known to have a different complexity in average and in the worst case. An algorithm has a polynomial time complexity in average if the means over input of size $n$ of the time the Turing machine takes to halt is less than $P(n)$. However, we need to be careful with such a definition as it’s implied that there is a uniform distribution over input of size $n$. Yet, such a uniform distribution may not model well the reality, or needs to be defined. For instance, the quick sort (see my article on divide and conquer) is known to have a good complexity in average but performs very poorly on already sorted lists, which there are not a lot of if we consider a uniform distribution over mixings of the lists. Yet, in practice, we often work on sorted lists.
I guess you have now all the information to understand what a decision problem that can be solved by a Turing machine with a polynomial time complexity in the worst case is.
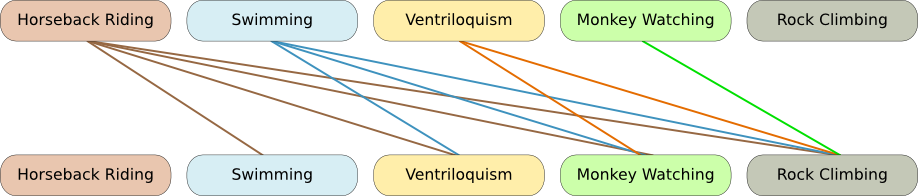
Sure! Instead of asking the other person to make suggestions one at the time, Sheldon could ask the other person to give a list of suggestions. However, Sheldon is a bit paranoiac, so he’ll make sure that the other person doesn’t mess with him. For instance, he may want to make sure that all suggestions are different from each other.
The problem of testing whether elements of a list are all different is in P. First, it’s a decision problem. Then, let’s consider the following algorithm. We’ll consider every pair of elements of the list. If the two elements of every pair are different from each other, then the answer will be “true”.
Well, the usual way is to give an order to the elements of the lists. Then, we will consider the matchings of each element with every of its followers in the lists. Here is a graphical representation of that, where each line corresponds to a pairing.
This algorithm does answer the question. In addition, if there are $n$ elements in the list, since there are $n(n-1)/2$ pairs of the list, we’ll have to do at most $n(n-1)/2$ iterations, with one basic operation per iteration (the test of whether the former differ from the latter). Thus, the number of operation is less than $P(n) = n(n-1)/2+1$. Thus, the algorithm is polynomial. Thus, this decision problem can be solved by a Turing machine in polynomial time in the worst case: It’s in P.
NP
Let’s now talk about the two last symbols: NP.
No! Although the “N” does stand for “Non” and the “P” for “Polynomial”, “NP” stands for Non-deterministic Polynomial. It’s the set of decision problems that, if the answer is true, can be solved with a non-deterministic Turing machine in polynomial time in the worst case.
A non-deterministic Turing machines is pretty much like a deterministic Turing machine, but has a few differences. Mainly, it enables, given a state and an input, transitions towards several states or none at all. If there is a path using these transitions from the initial state towards a final state, then the machine returns “true”. Because of that, non-deterministic Turing machines are very different from Turing machine. The answer is not read on the final state reached as there may be several final states that can be reached. If an answer is found, it’s necessarily “true”.
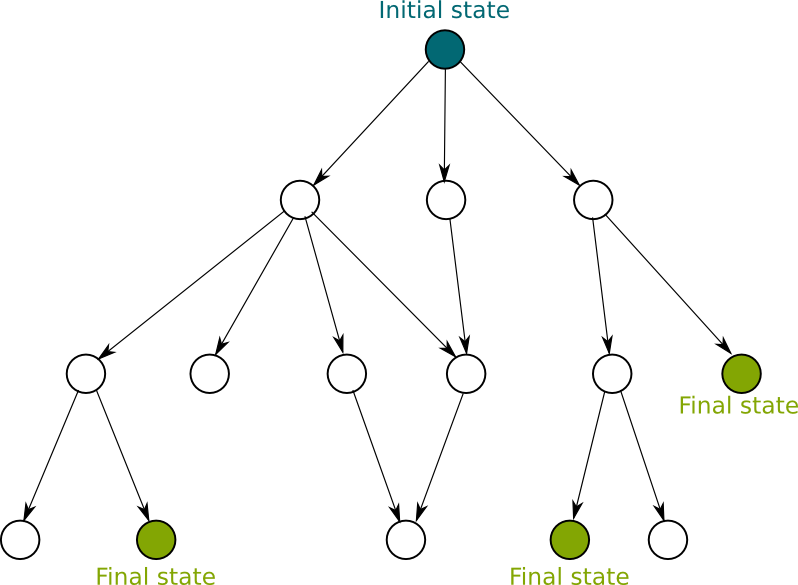
As opposed to deterministic Turing machines that can be described as paths from the initial state to a final state via intermediate states using transitions, a non-deterministic Turing machine cannot be drawn as a path. It needs to be consider as an arborescence, that is a structure in which each state has zero, one or several “child” states (even though it’s not exactly an arborescence in the sense of graph theory since there can be several paths from the root to a state, or since there can be cycles). Equivalently, the answer given by the deterministic Turing machine is “true” if there exists a final state in the arborescence. The following figure is a representation of the arborescence of a non-deterministic Turing machine.
As you can see, states can have zero, one or several transitions. In this example, since there exists final states in the arborescence, the answer is “true”.
Non-deterministic machines can be understood as machines that do each of the possible transitions simultaneously (by, for instance, branching it to another similar machine) and finishes as soon as one of the path of transitions finds a final state. They can also be understood as lucky guessers that will always choose the right transition, to reach as quickly as possible a final state.
For inputs for which the answer is “true”, we can define the time complexity as the number of transitions of the shortest path towards a final state. Similarly to P, we can define the set of problems such that there exists an non-deterministic Turing machine that correctly answers true with a time complexity that’s bounded by a polynomial function of the size of the input. Such problems are called non-deterministic polynomial, that is they are in NP.
Fortunately, there exists interesting links between non-deterministic and deterministic Turing machines that can help us deal with NP problems. For one thing, any problem that can be solved with non-deterministic Turing machines can be solved with a Turing machine. In addition, any problem in P is also in NP.
But that’s not all! The most important result is the following. A problem is NP if and only if, for any input, there exists a finite (but potentially enormous) set of decision subproblems that are in P, such that the answer of the problem is true whenever the answers of all decision subproblems are true too.
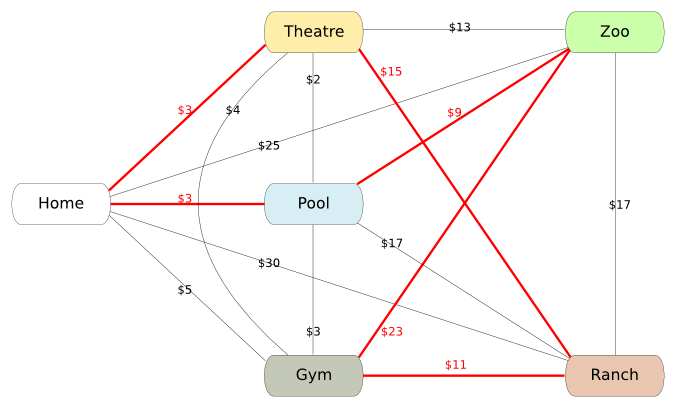
Suppose Sheldon does not know what the proposed activities are. He’ll need to go to each of the places to see what they are and how they work. However he only has $50 for taxis. His problem is finding out whether he’ll be able to visit all those places.
The previous figure displays the different places and the cost of taxis from each place to another. The red lines are a possible travel for Sheldon. However, the red travel costs 3+15+11+23+9+3=64 dollars. Since Sheldon only has $50, it’s a travel he can’t undertake.
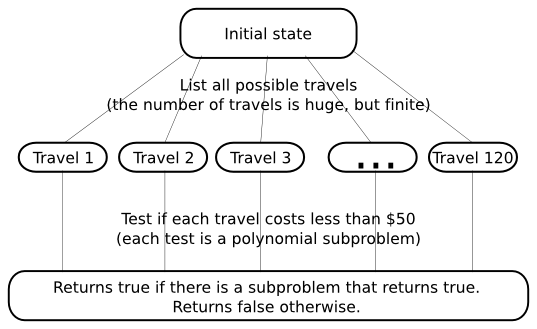
In order to know if he can visit all the places with $50 only, he can test all travels that go through every place. As there is a finite number of travels that go through every place, and as testing if a travel is feasible with $50 can be done very quickly (by adding all taxi costs and comparing the total to $50), this problem falls into the equivalent definition of NP problems. It is therefore NP. Not that this algorithm that simultaneously tries all travels is not really an algorithm done by a deterministic Turing machine.
Sheldon’s problem is actually an example of the traveling salesman decision problem. This problem consists more generally of deciding whether there exists a path that starts and ends at home, and goes through all intermediate points so that the total cost of travel is less than some value. The input is the set of intermediate points and the costs of taxis between two points.
Notice that we could modify the algorithm by sequentially testing all travels. The algorithm we’d obtain is a deterministic Turing machine. But it is not in P. As a matter of fact, if there are $n$ places to visit, then there are $n \times (n-1) \times … \times1 = n!$ ways of travelling via every place. In our example with only 5 places to visit, the algorithm requires 120 tests! In fact, $n!$ cannot be up-bounded by any polynomial. This proves that the algorithm is not polynomial.
Also note that in plenty of articles, by misuse of language, non-decision problems are sometimes categorized into P problems (or other classes of decision problems) that are supposed to be decision problems only. This usually simply means that solving the problems can be done in polynomial time (or in the same time as decision problems of the class mentioned). However, be aware that concerning NP problems, many articles simply make mistakes and write for instance that the traveling salesman problem is NP. Because of the specific definition of NP, only decision problems can really be considered NP!
Wondering if any problem in NP is also in P, that is if any NP problem can be solved in polynomial time with a deterministic Turing machine. As I said, it’s a major open problem… and I’m not going to be the one with the answer! But if you want to give it a shot, you should know about concepts like NP-hard or NP-complete.
NP-hard, NP-complete
In complexity theory, a problem A is said harder than a problem B, if B can be solved using a polynomial number of basic operations and by using a polynomial number of times a solution to A. Equivalently, we say that A is harder than B, if, when we assume that there exists a basic operation that solves A, B can be solved in polynomial time. In this second equivalent definition, the basic operation that solves A is called an oracle for A.
Let us show that the problem of finding the smallest cost of travel (call it problem A) is just as hard as the problem of knowing if there is a possible travel with a certain amount of money (call it problem B and note that it’s Sheldon’s problem we described), when the taxi costs are all integer (that would be true without this assumption, but we’ll add it to make things simple). First if we can find A in one basic operation, solving B can simply be done by comparing the amount of money with the smallest cost of travel. Thus, A is harder than B.
Let us now show that B is harder than A. We know that the smallest cost of travel is between 0 and the sum of costs of taxis between 2 points. So we can simply use a dichotomic search to find the smallest cost of travel. At each step, we know that the smallest cost is between two values. We consider the means of the two values. We apply the oracle of B to know if the tested value is higher or lower than the smallest cost is higher or lower than the tested value. We then adapt our interval where we know the smallest cost is. By applying this dichotomic search, the number of times we used the oracle of B is smaller than the logarithm of the sum of costs of taxis between 2 points, which is about the number of digits necessary to write the costs of taxis. As a result, the number of uses of B is polynomial in the size of the input. Therefore, B is harder than A. As we had already showed that A was harder than B, we can now say that both problems are as hard as each other.
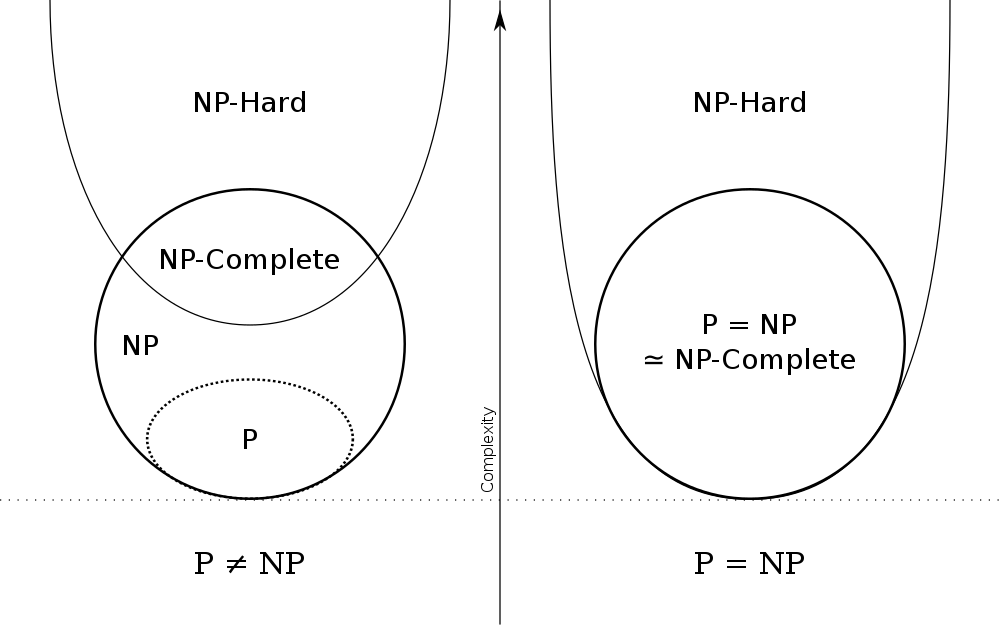
Yes! We call NP-hard the set of problems (not necessarily decision problems) that are harder than any NP problem. Weirdly enough, NP-hard problems are not necessarily NP. There are plenty of NP-hard problems, and these problems are definitely… hard.
But what’s very interesting is actually the intersection of the set of NP-hard problems and the set of NP problems. This set is called NP-complete.
First, because if you can find a polynomial algorithm to solve a NP-complete problem, then you’ll have proved that $P=NP$! Obviously, this is actually true for any NP-hard problem, because of the definition of “harder” we gave earlier.
But mainly, because we know a lot of NP-complete problems, so you can pick the one you want to try to solve. Among them, let’s mention the boolean satisfiability problem, the knapsack decision problem, the traveling salesman decision problem, the graph coloring decision problem… All these problems are extremely interesting and they deserve their own articles. Please write about them if you can!
Well, if $P=NP$, then a lot of the research in optimization would be pointless. Many problems scientists now face would be instantly solved, such as DNA reconstitution, Nash equilibrium computation, vehicle routing… But more importantly, several nowadays’ systems, especially in cryptography, are built considering that $P \neq NP$, that is that no one will be able to crack the system in less than a few million years. For instance, private communication through the web including with your bank use cryptic protocols. One of them is the RSA system, in which each institution has a private key and gives away a public key. You can talk to the institution by encoding your message with the public key, but no one except the institution will be able to decode your message as the private key is required for that. And the institution believes that no one will be able to guess the private key with the public key… which could actually be done, but it may take a few million years. If $P=NP$, an algorithm may be found to solve it in matters of days or less! I’ll let you imagine the consequences… There would be solutions in the long run, as explained by Scott’s article on quantum cryptography.
Most scientists actually tend to believe that $P \neq NP$, which means that NP-hard problems are intrinsically difficult problems. And it will be safe to make systems that assume that a NP-hard problem can’t be solved in reasonable time. Anyways, here is a graph of what would be the consequences for the relationships between P, NP, NP-complete and NP-hard.
Let’s sum up
The problem $P=NP$ is a very difficult fundamental open problem with plenty of major practical implications. That’s why it’s probably the current major problem. Moreover, there are plenty of interpretations of $P=NP$. Some of them actually consider that the way we understand the world is globally understood, including the concept of the creativity, would be greatly affected. Here’s a wonderful video by Hackerdashery:
Note that it’s not the only fundamental open problem in computational complexity. In particular, you can read my article on divide and conquer to learn about $P=NC$, that deals with the possibility of parallelization of algorithms. Other problems include $NP=co-NP$, where $co-NP$ is the set of decision problems solvable by a non-deterministic Turing machine in polynomial time when the answer is “false”. There is also $P=BPP$ or $NP=BQP$, where $BPP$ refers to probabilistic algorithms and $BQP$ to probabilistic quantum algorithms. You can learn about these two in my article on probabilistic algorithms.
No! I’m no expert in this problem. But many scientists tend to believe that $P \neq NP$, although their main argument is that, if P=NP, then one of them would have found a polynomial algorithm to solve one of the NP-complete algorithms… Or maybe it’s just an excuse to justify that we just don’t know the answer… Even more troublingly, some scientists suggest that the problem might be undecidable! This would mean that there is no proof that $P=NP$ nor that $P\neq NP$. A cause of that would be that mathematics is just not developed enough to address this question (and, maybe, could never be developed enough!). You can learn more on undecidability in my article on self-reference.
Let’s note though that there are problems which have been proved to be strictly harder than P problems. Also remark that, even if $P \neq NP$, there may be algorithms that can solve NP-hard problems in polynomial time in average.

Leave a Reply