How can scientists define theories describing the immensity of the Universe? I’d say that the key component is symmetries. In fact, the mere concept of science requires the consideration of a symmetry: If we do the same experiments in different times or places with the same conditions, then results should match. The symmetry of space and time lies in this simple sentence, as explained by Henry Reich on MinutePhysics:
Particle physics takes this concept of symmetry even further: It consider that particles are symmetric in some sense. But reality isn’t the only field where the virtues of symmetries highly contribute. Art is full of them. Egypt’s ancient pyramids are geometrical wonders, musics follow remarkable patterns, Jackson Pollock’s paintings display fractal symmetries and even movies and series apply symmetry to actors’ lines, like in this extract from friends. It’s also a major concepts in our society, which tries to consider its inhabitants symmetrically, to ensure fairness.
Symmetry often lies behind beauty. As a mathematician, I am fascinated by the beauty of symmetries.
Symmetries in Geometry
I know. Yet, symmetries are not restricted to geometry. But let’s start with these symmetries. After all, they are the first ones in the History of mathematics.
Reflection
In particular, the first one that would come to most people’s mind is the symmetry induced by a mirror. This is known as the reflection symmetry, as displayed in the following picture, where the mirror is the Okarito lagoon on the West Coast of New Zealand’s South Island.
This symmetry is actually a matching of any element of the picture with an image. The image of an element is obtained by turning the element around the axis of symmetry. The following figure shows how the image of a star-shaped element is obtained:
Reflection symmetry has plenty of nice properties, but I won’t get into this now, as I want to talk more globally about all symmetries. But if you can, please write an article on the topic.
Translation
I actually find the reflection symmetry rather complicated, at least compared to translations.
Translations consist in moving elements. It’s a symmetry that appears a lot when several products are made out of the same models and put near each other, like these statues of Angkor:
Notice that all elements of the picture must have the same motion. This motion is characterized by a direction and distance. These are captured by the concept of a vector. Vectors are a fundamental concept of mathematics. If you can, please write about them.
Point Reflection
Now, the first symmetry we’ve discussed was a reflection symmetry with respect to an axis. Following this idea, we can consider reflection symmetries with respect to a point, called… point reflection.
Point reflection is a symmetry that is used by eyes and cameras to capture an image. Let’s see how it works with this picture taken inside the amazing Cloud Gate of Chicago, also known as The Bean:
Notice that point reflection can also be obtained by turning upside down around the point of symmetry.
Great question, whose answer is: Sure, why not?
Rotation
If we stop before (or after) being upside down, then, we’ll be doing what’s known as a rotation. Rotations appear in circular motions, like the Earth around the Sun, but also on waves, where a central disturbance implies motions away from a central point, such as these chickens running away their mother:
Just like for point reflection, the central point here plays an important role. But the even more important variable is the angle of rotation. The central point and the angle define the rotation.
The four operations we have seen so far, that is, reflection, central reflection, translation and rotation, guarantee that the image of an element will have the exact same dimensions as the element. This property is known as isometry, which, derived from ancient greek, means same (iso) measure (metron). Figures which have a lot of isometries form beautiful tessellation. These can be found in mathematics and arts, but also in nature and constructions:
Isometries are largely studied in mathematics, as they can be defined for any metric space. This includes space with many more dimensions! In particular, in linear algebra, all isometries leaving the origin still are regrouped in the set of orthogonal matrices, which play a central role. If you can, please write about orthogonal matrices. Moreover, as explained by Scott, the study of isometries is essential to map-making.
Newton’s mechanics consider that space was isometric, when measured by different observers. Yet, this has been proven wrong by Einstein (see my article on his spacetime).
In fact, it is, in some sense, even thought it’s not isometric. These leads us to homotheties.
Homothety
Consider our first description of point reflection. If we didn’t stop until we arrived on the opposite of the point, we would have done a homothety. Simple, right? Now, this property is the key element of perspective, which was a great breakthrough in art during the European Renaissance. It’s how we observe elements translated into the background, such as in the case of the following picture of the Golden Gate Bridge:
The homethety is defined by the central point and a ratio. This ratio says by how much distances will be multiplied. It can even be negative, in which case we would carry on the motion into the opposite side of the central point. In fact, you may notice that a ratio of -1 makes the homethety equivalent to point reflection.
Not exactly. In special relativity, only one direction is contracted. This corresponds to a homothety according to an axis instead of a point (or, more accurately in Einstein’s theory, according to a plane). This gives us the following contraction:
The plane or axis, and the ratio define this specific homothety. To learn more, read my article on spacetime of special relativity.
Yes we can. And this yields some of the most beautiful wonders of mathematics: fractals. Fractals correspond to object which appear to remain similar once you zoom in. They occur in plenty of natural phenomena, and is applied in certain fields, such as virtual image creation. Here are some of these wonders:
To learn more, read Thomas’ article on fractals.
The list of symmetries we have described so far is not exhaustive. But they are the best-known and most visual symmetries. So let’s go further in their study!
Groups of Symmetries
Let’s focus on translations and rotations. In the following, whenever I refer to symmetries, I mean translations and rotations only. The reasonings would be similar, although a little more complicated, if you add other symmetries, but the fundamental concept of group would remain.
Before getting to the definition of what a group is, there are two major remarks which need to be made regarding translations and rotations we have defined.
First, these symmetries are bijective and the inverse of a symmetry is a symmetry.
Bijectivity means that symmetries correspond to one-to-one matching between points of the initial image and points of the obtained image. More precisely, given any symmetry, every point has a unique image through this symmetry, but, also and more importantly, every point is the image of a unique other point, called fiber.
Symmetries can therefore be inverted. The inversion of a symmetry correspond to a transformation. Well, the second part of the remark is that this inverting transformation, called the inverse, is also a symmetry. Indeed, inverting a translation is equivalent to a translation towards the opposite direction. Similarly, inverting a rotation is equivalent to a rotation of the opposite angle with the same center.
The composition of symmetries is a symmetry.
A composition of several symmetries is the operation of successively applying each of the symmetries. For instance, the composition of two translations corresponds to applying the second translation, and then the first translation. Now, it can be shown that composing any 2 symmetries yield a symmetry. If you compose 2 translations, you get a translation whose motion is the sum of the motions of the 2 translations. You can see this in the following figure:
Yes! If you composed two rotations, you’d obtain a rotation whose angle is the sum of the angles of the two rotations, unless the sum of the angles is nil, in which case you’d obtain a translation. Determining the center point or the translation motion is more complicated though and I’m not going to describe how it’s obtained. Similarly, composing a translation and a rotation makes a rotation of the angle of rotation, but whose center is complicated to describe. But you should try to find these on your own. That’s an interesting exercise!
Composing more symmetries is equivalent to composing all of them but two successive ones, with the composition of these two symmetries. For instance, if you need to compose a first rotation, a translation and a second rotation, then it’s equivalent to composing the first rotation with the composition of the translation and the second rotation. Yet, the composition of the translation and the second rotation is a composition of 2 symmetries and is therefore a symmetry. Thus, composing the first rotation with it corresponds to the composition of 2 symmetries two and is therefore also a symmetry.
Great. Let’s recapitulate. If we only consider rotations and translations as symmetries, then symmetries are invertible and their inverses are symmetries. What’s more, the composition of two symmetries is a symmetry. Those two properties are what defines a group. That’s why we talk about the group of symmetries.
By identifying this structure of symmetries, we’re entering a fundamental and vast field of mathematics, called algebra. Algebra is the study of inner interactions of elements of a set. And being group is one of the most fundamental inner-interaction property a set can have.
Numbers are another example of group, as they can interact with each other by addition. Indeed, addition with any number is invertible, by then subtracting that same number. And, as you all know, adding two numbers does give a number.
Let’s have a closer look to the group of symmetries!
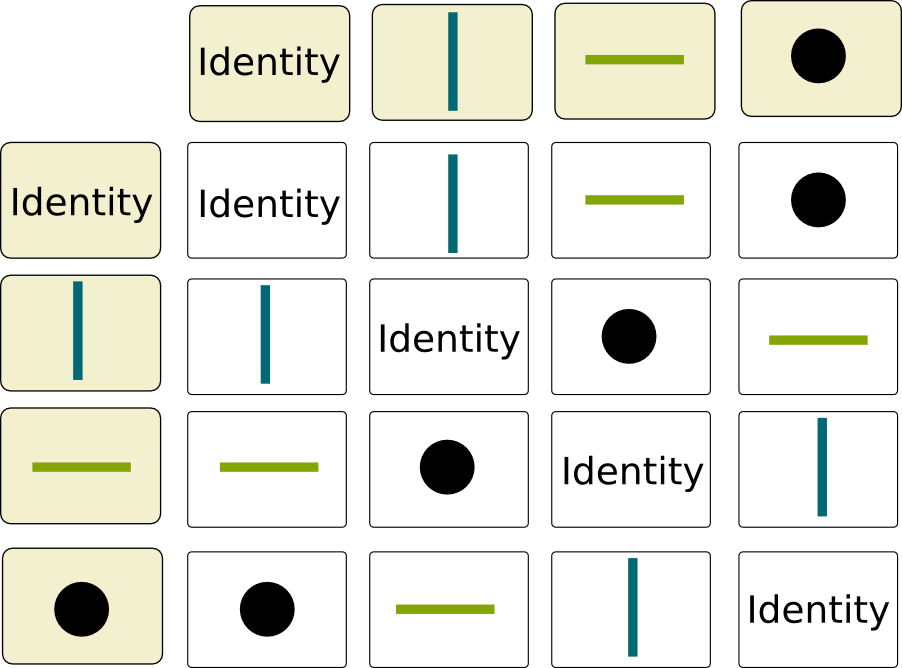
Let’s take a simpler group of symmetries. Historically, the concept of group theory comes from French mathematician Évariste Galois in the 1830s, by studying particular kinds of symmetries: the symmetries that leave a particular figure unchanged. Let’s do this, as we consider the Japanese Bridge of Hoi An in Vietnam, and its reflect on water:
As you can see on the figure, 4 symmetries leave the bridge untouched, namely the vertical axis reflection, the horizontal axis reflection, the point reflection and… the doing nothing symmetry, better known as the identity! Now, we can also draw the compositions of these 4 symmetries, which are summarized in the following table, pretty much like a multiplication table. Each entry says what we obtain when we compose the symmetry of the row with the symmetry of the column.
Now, if you take another figure, you’d get another table. Each of these table defines a group. Now, it’s interesting to notice some of the properties of these tables. For a start, the rows and columns corresponding to the Identity correspond to a copy of entries. More interestingly, each element appears exactly once on every row and column, kind of like in sudokus. This is due to the invertibility property of compositions. It makes the table a latin square. There is an interesting relationship between latin squares and groups, but I’m not going to dwell on it…
In the following video, British mathematician Marcus du Sautoy talks about other groups of symmetries, in a very nice way:
That’s very perspicace of you. Indeed, weirdly enough, symmetry is a widely-used concept. Yet, even mathematically, there is no accurate definition of it. One reason is that, as mathematics have progressed, more and more symmetries have been invented. This has led to the lack of its definition… until the larger concept of automorphisms unified all symmetries.
Morphisms
Indeed. It comes from greek words autos and morphe, which mean self and form.
Kind of. More mathematically, an automorphism is a particular sort of morphism.
It’s probably the most important concept of mathematics, or, at least, of category theory. Category theory is the study of structures of objects. But some of these objects can be very complicated. In order to study complicated objects, we can transform them into simpler objects. Each transformation is a mapping from an original complicated object to a simpler object, known as function. Now, for this transformation to be relevant, it needs to preserve some of the structures of the original complicated object. If it does, we call it a morphism, because the form or structure of the simpler object it creates is similar to the original complicated object.
Hehe… We’ve already met three structures! First, we have talked about isometries, which are morphisms that preserve distances. Then, we have discussed the structure of group of the set of symmetries. This structure is preserved by group homomorphisms. Finally, we have mentioned symmetries preserving the form of the Japanese Bridge, and we could think more generally of symmetries preserving any geometrical figure, as displayed in Marcus du Sautoy’s talkª. And there are many more structures to study! Examples of other morphisms include continuous functions for topology, diffeomorphism for smoothness, homomorphism for algebric structure (group, field…), linear transformation for linear algebra, cryptomorphism for information… If you can, please write about them!
An automorphism is a morphism which satisfies two more properties.
An automorphism needs to be bijective. Bijective morphism are called isomorphism. They are essential to category theory as they say that one set has the exact same structure than another. Any result on the structure of one is a result for all isomorphic structures. For instance, harmonic oscillators are isomorphic to spring oscillators in mechanics and RLC circuits in electricity. These problems are all similar, and solving one would solve the others. In mathematics, a major example is the fact that all normed vector spaces in finite dimension are isomorphic in terms of linear algebra and topology. Another tremendously important isomorphism is continuous morphisms with continuous inverse, called homeomorphism.
In terms of group theory, this condition corresponds to saying that symmetries need to be invertible.
Indeed. The second condition states that an automorphism needs to be an endomorphism.
An endomorphism is a morphism which compares an object with itself. That’s basically what we did when looking at fractals and saying that smaller structures were similar to larger ones. Thus, an endomorphism is a function from a set to itself. For this reason, we can think of applying successively two endomorphism: That’s the composition of endomorphisms! Get it?
Sure! Since automorphisms are bijective endomorphisms, they compare very well objects with themselves. Plus, this gives automorphisms are structure of group. This makes them very interesting to study. In fact, a whole field called pure algebra aims at improving the understanding of this structure. One of the major tool to analyze groups is through group representations, which has led to major breakthroughs such as the classification of finite groups or the proof of Fermat’s last theorem.
Below is a graph whose symmetries correspond to a sporadic group of automorphisms, i.e. a group that was hard to classify:
Let’s conclude
Symmetries are beautiful features of objects. I even wonder if our brains are trained to detect them subconsciously and to appreciate them. This would explain their presence in most of our arts. For mathematicians, symmetries are also useful, as they can simplify theoretical analyzes a lot. It’s especially the case in Fourier analysis, in which the description of any signal can be done by a set of trigonometric functions. These trigonometric functions are very similar to each other, very symmetric. This enables a very efficient study of signals. In physics, in cases of energy minimization, such as for bubble soap forms:
However, symmetries would be boring without… asymmetries. In cosmology, a major problem is actually finding these asymmetries in systems which are apparently highly symmetric. For instance, theories claim that, slightly after the Big Bang, the Universe was totally symmetric. But if it were, and if space was symmetric, then the Universe should have remained highly symmetric, and, in particular, would not have concentrations of matters in galaxies and stars. Another example of research of asymmetry in physics regards matter and antimatter. Matter and antimatter are totally symmetric and should therefore be present in equal quantities. Yet, matter is now much more present than antimatter. There must be an asymmetry for that. That asymmetry is something physicist are searching for.
There is another field in which symmetries are a nightmare: optimization. Indeed, symmetries lead to multiple solutions with same values. In linear programming for instance, this leads to high degeneracy (of the dual program to be accurate). This implies long complexity time. Similarly, in integer programming or constraint programming, branch and bound becomes a nightmare as symmetries imply a high number of branches which will need to be searched through. In such cases, imposing asymmetries is essential to accelerate complexity time. This is, for instance, what’s been done to prove that sudokus need at least 17 clues to be uniquely completable.
Many mathematical objects can be thought as a composition of a symmetric part and an asymmetric part. This gives a simpler way of understanding the objects. But I wonder if this isn’t also the sort of decomposition that’s subconsciously made by our brains.













Leave a Reply