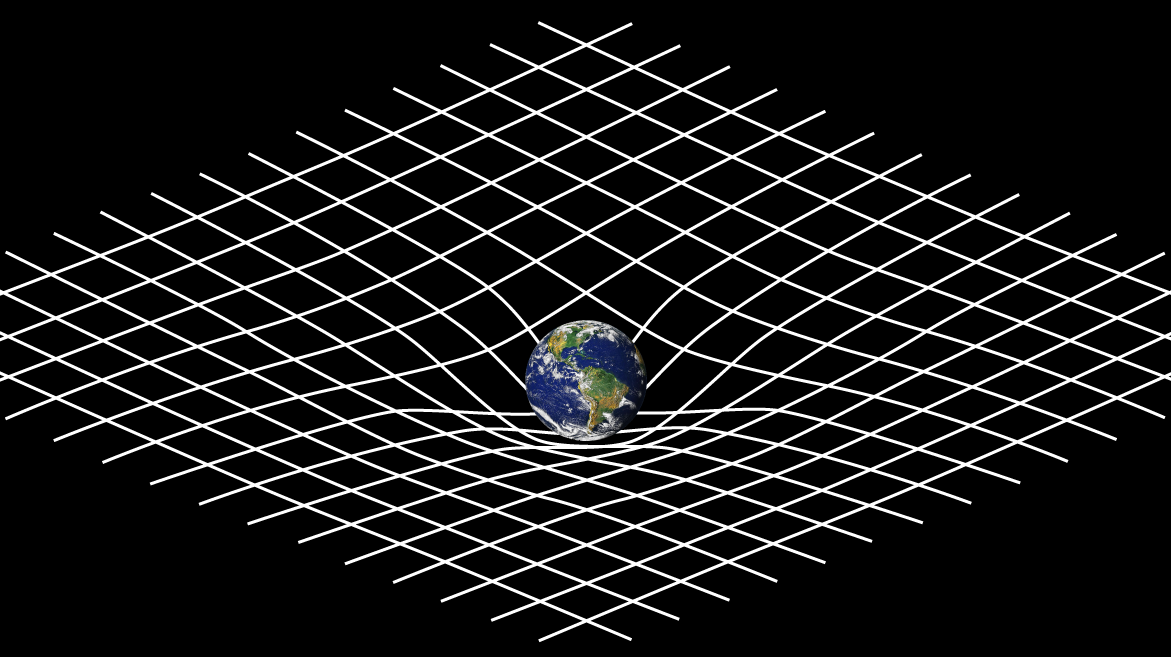
General relativity is commonly represented in popular science as in the following extract of the Fabric of Cosmos, what is space? hosted by Brian Greene:
But a few years ago, I read somewhere that this usual visual representation of spacetime as a bent sheet of cloth was wrong. Worse than that, not only was it wrong, it was also deeply misleading. Indeed, this representation works only if we consider that objects on the sheet are pulled down… by gravity! And yet, Einstein clearly stated that gravity was not a force!
It is! So, lately, I’ve decided to dig a little bit deeper into the theory of general relativity to come up with new representations which would be less misleading… And this will take us into the beautifully harmonious mathematics of general relativity!
The Spacetime Manifold
In these representations, time and space are separated! Yet, Einstein taught us that space and time are rather mixed together in a fabric he called spacetime. And, just like it doesn’t make much sense to talk separately about the rhum and the lime juice in a mojito, we should not talk about space and time separately. If you’re familiar with special relativity only, you might have thought of this mixing as a commodity. I know I did. In general relativity though, this mixing is more than essential to have a clear insight in Einstein’s thoughts.
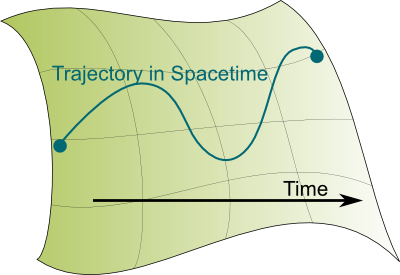
This means that the Universe is made of a spacetime in which we follow trajectories.
Yes. At any given time, we have some position in spacetime. But as time flows by… we are moving in time! Or, more accurately, in spacetime! By tracing all our successive positions, we are drawing our trajectory in the spacetime of our Universe. How poetic is that?
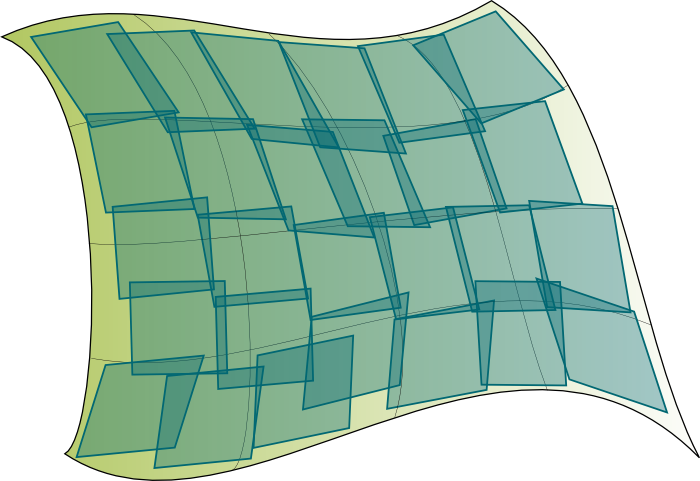
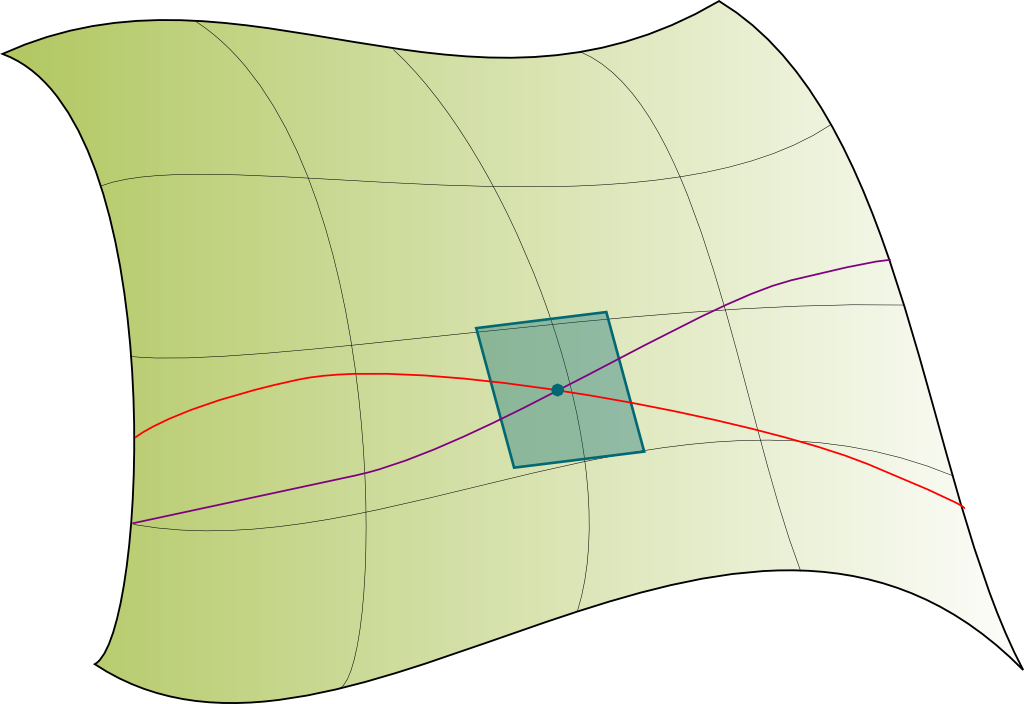
Our spacetime is in 4 dimensions, and that’s hard to visualize indeed. So, in this article, we’ll stick with a curved 2 dimension spacetime to illustrate Einstein’s general relativity, like the one on the right, where I drew a possible trajectory in spacetime.
That’s where we need a bit of differential geometry.
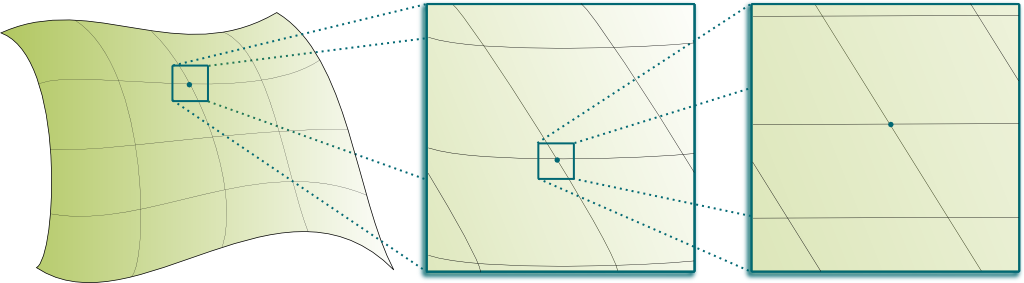
Don’t be scared! It’s not! If you’ve read my article on differential calculus, you should expect me to associate the word differential with something that looks like a line when you zoom in. This is precisely what differential geometry is.
Pretty much! For instance, the Earth is round. But when you zoom in on Google Earth, its roundness eventually disappears, and you end up with a flat two-dimensional surface. Similarly, Einstein’s great insight was to imagine that our spacetime appeared flat to us, only because we are too small to notice its roundness. In some sense, as explained in Scott’s article on map-making, his breakthrough is very similar to the Greek’s discovery of the roundness of the Earth!
Imagine that, on the curved 2D spacetime I showed earlier, small creatures were living and were too small to notice that their spacetime was in fact curved. They would feel like living in a flat 2D spacetime, as illustrated below:
In mathematics, such objects which look flat when we zoom in are called manifolds. As Scott explained it in his article on the geometry of general relativity, what makes reasonings difficult is that we are embedded in our 4D spacetime. In fact, the visual 2D spacetime example above is already a misleading simplification of what manifolds can be, as most 2D manifolds cannot be embedded in our 3D space. But it’s the best visual example I can offer!
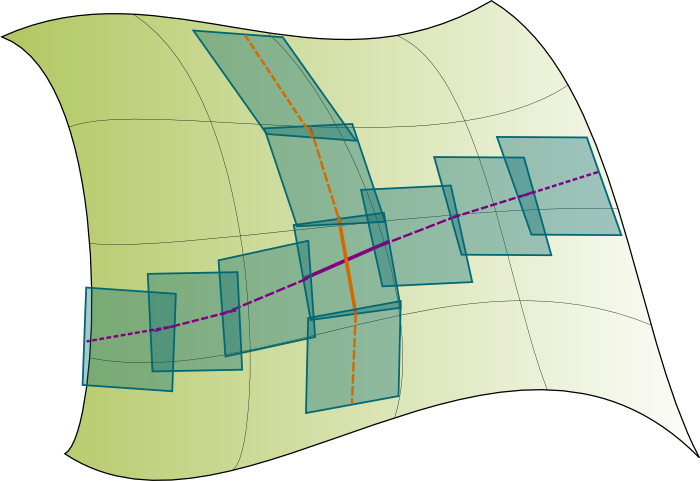
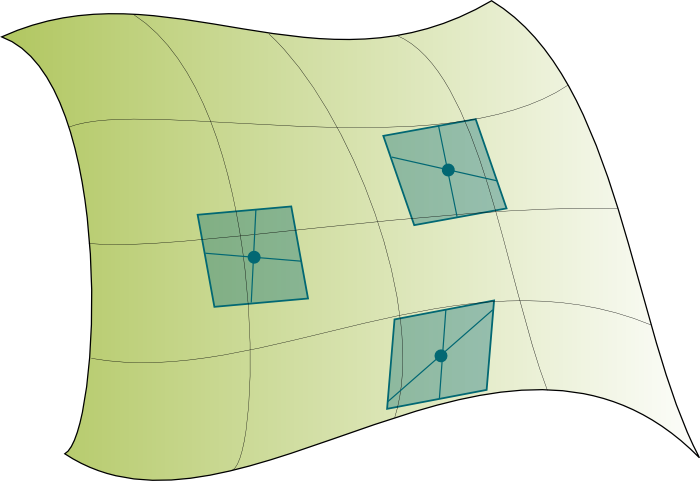
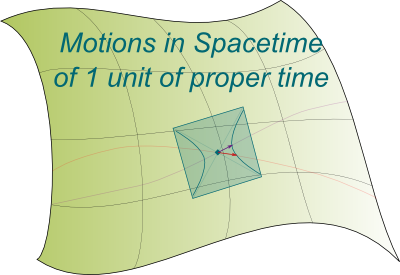
But we can sort it out! Using the zooming-in property I mentioned earlier, we can say that at each point in spacetime, spacetime seems like a flat vector spacetime called tangent spacetime. There is a tangent spacetime associated to each point in spacetime! These tangent spacetimes are essential as they can be regarded as the building blocks of spacetime! As illustrated on the right.
Tangent spacetimes are simple. I mean, relatively simple. Indeed, they are vector spaces which can be described by special relativity. Motions in these tangent spaces of objects on which only gravity acts are simply lines.
We’ll see later that the description involving the metric tensor requires us to use vectors. But, by using affine connections, we can directly work with straight lines in tangent spacetimes! That’s much simpler and more intuitive!
Indeed. The tangent space is only valid for small scales. Thus, so far, we can only describe how motions work in all the small tangent spacetimes which fill spacetime, as displayed on the right. To go further, we need to connect tangent spacetimes. This is done using an affine connection.
Affine Connection
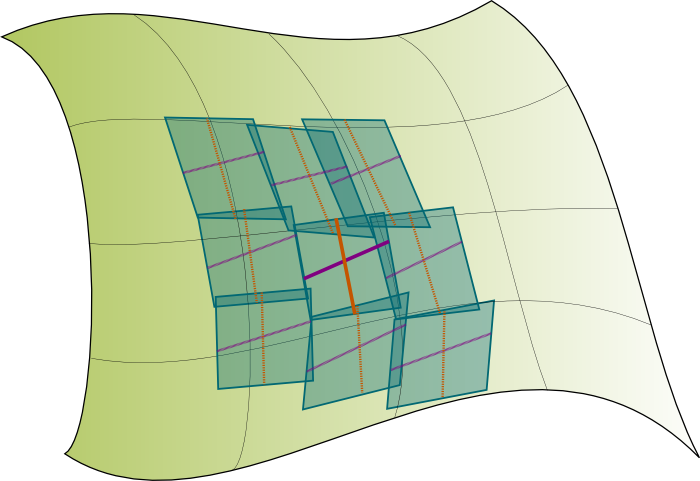
An affine connection tells how a direction is moved from a tangent spacetime to a neighbour tangent spacetime. This deformation is similar to a spacetime deformation in special relativity, as I explained it in my article on space deformation and group representation.
On the right is illustrated the affine connection of a tangent spacetime with its neighbour tangent spacetimes. In particular, I’ve represented how the orange and purple directions get transformed when moved to neighbour tangent spacetimes. We say that the orange and purple directions undergo parallel transports to neighbour tangent spacetimes. Here’s an explanation I gave on my Youtube channel:
Through the concept of differentials! Basically, starting at an original tangent spacetime, for one step in any direction of spacetime, the affine connection is an operator which tells how directions are moved into the new tangent spacetime. And because this deformation is proportional to the length of the step, it’s described by a differential. This differential describes how the motion is moved. Or, equivalently, the motion of the motion!
Yes! More precisely, the affine connection is a differential of motions in tangent spacetimes. It maps a motion and the direction in which the motion is moved with variation of the motion. The affine connection is thus formally a mapping of a tangent spacetime and 2 motions in it with 1 motion of the first of the two motions in the direction of the second (take your time to read this phrase!). This is why we call it a tensor (1,2).
It nearly does! The only concept you need is the simplest one: When only gravity acts upon an object, the object always moves in straight line in spacetime. Or rather, its trajectory never gets curved in its own tangent spacetime, and it moves to its next tangent spacetime, while remaining parallel to itself. But, from the perspective of another observer, the successive tangent spacetimes of the trajectory do get curved!
Yes, although they are usually rather defined differently! But I prefer to see geodesics as trajectories which are always going straight in tangent spacetimes. The picture on the right illustrates two geodesics, constructed based on this idea.
We are now ready to describe Einstein’s equation…
Einstein Equation
Hummm… Don’t set your hopes to high… To really describe Einstein equation, I’d need to introduce even more tensors like the metric tensor, the Riemann tensor, the Ricci tensor, the Einstein tensor and the stress-energy tensor. And those are all very hard to visualize. At least for me.
Still, this won’t stop me from telling you the important message of Einstein equation: Energy is what bends neighbour tangent spacetimes!
Einstein’s famous formula $E=mc^2$ actually says that mass is just a form of energy.
Let’s take an example on a 2D spacetime. Let’s track the trajectories of a Sun and its Earth in this spacetime. From its perspective, its trajectory is a line. Now, let’s consider an Earth influenced by the gravity of the Sun. Because no force acts on the Earth, it is moving straight in its tangent spacetime. However, its tangent spacetime gets deformed towards the Sun because of the gravity caused by the mass of the Sun. This is displayed in the following figure:
I’m not sure. As I said, considering 2D spacetime manifolds as a sheet is nice to introduce the idea of curved spacetimes, but it’s misleading since most 2D manifolds can’t even be represented in our 3D world. That’s where you need to make a quantum leap by considering the spacetime manifold as something that locally looks like a vector space, but does not have an easily describable global structure. This global structure is rather described by differential topology, and its study often poses difficult open problem such as the Poincaré conjecture.
Yes! In particular, each direction in tangent spacetimes is rotated towards the mass. So, if you think about our actual Earth, we are moving straight, and rather than a force pulling us towards the Sun, there are gravitational waves coming from the Sun which, from its perspective, bend our tangent spacetime as we move in time. Now, to go even further in the understanding of general relativity, I should talk a bit more about space and time.
Space and Time
Our spacetime has an additional structure which is inherited from special relativity and is due to the speed of light being a fundamental limit of spacetime. More precisely, tangent spacetimes are ruled by special relativity.
Now, if you have read my article on special relativity, you know that an essential element to describe special relativity is…
No! Even us dummer people can figure it out! Provided we use…
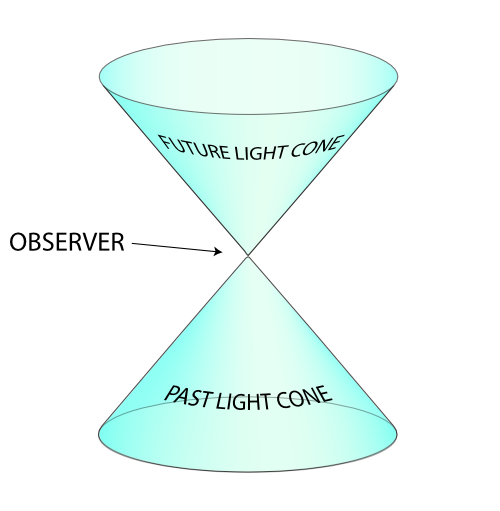
Yes! This is an important feature of spacetime of general relativity! At each point in spacetime, spacetime around looks like a 4D vector space with a light cone defined. This light cone is essential because it separates spacetime into 3 components: space, future and past. Needless to say these three components are very different. Thus, we distinct the motions in spacetime in four categories:
- Motions in space, called spacelike vectors: they point towards the outside of the light cone.
- Motions at light speed, called null vectors: they point along the borders of the light cone.
- Motions towards the future: they point towards the upper inside of the light cone.
- Motions towards the past: they point towards the lower inside of the lightcone.
The two last motions are motions in time, and they are called timelike vectors.
On the right is the image of the light cone in a 3D spacetime taken from wikipedia.
That’s because Wikipedia’s image is misleading! In fact, the mere idea of spacetime made of 1 direction of time and 3 of space is very misleading. What’s usually meant by that is that the most natural and useful ways to decompose spacetime are by using 1 direction of time and 3 of space. But as explained by Henry Reich on Minute Physics, there is no “fourth” dimension. In fact, you could generate spacetime with 4 timelike vectors! If you’re familiar with vector spaces, this shouldn’t be hard for you to see…
Yes! There’s no such thing as the arrow of time. Rather, there are a bunch of arrows of time at each point in spacetime.
Yes. This is what makes spacetime a Lorentzian manifold of signature (1,3), and is equivalent to saying that there is a light cone decomposing spacetime in 3 components. Learn more with my article on space deformation and group representation.
Sorry but motions in space aren’t going to happen! Einstein’s postulate which says that nothing goes faster than light in tangent spacetimes implies that we can’t have motions in space. Light is just fast enough to move along the light cone. But objects with mass like us can only move in time. And because motions are all relative, there is no way of saying that they move less in time and more in space than others. But to better understand this relationship between space and time, we need to involve the metric tensor I have been avoiding so far.
The Metric Tensor
To understand the metric tensor, let’s restrict ourselves to motions in time. After all, only these are the ones which make sense…
It compares them! More precisely, if two trajectories in spacetime (not necessarily geodesics) meet at a point, then the metric tensor at this point can tell how fast a trajectory is moving compared to the other. Now, if you are familiar with special relativity, then you should know that, rather than the relative speed $v$, we rather equivalently work with the Lorentz factor $\gamma = (1-v^2/c^2)^{-1/2}$. The metric tensor is precisely the mapping of any two trajectories and a meeting point with this value $\gamma$.
That’s because I’ve simplified it. Technically, we need to map the trajectories at the meeting point with a vector which indicates the direction of the trajectories. Now, assuming that the future is well-defined, we only need to find a normalization of this vector. In this setting, at each point in spacetime, the metric tensor has to be viewed as a bilinear form which, when applied twice to the same vector gives a sort of square of the norm of the vector.
The obtained norm of a vector can then be interpreted as the proper time of path passing by this vector.
Yes! The concept of time really depends on the observer. And the proper time of an observer is how the observer perceives his own time.
An observer is basically another object which will follow another path in spacetime. Now, if you are moving in a parallel direction from him in spacetime, then you’re not moving in space relatively to the observer. Thus, you’ll be moving a lot in time. On the opposite, if you are moving in a very different direction in spacetime, then your time will be slowed from his perspective. This perturbing aspect is illustrated in the following extract from the Fabric of the cosmos – the Illusion of Time by Brian Greene:
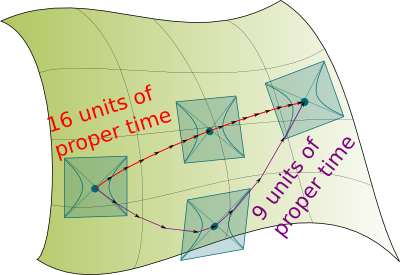
As explained by Brian Greene, time is not unique. In fact, each observer has its own time. More precisely, each trajectory has its own clock ticking. And the passing of time is measured by the norm of the vector. This leads us to a natural normalization of vectors of motions in time, by fixing their proper times to be equal to 1. These vectors of motions in time with proper time 1 correspond to a 3D hyperboloid. On the right is represented a 1D hyperboloid at the tangent spacetime where the trajectories meet (there are two sheets, one for the past, the other for the future).
The coefficient $\gamma$ is then obtained by applying the bilinear form of the metric tensor to the vectors of motions of one unit of proper time. In other words, we first need to normalize the vectors of motions before computing $\gamma$.
Geodesics between two points which can be joined with a trajectory in time are trajectories which maximize the proper time! Visually, you can see that if we zigzag, the steps of one unit of proper time are greater and we can get from a point in spacetime to another in little proper time. On the contrary, the more direct path takes more proper time.
Using the Euler-Lagrange equation which computes geodesics of points extremely close, this condition of proper time maximization can then be translated as a relationship between the affine connection and the derivatives of the metric tensor. This implies that the knowledge of either the affine connection or the metric tensor uniquely defines the other. Overall, both are defined by the distribution of masses and energies in the universe, accordingly to Einstein equation.
Yes! I mentioned it in my article on special relativity, but, now that we have explained general relativity, we can explain it accurately!
Sure. The twin paradox says that if two twins are born at the same point in spacetime, take different paths in spacetime and then meet again, then both would be still in their inertial system. Thus, both should have time flowing faster than the other’s.
You’re totally right! In the setting of general relativity, there is absolutely no paradox. And it’s quite easy to resolve the apparent paradox. If one of the twin stays on a planet while the other is travelling around the universe, the settled brother is nearly following a geodesics and thus maximizes its proper time. Time will thus flow faster for him. And when they’ll meet again, he’ll be older.
Indeed! Think about satellites. No force acts on them. Thus, they really follow geodesics in spacetime. Meanwhile, on Earth, we oppose gravity by standing on the surface of the Earth. This means that we divert from geodesics by using the electromagnetic forces that prevent us from crashing towards the center of the Earth. Thus, our time isn’t maximized as is the time of satellites. Time thus flows slower for us than for satellites. Taking this distortion of time into account is essental for GPS, as explained by Henry Reich on Minute Physics.
Let’s Conclude
We have got through the main ideas of general relativity! How awesome is that?
Frankly, when I started this article, I was quite scared, not only to be able to make it simple, but also simply of how well I understood general relativity. I’ve never had a course in general relativity. All I did is read through this introduction in French. But I feel like I’m providing here a description which is very faithful to the mathematical one! Now, I’m absolutely no expert in this field, and if you do master this beautiful theory, I’d love your feedbacks! Obviously, I skipped the difficulty of actually explaining Einstein equation, and the reason for that is that I myself can’t really visualize it (especially the Ricci tensor!). But if you can, please do!
Well, in fact, when you really get into it and appreciate its amazing beauty, I’d say that it’s hard not to! It’s worth mentioning that it took several years to confirm this theory. In fact, general relativity was first refuted twice! Today, it’s one of the two foundations of theoretical physics, and is impressively accurate for large scale observations. And I hope you’ll now have goose bumps when you hear physicists talk about it and you’ll be thinking: I kind of get what they’re talking about!
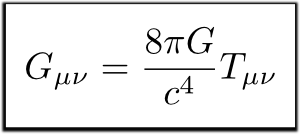

Leave a Reply