In several decades, 2013 might be considered mathematically Historical. For an entire year, three dozens of 2013’s greatest minds were gathered at the Institute of Advanced Study in Princeton, with the duty to rethink the foundations of mathematics!
They surely did! And it’s all contained in a massive 600-page new Bible of mathematics you can download for free! This holy book shatters much of the classical edifices, and redefines many of the most fundamental concepts of mathematics, like equalities. More interestingly, it gives a new powerful paradigm for what mathematics is, and how it should be structured. This paradigm sounds so promising that, in April 2014, the Department of Defense has given Carnegie Mellon a 7.5 million dollar DoD grant to carry on the ideas of this new paradigm!
To understand the importance of redefining the whole endeavor of mathematics, let’s go back a hundred years…
The Math Foundation Crisis
In 1901, Bertrand Russell (a future winner of the Nobel prize in literature!) annihilated all previous mathematics which a destructive one-line argument. With this single line, he refuted the thousands of pages of (naive) set theory which took decades for Georg Cantor and Gottlob Frege to develop. Thereby, this line also rashly disproved the foundational logic that mathematics was supposed to build upon!
I know! Yet, somehow, the fact that a single line can destroy centuries of thoughts and thousands of books… That’s part of the cruel and unique beauty of mathematics.
Russell tried his best to do so. For decades, he combined his force with Alfred Whitehead to rigorously redefine the foundations of mathematics, which they published in the Principia Mathematica. But that was unbelievably tedious work! For instance, it took 362 pages for them to finally prove the identity $1+1=2$.
That was the cost of rigor! To make sure that everything they wrote was perfectly logic, Russell and Whitehead had to patiently verify everything. At least they tried…
It took the greatest logician of all times to prove that they didn’t. In 1931, the young Kurt Gödel crushed Russell’s dreams of a flawless mathematical theory, by proving the famous incompleteness theorems. In short, the first incompleteness theorem states that any mathematical theory including numbers must have claims which can neither be proved nor disproved. Worse, the second proves that no such mathematical theory could ever be proved to be consistent. Naturally, these theorems asserting the impossibility to put mathematics on unshakable grounds led Russell to the following conclusion:
Since then, the most popular foundation of mathematics is a (more consistent) variant of Frege’s naive set theory called the Zermelo-Fraenkel (ZF) theory. Even though mathematicians have no proof that this theory makes sense, and because they know they’ll never have such a proof, most consider ZF to be true, or, at least, correct. For many, ZF is what current modern mathematics is built upon.
Importantly, ZF set theory essentially defines the objects of mathematics as sets, and discusses how they relate with one another through propositions and the infamous membership relationship “$\in$”. However, in the 1950s, an alternative foundational theory called category theory emerged, mainly with the impulsion of the giant Alexander Grothendieck. Interestingly, objects were no longer the core of this foundational theory of mathematics, as asserted by Jean-Pierre Serre:
I guess that searching for the foundations of mathematics, which is the basics of all science, has to be philosophical! After all, it’s about what mathematics is, or, even, what it should be. In fact, a crucial philosophy of mathematics dates back from Luitzen Brouwer. It is called intuitionism, and asserts that the whole endeavor of mathematics is inevitably human-driven. So, mathematics should not be about seeking some absolute Platonic truth that is out there (which was Gödel’s philosophy), but, rather, it should be about what, as humans, we can construct. This effectively gave birth to constructive mathematics, in which all objects must be constructed (or constructible).
Hummm… I’d rather say that ZF and category theory are not really suited for constructive mathematics. A controversial example of a difference between a classical ZF reasoning and a constructive one has to do with the law of excluded middle. This law asserts that what’s not false is true. This leads to Euclid’s famous proof by contradiction: To prove the existence of an object, it suffices to prove that the assumption of its non-existence implies a contradiction. Although this sounds intuitively right, constructive mathematicians instead point out that such proofs do not yield an instance of the existing object. They do not construct the object. For this reason, they are pointless, and we should not do mathematics accordingly to such proofs. Not false is not necessarily synonym to true. I know this sounds counter-intuitive, but, after all, the existence of a third alternative to (provably) true and (provably) false is just the direct implication of Gödel’s first incompleteness theorem.
It is! And fortunately, type theory draws a clearer picture of the fuzzy world of logic. To do so, roughly, it encapsulates each mathematical theory into a universe. One universe may satisfy the law of excluded middle. But another may not. The beauty of type theory is that it is perfectly fit to describe both.
Crucially, type theory models both objects and the relations between them with types. Thus, a type can be a set or a theorem (or something else). And proving a theorem boils down to constructing a term of the theorem type.
Let me clarify something. Construction in type theory is not synonym of constructivism in Brouwer’s intuitionism (this latter is what is usually meant by constructive mathematics). Suppose that we have proved that assuming 10 is the biggest number leads to a contradiction. In other words, the claim that there is no number bigger than 10 us false. Then, Brouwer’s intuitionism asserts that this proof cannot construct a number bigger than 10, and the proof is thus useless. But we can add the law of excluded middle in type theory as a function which (type-theoretically) constructs some number $x$ bigger than 10 from the proof by contradiction. Conversely though, type theory without excluded middle will not enable that construction of $x$ from a proof by contradiction.
Homotopy type theory consists in studying a type theory universe with a single axiom (as opposed to the 8 axioms of ZF theory)! This axiom, which, by the way, is extremely elegant, is called the univalence axiom. Loosely, it asserts that equivalent types are identical. In essence, this builds upon the famous quote by the father of homotopy theory, the great Henri Poincaré:
Amusingly, Henri Poincaré was also both a great opponent to set theory, and, more importantly, the father of homotopy theory. I bet he would have loved homotopy type theory!
Type vs Set Theory
In this article, we won’t get to homotopy type theory. Instead, we’ll focus on type theory, which was first investigated by Bertrand Russell. But it has greatly evolved since, and represents today the main alternative to set theory.
For a long time we didn’t. In fact, by adding or removing the right axioms in set theory, it seemed like we could get all sorts of mathematics, and Gödel’s second incompleteness theorem guarantees that we’ll never find any more consistent alternative foundation theory. So, the point of an alternative foundation theory cannot really be about creating more mathematics, and definitely not about making mathematics more consistent.
For computational reasons. The rise of computers raised great interest for type theory, because it better fits computational programming. In particular, proofs in type theory are sequences of instructions, which can be implemented and checked computationally, hence guaranteeing their validity. This computationally-checkable new paradigm may revolutionize the way mathematics is done! In fact, I’m guessing that 22nd Century mathematicians will look down on us and wonder how we ever did maths without this paradigm, just like we (or, at least, I) wonder how 20th Century mathematicians managed to write books without text editors!
Modern mathematics now regularly faces proofs that only a handful of mathematicians can (or is willing to) verify, like in the examples of Hilbert’s 16th problem or Mochizuki’s ABC conjecture proof. This has been particularly the case in computerized proofs like those of the 4 color theorem, the Kepler conjecture or this recently found wikipedia-size proof. Meanwhile, checking proofs of the Millenium prize problems require years, and, in many cases, flaws end up revealed. Plus, while it’s definitely important for proofs to drive our intuitions, we also have to acknowledge the fact that some proofs are simply beyond human comprehension, and it may be relevant enough to merely know that they are correct.
Because set theoretical proofs are really not adapted to computation, mainly because many sentences in set theory are meaningless. This lack of structure within set theory means that programming it would be like writing codes without programming structures. It’d be messy, uncorrectable and nearly impossible to build upon.
I’ve never done that… But the authors of the book have successfully computationally checked all the proofs of their 600-page book! And, what I can assure you, is that many of these proofs are very nontrivial modern mathematics proofs! Plus, I guess that they have laid out most of the groundwork, and it will then be easier for others to build upon that. There’s an analogy here with what the first programmers did for computer science, as they wrote the hardcore basic Assembler codes others have built upon since.
It is! But its practicality isn’t the nicest fact about it! What’s much more important, at least to me, is that (homotopy) type theory yields a beautiful different perspective on mathematics.
Hehe…
Types
Type theory is a huge abstract lego game, which aims at constructing terms of (interesting) types from other already constructed terms. For instance, terms of the type $\mathbb N$ of natural numbers are constructed either as the term $0:\mathbb N$, or as a successor $\mathsf{succ}(n):\mathbb N$ of some already constructed term $n \in \mathbb N$. This means that, to construct the number $2: \mathbb N$, we need to start from $0: \mathbb N$, then construct $1 :\equiv \mathsf{succ}(0) : \mathbb N$, and then $2 :\equiv \mathsf{succ}(1) \equiv \mathsf{succ}(\mathsf{succ}(0)) : \mathbb N$.
There are plenty of subtle differences I won’t dwell on too much here. But, most importantly, saying $x: \mathbb N$ means that $x$ is by definition the result of a finite construction like the one above. In fact, it’s useful to consider that the letter $x$ stands for the entire construction, and not merely as the result of its construction.
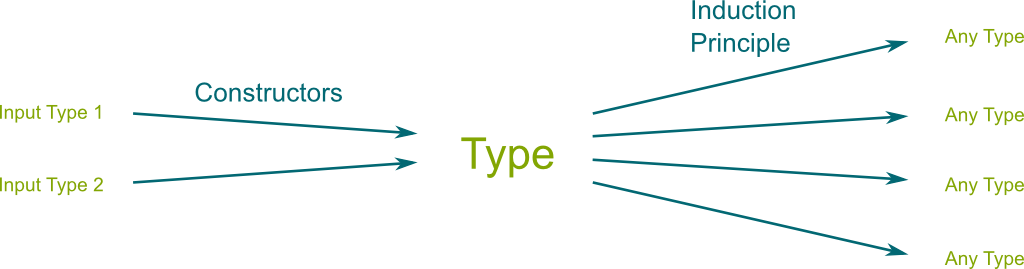
Now, constructing terms is nice, but it’s useless unless we know how to manipulate them. Thus, while constructors of natural numbers are functions $? \rightarrow \mathbb N$ which output a (new) number, as in $\mathsf{succ} : \mathbb N \rightarrow \mathbb N$, we also need to determine how we can define functions $\mathbb N \rightarrow ?$ which input natural numbers. This way to define outgoing functions is called the induction principle (or elimination principle, or recursion principle).
Sure! For instance, to define a function $f : \mathbb N \rightarrow \mathbb R$, we are going to need to construct the images $f(0)$, $f(1)$, $f(2)$… successively. This will be very similar to the way we constructed $0$, $1$, $2$… themselves. First, we need to determine the first term $f(0) : \mathbb R$. Second, we need to define how $f$ uses the value $f(n): \mathbb R$ obtained for $n : \mathbb N$ to compute $f(\mathsf{succ}(n)) : \mathbb R$. Calling $g : \mathbb R \rightarrow \mathbb R$ the function which defines the next term, we have $f(\mathsf{succ}(n)) :\equiv g(f(n))$. The data $f(0):\mathbb R$ and $g : \mathbb R \rightarrow \mathbb R$ then define the function $f$.
Let me finish this section by a figure which recapitulates what characterizes a type.
Definitional Equalities
Now, following Poincaré’s quote, mathematics mainly boils down to determining what (different) constructions can be given the same name.
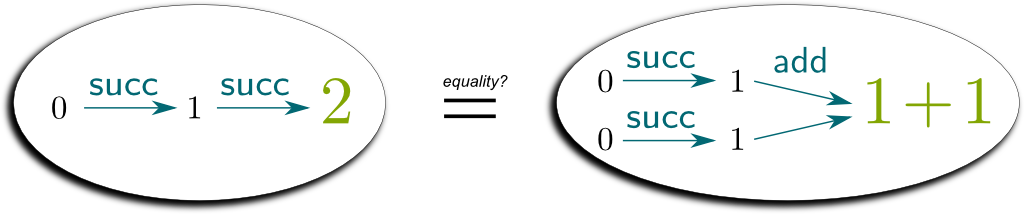
So let me give you an example. Let’s compare the constructions of $2: \mathbb N$ and $1+1: \mathbb N$:
As it turns out, in this case, the two constructions are somehow equivalent.
Yes. To prove that, we need to get to the definition of addition. There are actually many ways to do so. One way consists in defining $\mathsf{add}(m,n)$ using the induction principle on $n:\mathbb N$.
We need a first term which we defined by $\mathsf{add}(m,0) :\equiv m$. Then, given $x \equiv \mathsf{add}(m,n)$, we construct the next term by $\mathsf{add}(m, \mathsf{succ}(n)) :\equiv \mathsf{succ}(x)$. This corresponds to using the function $g \equiv \mathsf{succ} : \mathbb N \rightarrow \mathbb N$ to construct next terms in the sequence $\mathsf{add}(m,0)$, $\mathsf{add}(m,1)$, $\mathsf{add}(m,2)$…
In the sum $1+1$, $m$ has been replaced by $1$ and $n$ by $1$. We now use the induction principle. Since $1$ is the successor of $0$, we are in the second case of the definition of $\mathsf{add}$. Therefore, we have $\mathsf{add}(1,1) \equiv \mathsf{add}(1, \mathsf{succ}(0)) :\equiv \mathsf{succ}( x )$, where $x \equiv \mathsf{add}(1,0)$. Yet, to compute $\mathsf{add}(1,0)$, we find ourselves in the first case of the induction principle. Hence, $x \equiv \mathsf{add}(1,0) :\equiv 1$. Therefore, $\mathsf{add}(1,1) \equiv \mathsf{succ}(x) \equiv \mathsf{succ}(1)$. This last term is, by construction, 2. Therefore, we have $1+1 \equiv 2$.
Identity Types
Yes. A big one. The definitional equality $1+1 \equiv 2$ holds by construction. In other words, it says that the sequence of constructions involved in defining $1+1$ is exactly the same as the one for $2$. However, and that’s where things get tricky, the propositional identity $1+1=2$ is actually a type, with possibly terms belonging to it. Crucially, as opposed to definitional equalities, an identity can be proved (or disproved, by that’s much trickier!). To prove an identity, we need to construct one of its terms.
Terms of identity types are called proof or witnesses (or, as we’ll see, paths). Now, naturally, the simplest kind of proof is the one that asserts that two identical constructions are equal. For instance, since by construction $1\equiv 1$, we have a proof $\mathsf{refl}_1$ of the type $1 = 1$, and we can write that fact compactly as $\mathsf{refl}_1: (1=1)$ (parentheses are usually dropped). Similarly, since $1+1 \equiv 2$, we have a proof $\mathsf{refl}_2 : 1+1=2$. Finally!
This will enable us to prove many more things! For instance, let’s prove that $0+n=n$ for all $n:\mathbb N$. To do so, for all $n:\mathbb N$, we need to construct a proof $f(n)$ of the type $0+n=n$.
“Obvious” is a dangerous word in foundational mathematics!
Don’t worry, I’ll go slowly. To prove $0+n=n$, once again, we are going to use the induction principle of $\mathbb N$ to construct the function $f$ which maps $n:\mathbb N$ with a proof $f(n):0+n=n$. Recall that to construct such a function, we need to specify its first term $f(0)$ and a way to construct the terms $f(\mathsf{succ}(n))$ from $f(n)$.
The first term $f(0)$ needs to belong to the identity type $0+0 = 0$. Using the definition of addition, we know that $\mathsf{add}(0,0) :\equiv 0$, thus, by definition, we have $0+0 \equiv 0$. Now, we use the fact that identical constructions yield a proof of the identity types. This gives us a proof $f(0) :\equiv \mathsf{refl}_0$ of $0+0 = 0$. Our first term of the function $f$ has been successfully constructed!
Exactly! By induction, we are given a successfully constructed term $f(n) : 0+n=n$. Now, notice that $\mathsf{add}(0,\mathsf{succ}(n)) :\equiv \mathsf{succ}(\mathsf{add}(0, n)) \equiv \mathsf{succ}(0+n)$. Thus, by replacing each side by definitionally equal terms, the identity type $0+\mathsf{succ}(n) = \mathsf{succ}(n)$ is actually definitionally equal to the identity type $\mathsf{succ}(0+n) = \mathsf{succ}(n)$. Now, intuitively, if $0+n$ is equal to $n$, then applying some function to both preserves equality.
It’s actually the essence of the propositional identity. More precisely, it is an immediate consequence of the induction principle of identity types: If there is a proof $p$ that $x = y$, then, for any function $g$, we can construct a proof $q$ that $g(x) = g(y)$. The property is known as the lemma of action on path. Now, don’t forget that $x$ and $y$ (and $p$) stand for constructions, and that $g(x)$ and $g(y)$ simply consists in adding one step in these construction. Then, visually, the action of path corresponds to the following figure:
Let’s conclude our proof that $0+n=n$. We have given a proof $f(0): 0+0=0$. Plus, using action on path, we have shown how to construct a proof $f(\mathsf{succ}(n)) : \mathsf{succ}(0+n) = \mathsf{succ}(n)$ from a proof $f(n) : 0+n=n$. Thus, using the induction principle of the type $\mathbb N$, we have constructed the function $f$ which maps each natural number $n$ to a proof of $0+n=n$. Woohoo!
This is exactly what we did. And amusingly, in type theory, using propositional identities, proof by induction is merely a case of function construction.
Logic
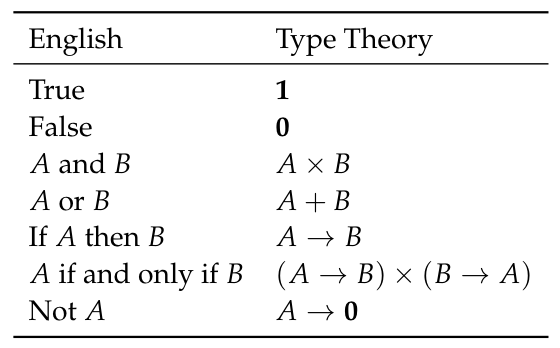
Now, what the example tells us is that logical implications can merely be regarded as functions. After all, to prove that $n:\mathbb N$ implies $0+n=n$, we constructed of a function $f$ that inputs $n$ and outputs a proof of the identity type $0+n=n$. More generally, type theory considers that a type $A$ is true if and only if it is inhabited by a term $a:A$. Then, the logical implication $A \Rightarrow B$ perfectly matches the existence of a function $f: A \rightarrow B$ which constructs a term of $B$ (and thus proves $B$) from a term of $A$ (and hence the assumption that $A$ is true).
They have type theoretical translations too! The logical expression “$A$ and $B$” corresponds to the type $A \times B$ called product. Meanwhile the logical proposition “$A$ or $B$” resembles the type $A + B$ called coproduct. This coproduct is to the set-theoretical disjoint union of $A$ and $B$.
Negations are very tricky. In fact, constructive mathematics avoids negations, mainly because negations are not… constructive! Formally, the negation of a type $A$ is defined as $\neg A :\equiv (A \rightarrow {\bf 0})$, where $\bf 0$ is the type with no constructor. In other words, a type $A$ is false if proofs of $A$ imply a construction of an element of the empty type $\bf 0$ (also known as a contradiction). With this definition, you can still prove that non-$A$ and non-$B$ is equivalent to non-($A$ or $B$). But…
You can no longer prove the other Morgan’s laws. In particular, there is no proof that non-($A$ and $B$) implies non-$A$ or non-$B$. In fact, crucially, it is no longer the case that the non-inexistence of an object implies its existence. More precisely, there is no proof that $\neg \neg A \rightarrow A$ for all types $A$.
Is it though? The beauty of mathematics is to question with reason the simplest facts that we believe to be intuitively obvious. And the last century of logic indicates that many such intuitive obviousness are at best unjustifiable, if not wrong. Today’s greatest minds have long thought it through, and concluded that we shouldn’t blindly believe that not-untrue claims are true…
Yes. To make it compatible, we simply need to add an axiom $\mathsf{LEM}$ for the law of excluded middle. For any type $A$, this axiom yields a proof $\mathsf{LEM}(A) : \neg \neg A \rightarrow A$. This proof (type-theoretically) constructs an element of $A$ from its double negation. In other words, once we’ve finished a proof by contradiction that some object exists, then $\mathsf{LEM}$ gives us an example of that object.
First-order logic in set theory defines two different quantifiers which are essential to mathematics. First is the symbol $\forall$ which reads “for all”, and which we used when we claimed that for all $n : \mathbb N$, we have $0+n=n$. There’s a type-theoretical way to say that. We say that the infinite product type $\prod_{n:\mathbb N} (0+n=n)$ is inhabited. But, in addition to a proposition of logic, it’s useful to regard this infinite product as the type of functions which input $n:\mathbb N$ and output a term (or, in this, a proof) of $0+n=n$.
Can’t you guess? The universal quantifier “$\forall$” corresponds to generalizing the product to infinite product. Similarly, the existential quantifier “$\exists$” in phrases like “there exists $n:\mathbb N$ such that $1+n=2$” corresponds to claiming that one of the types $1+n=2$ is inhabited. This can be expressed as the fact that the infinite coproduct type $\sum_{n:\mathbb N} (1+n=2)$ is inhabited.
Let’s Sum Up
It’s always hard to predict the importance of a new theory. Only time will tell. However, if I were to venture on a guess, I’d say that (homotopy) type theory will be a major cornerstone of 21st Century mathematics. I believe that its formalism will trigger a dialog with computers, which, in decades to come, will guide our quest for new insights into the breathtaking world of mathematics. Now, type theory is already pretty cool, but things become even more awesome if you add a homotopy dimension to it! For instance, the last chapter of the book redefines real numbers in a much more convincing way than any other theory ever has before. At least, that’s what the authors of the book claim, and I’m very tempted to believe them.
I’ll try! In one sentence, homotopy type theory is a beautiful attempt to formally redefine the whole mathematical endeavor in a way that is both much closer to how informal mathematics is actually done and to how mathematics should be implemented to be computationally checkable. It builds upon type theory, which asserts that both mathematical objects and their relations can be encapsulated in the concept of type.
For sure! Crucially, homotopy type theory allows much more freedom in the construction of types, by effectively constructing (and allowing) different proofs of a single (identity) type. But to get there, you’ll need to check the second part of the series!








Leave a Reply