Bayesian Games: Math Models for Poker

In card games, players have an incomplete information about the other players’ cards. This is actually the case in most games. Instead, players consider a probabilistic distribution over the incomplete information. In this setting, the concept of Nash Equilibrium no longer stands. To study such games, we need to change the way we think about players’ strategies. This requires a great change of perspective, which enable to rethink the way poker works, as explained briefly by French American professional law student and poker player Vanessa Rousso:

Now, poker is way too complicated to be studied in this article. So I’ll introduce two simpler games to better understand what bayesian games are and how they are modeled. This field is pretty much the intersection of John Nash’s world of game theory, Thomas Bayes’ world of probabilities.

Highest Card Game

Let’s start with a basic 3-players highest card game, between Vanessa, John and Thomas. We consider cards of heart only, from the Ace to the King, Ace being the smallest, as displayed below:

Each player is given one of these cards. Then, each player is asked to write on a sheet of paper whether he believes he has the highest card. He can either answer yes or no. These are his possible actions. So which actions do you think players will choose?

Indeed! The card each player receives is called its type. In a more general setting, this type corresponds to all of the player’s private information. As you said, a player’s best action depends on its type. This is a crucial remark which we’ll get to later. Right now, let’s assume players receive cards as follows:

Let’s do the reasoning for Vanessa (not that she needs me to…). She should say yes if her card is actually the highest card, that is, if her card is higher than both John’s and Thomas’. But without perfect information about other players’ cards, she needs to include probability in her reasoning. She’ll be assuming that the cards were well mixed, and thus, that the probability of the others’ cards being one of the 13 cards is 1/13. This is called the belief. This belief is updated with Vanessa’s knowledge of her own card.

Now, out of the 12 cards other than hers, there are 8 cards lower than 9. Thus, the probability that John’s card is lower than hers is 8/12. If it’s not the case, then the Vanessa’s card is not the highest. If it is, we need to go further in the reasoning.

So let’s assume that it’s the case, that is, John’s card is 8 or lower. Now, for Vanessa’s card to be the highest, it also needs to be higher than Thomas’. But now, there are only 11 possibilities for Thomas’ card, since Vanessa and John’s cards are already defined by our hypotheses. Out of these 11 cards, 7 are lower than Vanessa’s. Thus, assuming that Vanessa’s card is higher than John’s, the probability that her card is also higher than John’s is 7/11.

Overall, the probability that Vanessa’s card is the highest is the product of the probability that her card is higher than John’s and the probability that her card is higher than Thomas’ with regard to the fact that her card is higher than John’s. This yields (8/12)x(7/11) ≈ 0.42. This means that the probability of her having the highest card is lower than a half.

This reasoning is summed up in the following formula, where the vertical bar has to be read “knowing that“. If you don’t like formulas, don’t worry it’s the only formula of this article!

the probability of her card being higher than John’s multiplied by the probability that her card is higher than Thomas’, knowing that her card is higher than John’s. This is a very useful formula in probability, and is also the cause of many mistakes when dealing with probabilities. That’s why I really wanted to show it. Let’s now get back to the fun stuffs.

Yes! This is her best action!

You should do the same reasoning for them, that’s good exercise!

Yes?

Exactly! Thus, John’s probability of having the highest card is (11/12)x(10/11) ≈ 0.83.

Yes. Thomas’ probability of having the highest card is (9/12)x(8/11) ≈ 0.55. So he should bet yes too… So, to recapitulate, here are the players’ bets:

As it turns out, while Vanessa and John would have won one point, Thomas would have lost one.

Exactly. What you’re describing is the major concept of strategies. A strategy consists in choosing an action depending on one’s type. Mathematically, we call this a function mapping types with actions. The following figure displays the optimal strategy.

By the way, if Thomas Bayes played this game, he’d probably be quite bored and feel his presence useless.

No! Well, maybe a little a bit… But more importantly, so far, it’s just about basic probabilities which existed before Thomas Bayes!

Sequential Highest Card Game

So let’s make the game more interesting. We’ll now assume that Vanessa will bet first out loud, followed by John, and then Thomas. This means that John can take into account Vanessa’s action to improve his decision making.

Indeed. Therefore, her best strategy remains the same. Now, let’s assume the following cards are the one dealt:

Yes. Now, let’s do John’s reasoning. Before taking his decision, he knows that Vanessa said no. And he also knows that she says no if and only if she has a card lower or equal to 9. His card is 8, thus, Vanessa’s card is either a card between 1 and 7 or card 9. Out of these 8 cards, 7 of these cards are lower than his, thus, the probability that Vanessa’s card is lower than his is 7/8. Now, assuming that Vanessa’s card is lower than John’s, there are 6 cards lower than John’s left, out of 11 cards. This implies that the probability that Thomas’ card is lower than John’s is 6/11. Overall, the probability that John’s card is the highest is (7/8)x(6/11) ≈ 0.48.

Indeed! Let’s move on to Thomas now. He knows that both Vanessa and John said no. Since Vanessa said no, Thomas knows that her card is 9 or lower. Since Thomas has 9, he knows that, for sure, Vanessa’s card is lower than his. Now, John also said no. But if John had 10 or higher, he would have said yes. Thus, Thomas knows that John too has lower than 9. Thus, he knows for a fact (well, assuming that both John and Vanessa plays smartly), that he has the highest card. Thus, he’ll say yes with absolute confidence:

In the updating of beliefs with information received during the game. In our case, because the probabilities before having any information were extremely simple, we haven’t had to go through the difficulty of updating beliefs. In a more general case, this is done with Bayes’ theorem. Daniel Negreanu does a similar updating of beliefs in the following hand:

Do not forget about updating beliefs. If you do, you may end up with apparent paradox such as the Monty Hall problem, explained on AsapSCIENCE.

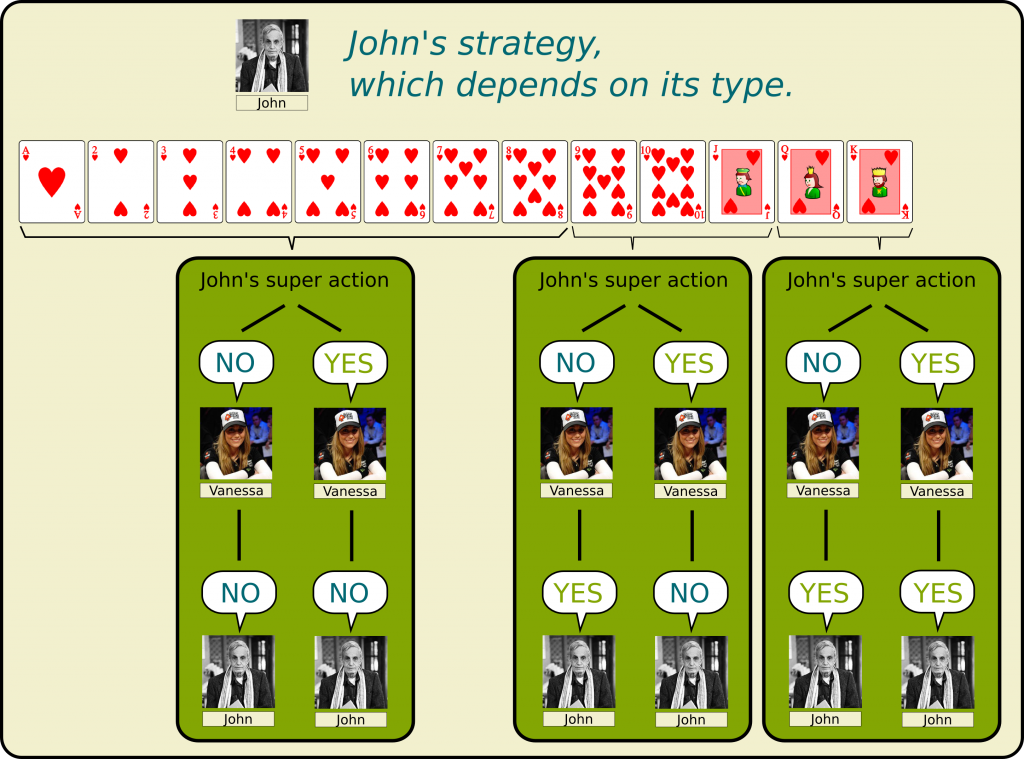
Well, they are a little bit more complicated, as the best action now also depends on the bets made so far. Now, to be consistent with the concept of strategy we have introduced earlier, let’s introduce the concept of super action. It corresponds to the way a player chooses his bet given the knowledge of the bets made so far. In other words, a super action is a reaction to information obtained during the game. Now, a strategy corresponds to a mapping of a type with a super action.

Let me rephrase. Given a player’s type, he chooses a way to react to the bets made before him. This choice of a super action depending on a type is a strategy! Let me illustrate this by displaying John’s optimal strategy:

It may seem pointless here, but this will be tremendously important in the next section.

By the way, if John Nash read my article, he’d probably be pretty mad at me so far.

I’m not sure this is what’s most important to him! The reason why he wouldn’t appreciate this article until now is that what I described isn’t really a game! Well, at least in the mathematical sense!

In this highest card game, there is no actual bilateral interaction between players. This makes things not fun enough! Well, at least for John…

Bayesian-Nash Equilibrium

Now, I could modify the game to make Vanessa’s best strategy also depend on the other players’ strategies, like for instance, allowing her to double the bets after having heard all other players’ bets. However, this would make the game very hard to understand. So, instead, I’m going to bet on your understanding of the concepts we’ve introduced so far to be more abstract.

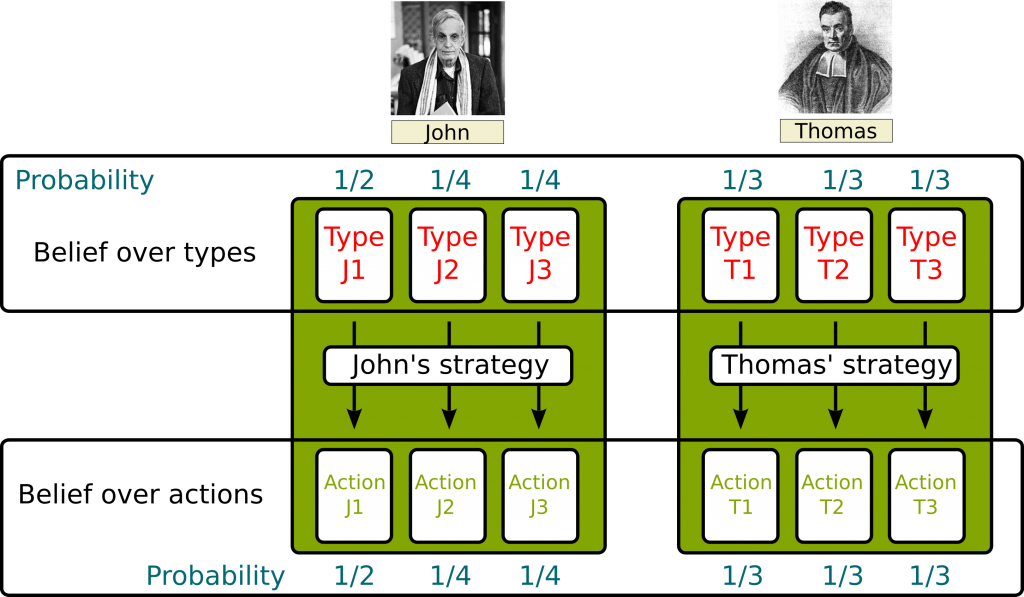
Sure. Players all have different private types. A vector of types, that is, a list of types for all players, is called a type profile. Players have a belief about the other players’ types. They are asked to play an action (or what I called super action). Similarly to type profile, we define the action profile. The way they associate their types with their actions is called the strategy. Once again, we define the strategy profile.

Good. Because we’re getting to the fundamental concept of Bayesian-Nash equilibrium.

First, let’s consider a player’s reasoning, say Vanessa’s, provided she knows the other players’ strategies. Since she has a belief about their types, she can compute the belief about their actions, as displayed in the following figure:

Since she now knows the belief about other players’ actions, she can compute, for any of her types, her best-response action to the belief over other players’ actions. If she does this for all of her possible types, she will be defining her best strategy against other players’ strategies. This is called the best-response strategy.

More mathematically, the best-response strategy is a strategy that maximizes her gain, given the belief over other players’ actions.

Something like this. A Bayesian-Nash equilibrium is a strategy profile, such that, for each player, his strategy in the strategy profile is the best-response to the other players playing the strategies of the strategy profile. Equivalently, assuming the other players will play according to the strategy profile, every player should play the strategy profile. This is displayed in the following figure:

I haven’t written it on the picture, but, obviously, not only Vanessa but also John and Thomas need to have the same reasoning for the strategy profile to be a Bayesian-Nash Equilibrium. Now, if you perfectly understand the two last figures, then, congratulation, you have mastered the concepts of Bayesian games!

Let’s Conclude

Bayesian games are disturbing at first because we need to use a probabilistic reasoning to understand them. But once we manage to think in terms of strategies instead of actions (or super actions), they can be considered conceptually without too much difficulty. However, to consider them computationally is quite difficult. This is something I have tackled in my PhD (I have submitted a research paper on this very topic, which I will put in the bibliography once it will be published).

All along this article, we have considered types which are private information with a fairly simple and computable probabilistic distribution. However, in plenty of models including the ones I use, types may include private information for which it may be very hard to obtain a good belief of. For instance, in market competition, the marginal costs of rivals are types for which the probabilistic distribution is hard to guess. This creates another big difficulty of Bayesian games.

Finally, I’ll conclude by linking Bayesian games with my PhD research. I’m studying mechanism design, in which a mechanism designer needs to define a Bayesian game to be played by agents. The mechanism designer is particularly interested in defining games for which truthfulness is a Bayesian-Nash equilibrium. As soon as my research paper gets published, I’ll get to tell you more about this…