Mathematics is often presented as the one human endeavour whose claims are indisputable. Yet, when, in the late 19th century, the giant Georg Cantor would dare to theorize mathematically about the infinite, not only would he initiate everlasting debates with the Church and philosophers, but he’d also undergo brutal objections by fellow mathematicians.
Cantor was particularly maltreated by Kronecker, who would describe him as a “scientific charlatan“, a “renegade” and a “corrupter of youth.” In fact, in his (sane) lifetime, Cantor would find hardly any supporter. Instead, the greatest mathematicians of his time would look down on him. They wouldn’t hesitate to bring him down. The doors of of the greatest mathematical institutes would be closed to him. Cantor was unwelcome. Alone against the whole mathematical community, he would feel isolated to the point of doubting his own ideas. In the end, it is not so surprising that the great genius eventually went a bit crazy.
Cantor did not have many fans. But he did have a few. In particular, fortunately for Cantor, one of the fans was the most charismatic mathematician of that time, the great David Hilbert. Hilbert viewed Cantor’s achievements as of the greatest order.
At last, Cantor’s theory that was being a rejected by the whole mathematical community would be brandished by its leader.
Today, some serious mathematicians like Norman Wildberger still refute Cantor, while others like Andrej Bauer invite us to disregard Cantor’s theory (at least every now and then). But overall, the mathematical community celebrates it as one of mankind’s greatest achievements. Cantor’s ideas are now taught in all the universities in the world as some of the most beautiful truths in mathematicss.
Hehe… Among other things, Cantor would prove that there were different infinities, with some infinities that are bigger than others…
Hilbert’s Hotel
A quick way to get a feeling of the vertigo of Cantor’s theory of the infinite is to follow the footsteps of David Hilbert. To give an insight into Cantor’s theory, Hilbert proposed a clever thought experiment. Imagine a hotel with an infinite number of rooms.
I mean a hotel with a room numbered 1, a room numbered 2, a room numbered 3… and so on to infinity.
Now, imagine that the hotel is full, and that a newcomer arrives at the desk office. Could the hotel manager, say Hilbert himself, find a room for the newcomer?
Are you sure? If the hotel was finite, your answer would be perfectly right. But don’t forget. Hilbert’s hotel is infinite.
Take your time. You can figure this one out!
Okay, here’s the trick. Hilbert could ask every guest to move to the room next to his, hence shifting all the guests by one unit. Every guest would still be having a room. But amazingly, they would also have freed the first room! There’s room for the newcomer!
I know! Think about what has just happened. We’ve shown that an infinite hotel can always accommodate a newcomer, even when it is full! Mathematically, by adding one to all guests’ rooms, we’ve also shown that there are as many whole numbers as there are whole numbers larger or equal to 2! If you’ve never heard about that, it should blow your mind!
And yet, we’re merely at the beginning of our journey in the world of the infinites! Let’s go further. Let’s now imagine that there is an infinite number of newcomers. Could Hilbert accommodate them all?
I guess… But that would take an infinite amount of time. Can Hilbert free an infinite number of room at once?
Yes. That’s what we’ve done.
You’re onto something!
Do you see the pattern?
Awesome! Thereby, we’re freeing all the odd-numbered rooms!
Amazingly, we’ve freed an infinite number of room at once! Through this doubling rule, we’ve shown that we can fit the set of whole numbers into the set of even numbers. This is astounding! It’s what’s brilliantly explain in this video by the Open University Youtube channel:
You haven’t answered my question though. Can Hilbert fit an infinite number of newcomers in his full hotel?
Obviously?
Don’t you see where you got it wrong?
You did. You assumed that the newcomers could be listed!
As astounding as it sounds, Cantor would prove that no. Some sets aren’t listable.
Listable Infinity
Let’s start with listable infinities. The most obviously listable of these infinities is evidently the whole numbers. Let me write that as a theorem with a proof.
That wasn’t hard, was it?
Now, what about positive and negative integers?
What could be the first element of this list of integers? What could the second? The third? The one after that?
Very good! Let me present that as a beautiful theorem:
Now that we have seen two examples of infinite listable sets, I can get to Cantor’s big idea. As I said in the introduction, Cantor would prove that some infinities are bigger than other infinities. But what could he mean by that?
But what does that mean? By far, Cantor’s greatest idea was to give a meaning to the “size” of a (possibly infinite) set. To understand Cantor’s insight, let’s play a game. In the following picture, are there more apples than bananas?
How do you know? Did you count them? How many of each are there?
I know. But then, how do you know that there are as many apples as bananas?
That’s not a good mathematical answer! Let me help you make it clearer…
Do you see it now?
Now this is a brilliant insight. To guarantee the fact that two sets have the same size, you don’t need to count their elements. You just need to pair up their elements. In fact, this is how Georg Cantor decided to define what it meant for two sets to have the same size. And that, my friends, is Cantor’s greatest idea!
As we’ve seen, it’s obviously a good definition when sets are finite. But interestingly, it can be applied to infinite sets too! Without this insight, there would be no Cantorian theory, no set theory, no basic foundational mathematics… we’d be back to the dark ages! OK, I might be exaggerating a little bit, but, seriously, Cantor’s definition is undeniably a major breakthrough that would inspire later mathematicians to take on the extremely fruitful abstraction of mathematical concepts.
Suppose you can list an infinite set of apples and an infinite set of bananas. Do you see a way to pair up apples and bananas?
Exactly! In fact, we have the following wonderful theorem.
By combining the three theorems we have seen, we can now assert one troubling fact. There are as many whole numbers as integers!
Now, let’s move on to a bigger test. You do know about rational numbers, don’t you?
Exactly! Can you list the rational numbers?
I know! As a matter of fact, between any two rational numbers, you can always find another rational numbers. In fact, you can find infinitely many rational numbers between any two rational numbers. So there seems to be a lot of rationals.
Are you sure?
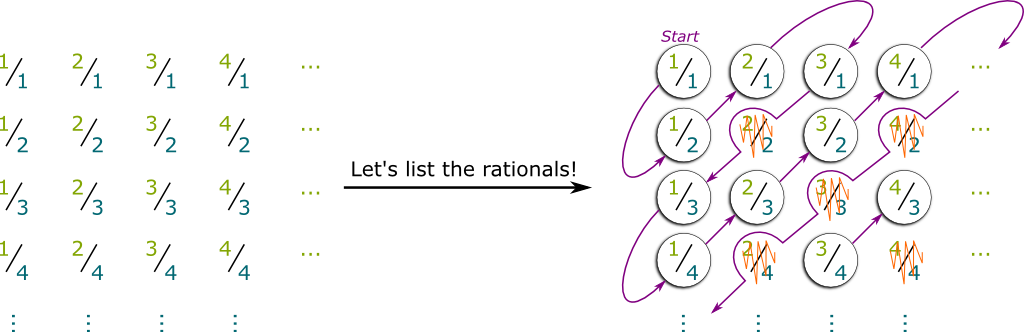
Hehe… They can! To do so, let’s first represent them in an array accordingly to the numerators and denominators:
Now, here’s the big idea. We can list the rationals by going through the down-left-to-up-right diagonals, from the inside to the outside, as we jump over the rationals we’ve already gone through. Thereby, we have a list of all positive rationals.
Now, what I’ve presented here is the classical proof that rationals are listable. But I want to tell you about a more elegant proof. In fact, you know what? I’ll let the great Matt Parker tell it to you, on Numberphile:
Unlistable Infinity
At this point, you might think that all infinities are listable…
Okay. Fair enough. So then, let’s talk about unlistable infinities. Can you think of an infinite set so big that it cannot be listed?
Let me give it to you! After all, it’s a very, very difficult question. I claim that the decimal numbers — mathematically badly named the “real” numbers — cannot be listed.
They are numbers with an infinite number of decimals. You know? Like $e \approx 2.71828182846…$ or $\tau \approx 6.28318530718…$
That’s what I’m saying. Any list of the reals would miss out on many of the reals.
The proof of it is one of the most beautiful proof of mathematics! As you’ve guessed, Cantor is the one who came up with this. His proof is a classic example of a proof by contradiction. Suppose there is a list of reals. Cantor will find something wrong about this list. Namely, he will construct a real number that is not in the list.
To determine a real number that’s not in the list, Cantor first constructed a real number whose $n^{th}$ decimal digit is the $n^{th}$ decimal digit of the $n^{th}$ number of the list. Then, he made up another real number by changing all the digits. This is the number that Cantor claims not to be in the list.
Could Cantor’s number be the $n^{th}$ element of the list?
If it were, then all the digits of Cantor’s number would be the same as the digits of the $n^{th}$ element of the list. Yet, we know by construction that Cantor’s number’s $n^{th}$ decimal digit is not the $n^{th}$ decimal digit of the $n^{th}$ number of the list!
I know! Let’s listen to Henry Reich who summed up this wonderful piece of mathematics on Minute Physics:
I can finally state this as a theorem:
In effect, this says that the infinite of real numbers is bigger than the listable infinite!
There are!
For any infinite set $E$ (like for instance, the set of real numbers), Cantor devised a clever method to construct a bigger infinity $\mathcal P(E)$, called the power set.
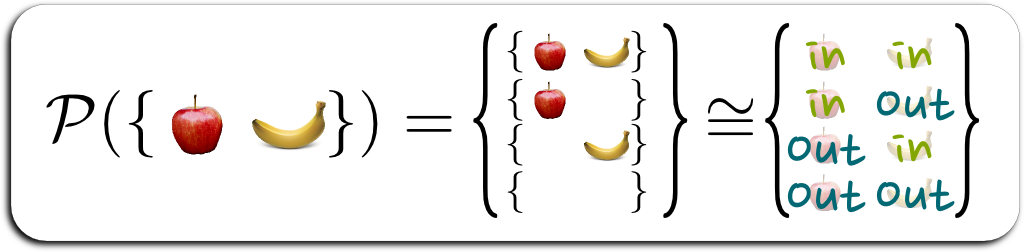
He defined $\mathcal P(E)$ as the set of subsets of $E$.
A subset of $E$ is a set that contains some but not necessarily all elements of $E$. For instance, if $E$ is a set containing an apple and a banana, $E$ has four subsets. One contains both the apple and the banana, another contains only the apple, another contains only the banana, and the last subset contains nothing. More generally, when $E$ has two elements, $\mathcal P(E)$ has four elements.
Here’s an equivalent perhaps simpler way to visualize the power set of $E$. A subset $E$ can be determined by saying for all elements $e$ of $E$ whether $e$ is in or out the subset. So, back to our apple-and-banana example, a subset is determined by whether the apple is in or out, and whether the banana is in or out. Since there are two possibilities for each element of $E$, there are globally $2^E$ possibilities. That’s why the power set $\mathcal P(E)$ is sometimes denoted $\mathcal P(E) = 2^E$.
Finally, I can state Cantor’s theorem. Cantor proved that the power set $\mathcal P(E)$ is always bigger than the set $E$. In other words, you cannot pair up elements of $E$ and of $\mathcal P(E)$.
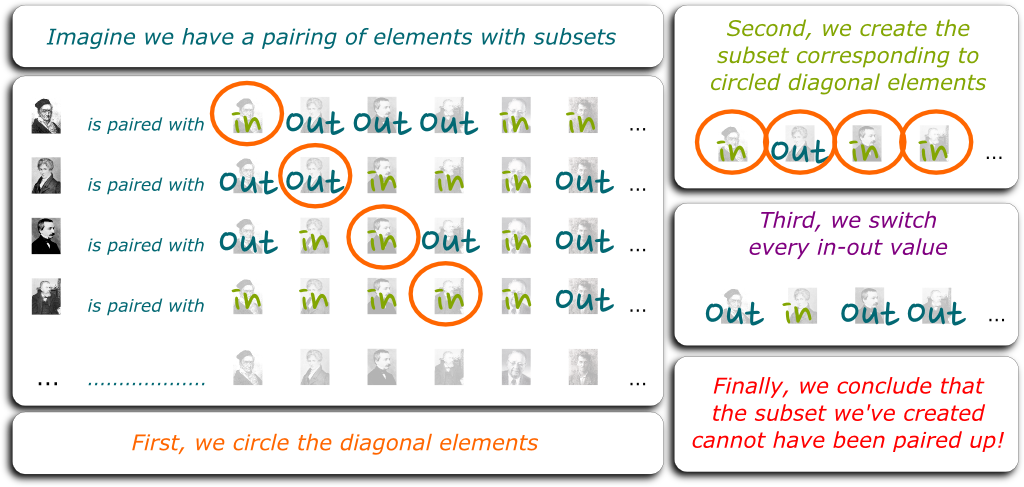
The idea of the proof is essentially the same as the proof that reals are not listable. To get the intuition of the proof, let me list elements of $E$ anyways, assume that they are paired with subsets of $E$ and write whether the subset they are paired with leave elements of $E$ in or out…
Next, like before, we are going to make up a first subset using diagonal terms, and then another subset by switching every in-or-out value. Finally, we obtain a set that could not have been paired up, because of the diagonal argument!
Do you realize what this means? It means that the power set $\mathcal P(\mathbb R)$ of the set of real numbers is strictly bigger than the set $\mathbb R$ of real numbers. More generally, there is no biggest infinity. Just take the power set of an infinite set to make up a bigger one!
The Continuum Hypothesis
Many of Cantor’s proofs are the kinds of enlightening beautiful insights that every mathematician wishes he could stumble upon by himself. But there’s one problem that defied even the great Cantor.
Hilbert found that problem so important that he put it at the top of his list of problems to be solved, when he presented a list of 23 open problems in his legendary 1900 talk. These problems would be guiding mathematicians all along the 20th century, and, surely enough, they would yield deep insights into the nature of mathematics. In fact, the one that allowed for the greatest insights might well be the first of these problems, the problem that Cantor could not solve.
It is called the continuum hypothesis. It asserts that the infinite of the reals is the smallest infinite bigger than the listable infinite. Cantor and Hilbert could not prove it.
To this day, no one has been able to prove nor disprove the continuum hypothesis.
Actually, the problem is considered solved!
It’s one of the most dramatic result in the History of mathematics! In 1940, Kurt Gödel would prove that you couldn’t prove the existence of an infinite in-between the infinites of the whole numbers and the reals. In other words, according to Gödel, the continuum hypothesis has no disproof.
Read carefully. Gödel didn’t prove that the continuum hypothesis is true. He proved that you couldn’t prove that it was false.
He did not. But in 1963, Paul Cohen would complete Gödel’s answer in the most stunning possible way. He would prove that there is no proof that the continuum hypothesis is true!
Astoundingly, Gödel and Cohen proved that no one will ever figure out the continuum hypothesis. It cannot be proved, nor can it be disproved!
This sort of unprovability had been predicted decades earlier by Kurt Gödel himself, in 1931. It’s called the (first) incompleteness theorem, which asserts that in all mathematical systems, you will always stumble upon assertions that can never be proved nor disproved. But this was a theoretical prediction that didn’t seem to come up in practice. To everyone’s surprise, it did. And not to any problem. It popped up for Hilbert’s most prestigious problem, the continuum hypothesis!
This means that you can assume that the continuum hypothesis is true, and do one kind of mathematics. But you can just as well assume that it is false, and do another kind of mathematics. These two alternatives would yield two different mathematical universes.
Exactly! Especially nowadays, many, many different universes of mathematics have been unveiled. As Andrej Bauer argues, too often though, mathematicians are stuck in their own little universe called ZFC (well, it’s actually not so small since it contains more infinites than any infinite…). ZFC is nothing less than the universe Cantor was exploring, even though he himself could not formalize it. It is also the universe that is brutally taught to students as the only evident mathematical universe one can (or should) work with.
Yes indeed! Granted, ZFC is Historically the universe mathematicians have mostly worked with. But, as Bauer argues, it’s definitely not the only interesting universe. And the cool thing about the mathematical multiverse is that it is physically possible to explore it — physics never was and never will be a limitation to mathematics! Thus, Bauer invites mathematicians to take a trip towards other universes and discover some of the unusual, but probably useful, properties of the mathematical objects they’ll encounter!

Let’s Conclude
To conclude, let me recap the listable set of amazing things we’ve uncovered about the infinites. In fact, you know what? I’m feeling a bit lazy, so I’ll just let the awesome Dennis Wildfogel sum up our findings in this wonderful Ted Education video.
Sadly, the space of this article is way too restricted to give you a full story about the infinite — to do so, I’d probably rather need an infinite amount of space! But luckily, Vi Hart gave a wonderful overview of the multitude of infinites that are extremely useful in mathematics. As you’ll see, the infinite is not always about how big it is, but rather, about how well it completes our mathematical objects.








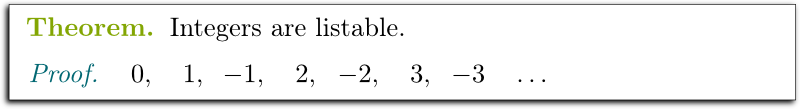



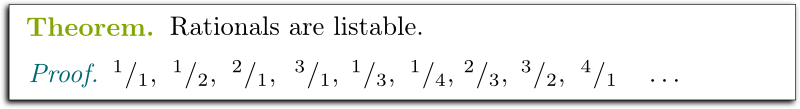



Leave a Reply