On May 31, 1832, a French Republican revolutionary called Évariste Galois died from a gunshot. He was 20 years old. The night before, fearing his own death, Galois had written many letters, frenetically scribbling “I have no time; I have no time“. One letter is particularly precious for Historical reasons. In this letter, Galois claims to have actually triggered the revolution. Not a political one. But a mathematical one.
The revolution Galois initiated turned out to be bigger and more profound than he could have possibly envisioned it! The landscape of mathematics has been deeply affected by Galois’ vision, as its progeny has risen and taken over the mathematical world. This progeny is now omnipresent and rules unbounded lands. It goes under the name of pure algebra.
To romanticize even a bit more the story-telling of Galois’ dramatic life, here’s an abstract of a documentary I made about algebra:
He definitely is! But his mathematical revolution didn’t go smoothly. Like all revolution leader, he first had the utmost difficulties. Not to envision the revolution. But to convince others to join him in a game-changing approach to mathematics. When Galois was still alive, his revolutionary ideas got rejected several times by the French science academy… Because the best French mathematicians of that time like Siméon Denis Poisson just couldn’t get it! Partly because of Galois’ unreadable handwriting displayed on the right…
In 1843, 10 years after Galois’ death, finally, a brilliant French mathematician named Joseph Liouville managed to grasp some of Galois’ ideas. After 3 more years of work, Liouville published an article to explain them. But Liouville’s article was still too far-fetched for other mathematicians to enjoy and understand. It took another 24 years to find a French mathematician outstanding enough to better understand Galois and make his ideas limpid. This outstanding mathematician is Camille Jordan. In fact, Jordan’s 1870 book on Galois theory was so well-written that German mathematician Felix Klein found it as readable as a German book!
It was definitely a huge boost. But it would take another 82 years for the great Austrian mathematician Emil Artin to finally give the Galois theory its modern form, in 1942. Artin deserves a lot of credits. While Galois was the visionary who foresaw this revolution, Artin, in many senses, is the one who actually undertook the revolution and overturned mathematics. Thanks to Artin, and a few others, today, the Galois theory has become an unavoidable cornerstone of research in mathematics, with plenty of surprising and amazing achievements (like Wiles’ proof of Fermat’s last theorem), as well as a huge reservoir of open questions and mysteries!
Fields in Pure Algebra
Galois theory is about symmetries of numbers. But before getting there, I need to introduce to get you armed by letting you on a secret about numbers. And I’m sure you’ve heard of it! Indeed, back in high school, you were probably taught never to leave roots in the denominators.
I mean that $1/(\sqrt{2}-1)$ was not a right answer. Can you help get rid of the square root of 2 in the denominator?
Hehe… We were taught to multiply up and down by the conjugate of the denominator. This conjugate is obtained by replacing $-$ by $+$ (or vice-versa) in the denominator:
I know! The complicated expression $1/(\sqrt{2}-1)$ represents the same number as $\sqrt{2}+1$. And this explains why our teachers wanted us to write results in one way rather than the other: When everything is written in the same way, exams get much easier to correct!
But what about $1/(\sqrt[3]{2}-1)$? Can you get rid of the root in the denominator? Can it even be done?
I know!
You tell me!
Any luck?
Hehe… Interestingly, any power of $\sqrt[3]{2}-1$ can be written as a sum of powers of $\sqrt[3]{2}$. Indeed, you just need to distribute the products:
Yes it is! By doing this substitution in the third equation, we have shown that the three first powers of $\sqrt[3]{2}-1$ can be written as a sum of a rational number, of $\sqrt[3]{2}$ and of $\sqrt[3]{2}^2$!
So we now have 3 equations, with 2 root expressions we want to get rid off! Thus, we can combine the equations to remove all root expressions on the right!
Let’s multiply the 2 first lines by 3 and add up all 3 equations:
Hehe… The cool thing is that the left term we’ve obtained can now be factorized by $\sqrt[3]{2}-1$! Let me skip some boring calculations… And get to the result $(\sqrt[3]{2}-1)$ $(\sqrt[3]{2}^2 + \sqrt[3]{2} + 1)$ $= 1$. So, to get rid of the roots in the denominator, we can multiply up and down by $\sqrt[3]{2}^2 + \sqrt[3]{2} + 1$! Finally, we get the following surprising and beautiful formula:
I know! But what’s even neater is that the method we used is very general! With similar technics, we can now remove all radicals from denominators!
Now, what was of particular interest to Galois wasn’t the fact that a method enabled to remove radicals from denominators. But rather, that any number with radicals in denominators equaled a number with radicals on top. This meant that the numbers with radicals on top were stable by division.
It’s common to denote $\mathbb Q[\sqrt[3]{2}]$ the set of numbers which can be written as a sum of powers of $\sqrt[3]{2}$. Since $\sqrt[3]{2}^3 = 2$ is a rational number, any sum of powers of $\sqrt[3]{2}$ can in fact be written in the standard form $a\sqrt[3]{2}^2 + b\sqrt[3]{2} + c$. Now, if you add, subtract or multiply any two such numbers, then it’s not to hard to see that we obtain numbers which can still be put in the standard form $a\sqrt[3]{2}^2 + b\sqrt[3]{2} + c$. Plus, what we have just shown here is that the inverse of all numbers $a\sqrt[3]{2}^2 + b\sqrt[3]{2} + c$ can also be written in standard form. This shows that any addition, subtraction, multiplication and division of numbers in $\mathbb Q[\sqrt[3]{2}]$ yields a number, which can be written in standard form… and thus belongs to $\mathbb Q[\sqrt[3]{2}]$. In pure algebra terms, $\mathbb Q[\sqrt[3]{2}]$ is thus stable by the four classical arithmetic operations. For this reason, we call it a field.
Geometry of Field Extensions
The field you are the most familiar with is probably the set $\mathbb Q$ of rational numbers. Other examples of fields are the sets $\mathbb R$ of real numbers and the set $\mathbb C$ of complex numbers. And now, we also have $\mathbb Q[\sqrt[3]{2}]$. Since $\mathbb Q[\sqrt[3]{2}]$ is a field which contains the field $\mathbb Q$, we say that $\mathbb Q[\sqrt[3]{2}] / \mathbb Q$ is a field extension.
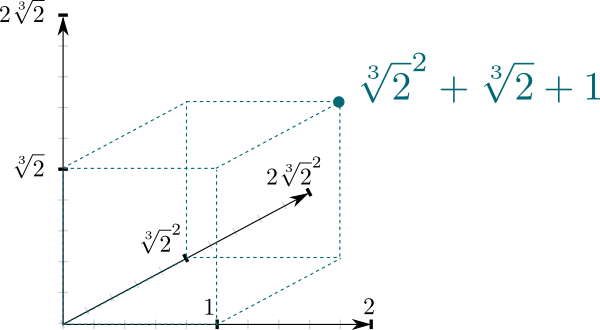
The fact that $\mathbb Q[\sqrt[3]{2}] / \mathbb Q$ is a field extension yields a very natural connection between the two fields. Namely, $\mathbb Q[\sqrt[3]{2}]$ can be seen as a vector space, where $\mathbb Q$ is the scalar field. In particular, the fact that any number in $\mathbb Q[\sqrt[3]{2}]$ can be written $a \sqrt[3]{2}^2 + b\sqrt[3]{2} + c$ means that $(1, \sqrt[3]{2}, \sqrt[3]{2}^2)$ forms a basis of $\mathbb Q[\sqrt[3]{2}]$ as a $\mathbb Q$-vector space. And this means that we can represent it geometrically as a 3-dimension space!
The dimension of the vector space above is an interesting property of field extensions. It’s known as the degree, and it is commonly denoted $\big[ \mathbb Q[\sqrt[3]{2}] : \mathbb Q\big] = 3$ for instance.
Yes! It’s actually pretty easy to create a field extension of this: Just add some radical number which does not belong to $\mathbb Q[\sqrt[3]{2}]$!
Yes! This would create the field $(\mathbb Q[\sqrt[3]{2}])[\sqrt{2}] = \mathbb Q[\sqrt[3]{2},\sqrt{2}]$. This fields contain all numbers which are products and sums of $\sqrt[3]{2}$ and $\sqrt{2}$. These are of the form $a\sqrt[3]{2}^2$+$b\sqrt[3]{2}+c$+$ d\sqrt[3]{2}^2\sqrt{2}$ +$ e \sqrt[3]{2} \sqrt{2} $+$ f \sqrt{2}$. Any idea of what the degree $\big[\mathbb Q[\sqrt[3]{2}, \sqrt{2}] : \mathbb Q[\sqrt[3]{2}]\big]$ is?
Yes! Indeed, we have $a\sqrt[3]{2}^2$+$b\sqrt[3]{2}$+$c $+$ d\sqrt[3]{2}^2\sqrt{2} $+$ e \sqrt[3]{2} \sqrt{2} $+$ f \sqrt{2} $=$ (a\sqrt[3]{2}^2+b\sqrt[3]{2}+c) $+ $(d\sqrt[3]{2}^2 + e \sqrt[3]{2} + f) \sqrt{2}$. Thus, any number of $\mathbb Q[\sqrt[3]{2},\sqrt{2}]$ can be written $A+B\sqrt{2}$, where $A$ and $B$ belong to $\mathbb Q[\sqrt[3]{2}]$. Thus, 2 scalars of $\mathbb Q[\sqrt[3]{2}]$ determine a number in $\mathbb Q[\sqrt[3]{2},\sqrt{2}]$. This means that the degree of the field extension $\mathbb Q[\sqrt[3]{2}, \sqrt{2}] / \mathbb Q[\sqrt[3]{2}]$ is 2. In fact, we have the Chasles relation $\big[\mathbb Q[\sqrt[3]{2}, \sqrt{2}] : \mathbb Q \big] $=$ \big[ \mathbb Q[\sqrt[3]{2}, \sqrt{2}] : \mathbb Q[\sqrt[3]{2}] \big] \big[ \mathbb Q[\sqrt[3]{2}] : \mathbb Q \big] $=$ 2 \times 3 = 6$.
It’s better than that! Any field extension of finite degree, called finite field extension, is spanned by a single numbers. For instance $\mathbb Q[\sqrt[3]{2}, \sqrt{2}] $=$ \mathbb Q[\sqrt[3]{2} + \sqrt{2}]$, which means that all numbers which are sums of powers of $\sqrt[3]{2}$ and $\sqrt{2}$ are also sums of powers of $\sqrt[3]{2} + \sqrt{2}$. Isn’t it surprisingly awesome?
More generally, any finite field extension of $\mathbb Q$ can be written $\mathbb Q[x]$ with some $x$ which is added to $\mathbb Q$.
Yes. It’s the case for the field extension $\mathbb R/\mathbb Q$. And, so is the most important field extension in Galois theory! This field extension is $\bar{\mathbb Q} /\mathbb Q$, where $\bar{\mathbb Q}$ is the set of algebraic numbers. These are all solutions to polynomial equations of the form $a_n x^n $+$ a_{n-1} x^{n-1} $+$ … $+$ a_1 x $+$ a_0 = 0$. For instance, $\sqrt[3]{2}$ is an algebraic number because it is solution to $x^4 – 2x = 0$. Thus, $\bar{\mathbb Q}$ is a field extension to all finite field extensions of $\mathbb Q$.
Conjugate Numbers
We’re almost there! We need a final detour through polynomial equations.
Exactly! Galois noticed that some equations could be simplified. For instance, $x^4-2x=0$ can be factorized as $x(x^3-2)=0$, which corresponds to $x=0$ or $x^3-2=0$. So, the equation $x^4-2x=0$ can be reduced to equations $x=0$ and $x^3-2=0$. And in fact, this reduction is very similar to how numbers like 35 can be reduced to 5 and 7, because $5 \times 7 = 35$. The similarity between equations and whole numbers is so strong that we can even make Euclidean divisions of polynomials, just like you learned to do it for numbers! On the right is an example of such a division (don’t worry if you don’t understand it, it won’t be important for the sequel).
Exactly! These are known as irreducible polynomial equations. The equation $x^3-2=0$ is an example of irreducible polynomial equation.
Yes! But, crucially, Galois wanted to focus on equations with rational coefficients. Or, rather, polynomials with coefficients which belong to the base field. So, what I meant was that, for $\mathbb Q$ as the base field, $x^3-2=0$ is irreducible.
Let’s consider $x^2 – 2x -1=0$ to have some clues. This equation can be proved to be irreducible. Do you remember how to solve it?
If $b^2-4ac \geq 0$, yes.
Exactly! So, the irreducible polynomial equation $x^2 + 2x -1=0$ has two solutions: $1+\sqrt{2}$ and $1-\sqrt{2}$… Any comment?
Bingo! That’s the key discovery of Galois. More generally, Galois called conjugates all the solutions to an irreducible polynomial equation. And, as you can imagine, these are essential to remove radicals from denominators!
The first thing to notice is that if $x_1$, $x_2$, …, $x_n$ are all the solutions of a polynomial irreducible equation $a_n x^n + a_{n-1} x^{n-1} $+$ … + a_1 x + a_0 = 0$ with rational coefficients, then this polynomial irreducible equation can actually be rewritten $a_n(x-x_1)(x-x_2)…(x-x_n)=0$. Identifying the constant terms then yields $x_1 x_2 … x_n $=$ (-1)^n a_0/a_n$. So, crucially, the product of conjugate numbers is the rational number $(-1)^n a_0/a_n$, which is non-zero (prove it!).
Here’s a little joke to keep in mind the strong connection between conjugates:
Consider a fraction $1/x_1$, where $x_1$ is a complicated expression with radicals. Multiplying up and down by the conjugates $x_2$, …, $x_n$ of $x_1$ then yields $1/x_1 $=$ (-1)^n a_n x_2…x_n/a_0$, which has no radical in the denominator as we’ve established $a_0$ to be a non-zero number of the base field!
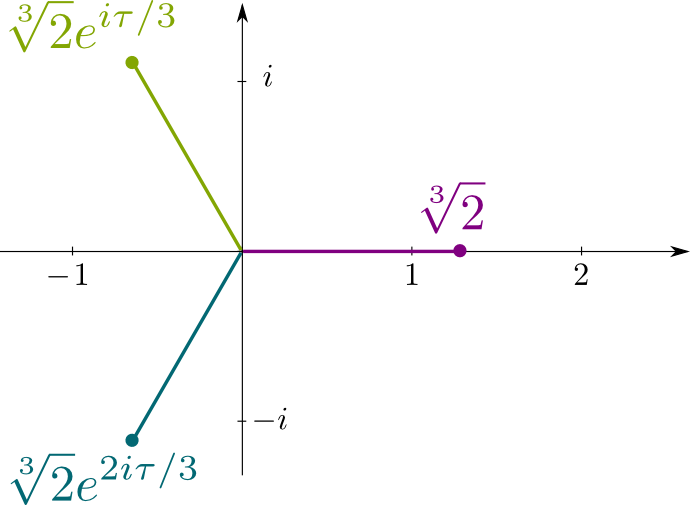
Recall that $x^3-2=0$ is the irreducible polynomial equation $\sqrt[3]{2}$ is the solution of. So, its conjugates are the other solutions to that equation, which are the complex numbers $\sqrt[3]{2}j$ and $\sqrt[3]{2}j^2$, where $j= e^{i\tau/3}$ with $\tau = 2\pi$ being the ratio of the circumference of a circle by its radius. The following figure displays the locations of the conjugate solutions in this complex plane:
Galois’ Ambiguity
Finally, we’re getting to Galois’s key insight!
Conjugates are perfectly permutable. This means that, if you systematically change $\sqrt{2}$ by its conjugate $-\sqrt{2}$, then equalities still hold. For instance, since we had $1/(\sqrt{2}-1) = \sqrt{2}+1$, I can straightforwardly tell you that $1/(-\sqrt{2}-1)=-\sqrt{2}+1$! Similarly, we have the following stunning implication:
Hehe… Let me first recall that finite fields are spanned by a single element. So, if the base field is $\mathbb Q$, any finite field can be written $\mathbb Q[x_1]$ for some right $x_1$. Now, consider $x^n + a_{n-1}x^{n-1} $+$ … + a_1 x + a_0 = 0$ the irreducible polynomial equation $x_1$ is the solution of. Then, what defines $\mathbb Q[x_1]$ is the $\mathbb Q$-vector space spanned by $x_1$, $x_1^2$, …, $x_1^{n-1}$, with the simplification of greater powers of $x_1$ accordingly to the algebraic rule $x_1^n $=$ – a_{n-1}x_1^{n-1} $-$ … – a_0$.
Exactly! Crucially, these algebraic rules of $\mathbb Q[x_1]$ do not really depend on the nature of $x_1$; they only depend on the irreducible polynomial $x_1$ is the solution of! Therefore, the rules of $\mathbb Q[x_1]$ are identical to these of $\mathbb Q[x_2]$, …, $\mathbb Q[x_n]$, where $x_1$ is replaced by one of its conjugates $x_2$, …, $x_n$. In particular, the fields $\mathbb Q[\sqrt[3]{2}]$ and $\mathbb Q[\sqrt[3]{2} j]$ operate accordingly to the exact same rules. That’s why conjugates are perfectly permutable! We say that the fields $\mathbb Q[\sqrt[3]{2}]$ and $\mathbb Q[\sqrt[3]{2} j]$ are isomorphic, and that replacing $\sqrt[3]{2}$ by $\sqrt[3]{2}j$ is an isomorphism $\mathbb Q[\sqrt[3]{2}] \rightarrow \mathbb Q[\sqrt[3]{2}j]$.
In a very similar (but stronger) way that two vector spaces of dimension 2 are more or less the same! This has a terrible consequence. It means that, from an algebraic perspective, it is meaningless to make a difference between a number and any of its conjugates (as long as you systematically replace the number by its conjugate)! So, for instance, $\sqrt{2}$ and $-\sqrt{2}$ are algebraically indistinguishable! To keep this in mind, here’s another joke I’ve come up with:
Not at all! Any distinction between these two numbers must involve some other mathematics than algebra, like order relations or topology. What I mean is that, for instance, the relation $\sqrt{2} > 0$ does make a difference between $\sqrt{2}$ by $-\sqrt{2}$, but that’s because it involves an order relation. But if we restrict ourselves to polynomial equalities, then there is absolutely no difference between $\sqrt{2}$ and $-\sqrt{2}$. Similarly, $i$ and $-i$, the solutions of the irreducible polynomial equation $x^2+1=0$, are also algebraically indistinguishable. Yet, we call arbitrarily $i$ one of them. This is why Galois called his theory the theory of ambiguity. Today, the ambiguity of the choice of the conventional square root of $-1$ among $i$ and $-i$ is rather called the symmetry between $i$ and $-i$.
Galois Groups
Galois particularly focused on field extensions which are stable by conjugacy. Such stable field extensions are now known as Galois extensions. So, if $x_1$ belongs to a Galois extension, then this Galois extension contains all its conjugates $x_2$, …, $x_n$.
A simple way to construct Galois extensions consists in taking the field spanned by solutions of an irreducible polynomial equation. For instance, if $x_1$, …, $x_n$ are conjugates for the base field $\mathbb Q$, then $\mathbb Q[x_1, …, x_n] / \mathbb Q$ is a Galois extension. Fields constructed this way are called splitting fields.
For instance, the splitting field of equation $x^3-2=0$ is the Galois extension $\mathbb Q[\sqrt[3]{2}, \sqrt[3]{2} j, \sqrt[3]{2} j^2] / \mathbb Q$ spanned by its solutions.
If $x_1$ spans a Galois extension, then so do its conjugates. Thus, $\mathbb Q[x_1] = \mathbb Q[x_2] =$ … $=\mathbb Q[x_n]$ = $\mathbb Q[x_1,…, x_n]$. Thus, the isomorphism between $\mathbb Q[x_1]$ and $\mathbb Q[x_2]$ which consists in always replacing $x_1$ by $x_2$ is in fact an isomorphism between $\mathbb Q[x_1,…,x_n]$ and itself! We call it an automorphism. Automorphisms of a Galois extension $\mathbb Q[x_1,…,x_n]/\mathbb Q$ forms the Galois group $Gal(\mathbb Q[x_1,…,x_n]/\mathbb Q)$.
Now, crucially, if $\mathbb Q[x_1] = \mathbb Q[x_1,…,x_n]$, then all automorphisms of a Galois extension $\mathbb Q[x_1,…,x_n]/ \mathbb Q$ are permutations of $x_1$ with one of its conjugates! In particular, we see here that the cardinality of a Galois group equals the degree of the Galois extension.
Sure! You can notice that $\mathbb Q[i] = \mathbb Q[i,-i]$ and $\mathbb Q[\sqrt{2}] = \mathbb Q[\sqrt{2},-\sqrt{2}]$, which means that $i$ and $\sqrt{2}$ each spans the splitting fields of the irreducible polynomial equation they are solution of. Thus, $\mathbb Q[i]/\mathbb Q$ and $\mathbb Q[\sqrt{2}]/\mathbb Q$ are both Galois extensions. Therefore, their automorphisms consist in replacing $i$ by one of its conjugates, $i$ or $-i$, and replacing $\sqrt{2}$ by $\sqrt{2}$ or $-\sqrt{2}$. In the first cases, we aren’t changing anything to numbers, which corresponds the zero symmetry. The second cases can be visualized as axial symmetries, as displayed in the figure below:
Isn’t that amazing?
Sure! Let’s get to the splitting field $\mathbb Q[\sqrt[3]{2},\sqrt[3]{2}j, \sqrt[3]{2}j^2]$ of $x^3-2=0$. But, before going any further, let’s notice that $\mathbb Q[\sqrt[3]{2},\sqrt[3]{2}j, \sqrt[3]{2}j^2] = \mathbb Q[\sqrt[3]{2}, j]$.
All we need to prove is that all generators of one field belongs to the other. Let’s start by proving that the generators of the latter, $\sqrt[3]{2}$ and $j$, belong to the former. It’s obvious for $\sqrt[3]{2}$. Now, $j = (\sqrt[3]{2} j) / \sqrt[3]{2}$, thus $j$ belong to the former field too. This proves that all elements of $\mathbb Q[\sqrt[3]{2},j]$ belong to $\mathbb Q[\sqrt[3]{2}, \sqrt[3]{2} j, \sqrt[3]{2} j^2]$. Reciprocally, it’s straightforward that all generators of the former field, $\sqrt[3]{2}$, $\sqrt[3]{2}j$ and $\sqrt[3]{2}j^2$, are products of the generators of the latter. Thus, both fields are equal. And, in particular, $\mathbb Q[\sqrt[3]{2}, j]/\mathbb Q$ is a Galois extension.
Hehe… To understand the symmetries of $\mathbb Q[\sqrt[3]{2}]$, we’ll need to go further in Galois’ study of Galois groups…
Galois Correspondence
The trouble with Galois groups is that they can become extremely large and complicated. This is particularly the case of the infinite group $Gal(\bar{\mathbb Q}/\mathbb Q)$. To apprehend such huge and complex groups, Galois had the brilliant idea to break these into smaller pieces.
Amazingly, Galois found out that Galois groups could be broken into subgroups of symmetries by only looking at those which leave some subfield unchanged. For example, $\mathbb Q[j]$ is a subfield of $\mathbb Q[\sqrt[3]{2},j]$, since any number of the former belongs to the latter. Thus, symmetries of $\mathbb Q[\sqrt[3]{2},j]$ which do not change anything to $\mathbb Q[j]$ form a subgroup of the Galois group of $\mathbb Q[\sqrt[3]{2},j]/\mathbb Q$. These symmetries form the Galois group $Gal(\mathbb Q[\sqrt[3]{2},j]/\mathbb Q[j])$.
I know! I like to visualize these symmetries as the ways to plug $\mathbb Q[\sqrt[3]{2},j]$ onto $\mathbb Q[j]$. Here’s an imaged picture of the “plugging onto“:
Exactly! And that’s simply because $\mathbb Q[\sqrt[3]{2},j]$ is a Galois extension of $\mathbb Q[j]$ which is itself a field extension of $\mathbb Q$.
And there’s more! Galois showed that all subgroups of a Galois extensions are obtained this way! More precisely, the mapping of any field $K$ in-between the Galois extension $\mathbb Q[\sqrt[3]{2},j]$ and the base field $\mathbb Q$ to the Galois group $Gal(\mathbb Q[\sqrt[3]{2},j] / K)$ is bijective. This fact is called the Galois correspondence! This correspondence is schematically displayed below for a Galois extension $\mathbb Q[x]/\mathbb Q$.
Instead of trying to describe this group directly, let’s focus on its subgroup $Gal(\mathbb Q[\sqrt[3]{2}, j]/\mathbb Q[j])$. It is straightforward that $\sqrt[3]{2}$ spans $\mathbb Q[\sqrt[3]{2},j]$ when added to $\mathbb Q[j]$. Thus, $\mathbb Q[\sqrt[3]{2},j]/\mathbb Q[j]$ is a Galois extension spanned by $\sqrt[3]{2}$. Therefore, using a theorem we have seen earlier, we know that all automorphisms of this Galois extension consist in replacing $\sqrt[3]{2}$ by one of its 3 conjugates (itself, $\sqrt[3]{2} j$ and $\sqrt[3]{2} j^2$)!
Now, I could keep on studying other pieces of $Gal(\mathbb Q[\sqrt[3]{2}, j]/\mathbb Q)$, like the Galois subgroup $Gal(\mathbb Q[\sqrt[3]{2},j]/\mathbb Q[\sqrt[3]{2}])$. But I’ll rather use another of Galois’ powerful theorems. Namely, he proved that if $\mathbb Q[j]/\mathbb Q$ was in addition a Galois extension itself, then the subgroup $Gal(\mathbb Q[\sqrt[3]{2}, j]/\mathbb Q[j])$ is normal.
Thus, the Galois group of $\mathbb Q[\sqrt[3]{2},j]/\mathbb Q$ can be quotiented by this subgroup, and the quotient group then equals $Gal(\mathbb Q[j]/\mathbb Q)$. Yet, $\mathbb Q[j]/\mathbb Q$ is indeed a Galois extension spanned by $j$, whose conjugate is $j^2$. Thus, $Gal(\mathbb Q[j]/\mathbb Q)$ consists in either leaving $j$ as $j$ or replacing it with $j^2$.
We can now deduce all symmetries of $Gal(\mathbb Q[\sqrt[3]{2},j]/\mathbb Q)$ by combining these of $Gal(\mathbb Q[\sqrt[3]{2},j] / \mathbb Q[j])$ and $Gal(\mathbb Q[j]/\mathbb Q)$. We can display these symmetries by drawing how they affect our three spanning conjugates $\sqrt[3]{2}$, $\sqrt[3]{2}j$ and $\sqrt[3]{2}j^2$:
Crucially, the figure above contains all the symmetries of $Gal(\mathbb Q[\sqrt[3]{2},j]/\mathbb Q)$. And amazingly, these symmetries correspond to well-known group of symmetry.
I’ll let Marcus du Sautoy present it to you:
So, are symmetries here like a starfish or like a triangle?
Yes, indeed! This group of symmetries of the triangle is called $D_3$, and it is the same as the group $S_3$ of permutations of 3 elements. This leads us to the following formula, which I found so beautiful, that I’ve decided to frame it!
Let’s Conclude
In many ways, Galois is to be regarded as the father of modern algebra. His key insight was to look at mathematics through the angle of the rules of operations, and this led him to unveil surprising and insightful ambiguities, or symmetries, between numbers. From an algebraic perspective, numbers like $\sqrt[3]{2}$, $\sqrt[3]{2}j$ and $\sqrt[3]{2}j^2$ are indeed perfectly symmetric and totally interchangeable.
The understanding of these symmetries has had astonishing applications in algebraic geometry and algebraic topology among others. In particular, early successes of the theory include a classification of constructible regular polygons and a theorem asserting that high degree polynomial equations could not be solved by radicals.
Recent successes appear in cryptography and Andrew Wiles’ proof of Fermat’s last theorem. This proof involves studying the Galois group $Gal(\bar{\mathbb Q} /\mathbb Q)$ with group representation. But I’d say that the theory is somehow still young, and a lot is left to discover. After all, it’s one of the most active area of research in today’s pure mathematics research.
This should lead us to pay many more tributes to Galois’ unbelievable genius… Let me include one by SocraticaStudios.


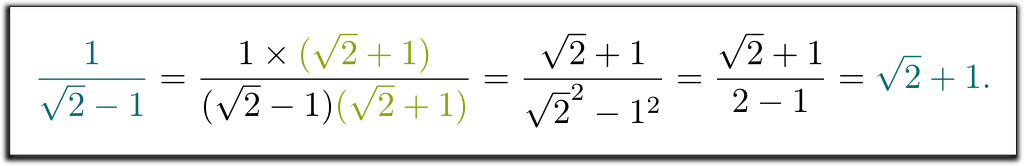
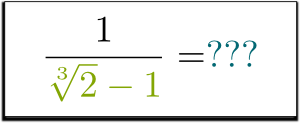
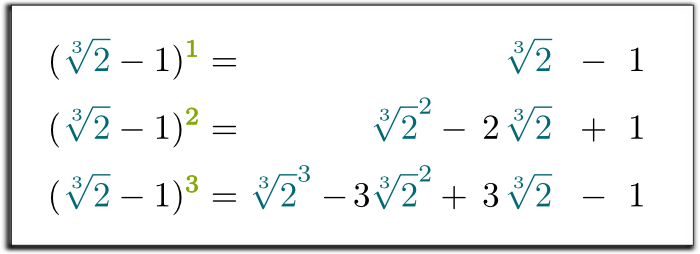
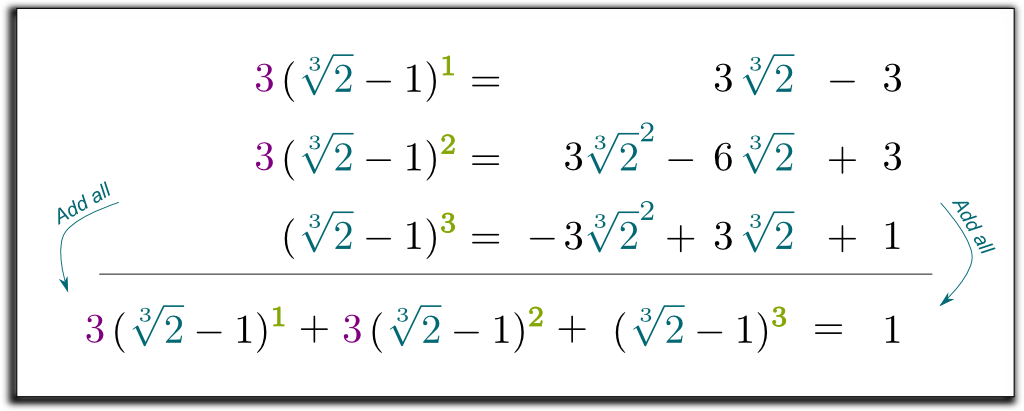
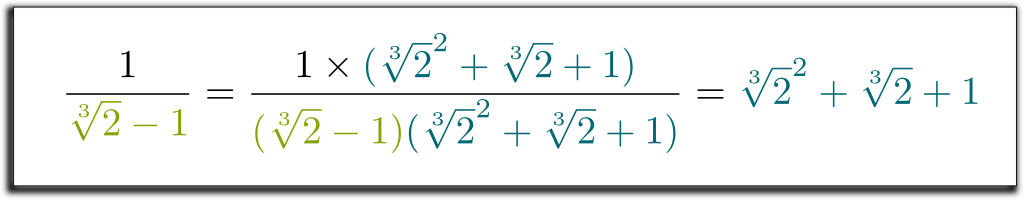
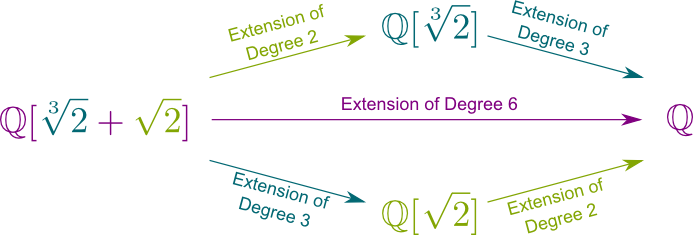


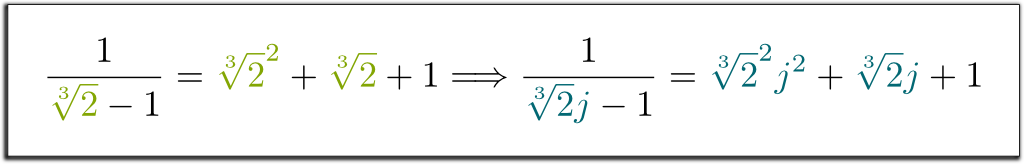


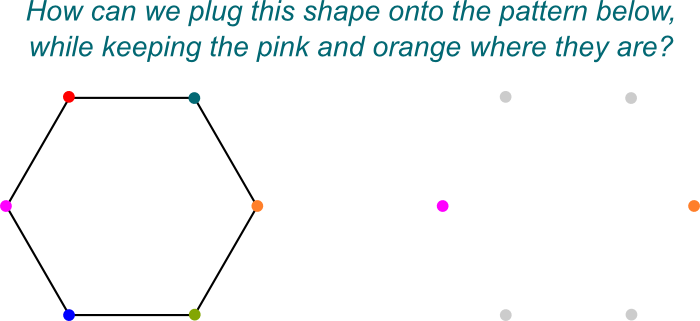

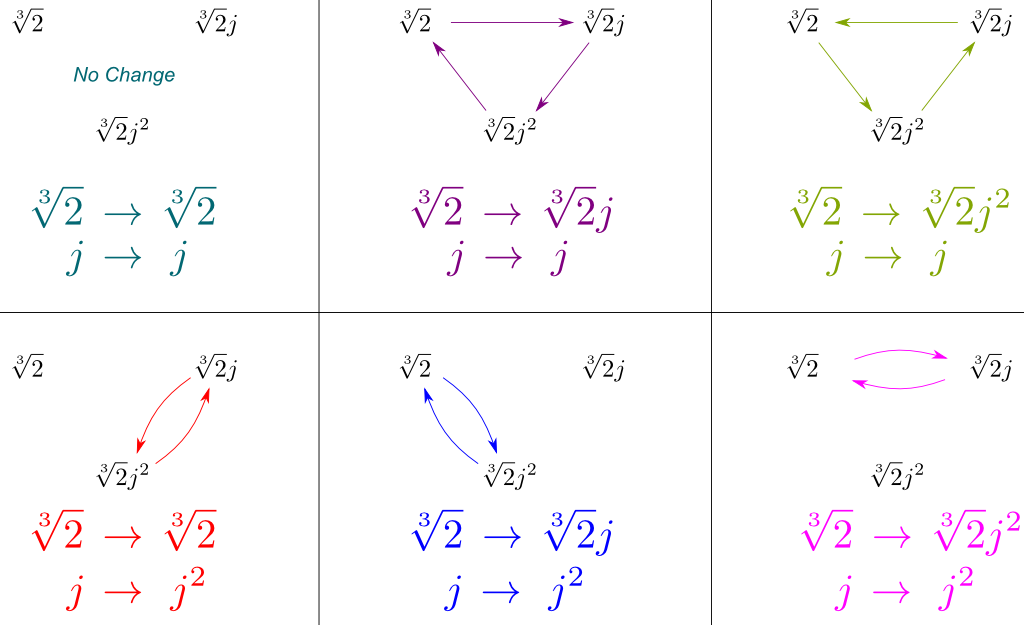
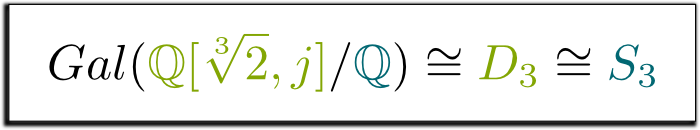
Leave a Reply