The second part of my last summer’s 2-hour video documentary has been released! If you have no idea what I’m talking about, here’s the trailer (with English subtitles):
Just like what I’ve done for the first part, I’m going to more or less recount what’s in the documentary, with several detours!
Pi
While it wasn’t the main motivation for the invention of analysis, the History of our knowledge of $\pi$ is tightly bound to the advancements of analysis. While I don’t expect you to know much about mathematical analysis, I’m assuming you know $\pi$…
Yes. Yet, despite its amazingly simple definition, $\pi$ is wonderfully ungraspable! This is because, as it turns out, $\pi$ is an entity that sort of lives outside the realm of algebra… I know I sound mysterious, but there’s a mathematical way of saying it: $\pi$ is not algebraic.
Not easily, for sure! Back in Ancient Egypt, $\pi$ was approximated by $3.16$. In Ancient Babylonia, it was approximated by $3.125$. In the Bible, it appears as $3$ (a well of diameter 1 having a circumference of 3). But the funniest (or most embarrassing) Historical approximation of $\pi$ occurred when the state of Indiana in the US, in 1897, nearly passed a law that would have enforced $\pi$ to equal $3.2$, as explained by James Grime on Numberphile:
The thing with $\pi$, is that it does not depend on our human laws. Worse, $\pi$ does not depend on any human culture. It transcends all man-made creations! Even more mind-blowing is the fact $\pi$ doesn’t even depend on our physics. This means that, for sure, any intelligent civilization, within our universe or even out of it, has stumbled upon $\pi$ (or upon $\tau = 2\pi$). More than anything else in culture, $\pi$ is universal.
I did.
This is a great question! And the answer lies in the magic of analysis. Roughly, I’d describe analysis as the art of making accurate approximations. This will require a lot of rigour, but a lot of imagination and creativity as well. And this is why I love analysis: It’s all about finding out clever ways to formalize our intuitions. Thereby, analysis sometimes confirms our intuition. But, more often than not, it allows us to reject our misconceptions. In fact, what makes analysis so appealing to me is precisely that it’s a field in which we often prove our intuitions wrong!
The first person to answer this is definitely the greatest genius of Antiquity: Archimedes of Syracuse. Not only did Archimedes find a great approximation of $\pi$, but, more importantly, he also made sure that his approximation was “accurate”. Indeed, as opposed to all others, Archimedes also proved that his approximation was the right 3-digit approximation: Archimedes wrote $\pi \approx 3.14$ (or, rather, could have written it, if he had base-10 digits…) and knew that this approximation would never be questioned.
He used a method we now call the exhaustion method. Basically, he bounded the value of $\pi$ by two sequences of numbers that both converged to $\pi$. This is what I explained in the following extract:
In addition to giving this right approximation, Archimedes was also hinting at an exact description of $\pi$: By taking his exhaustion method to infinity, Archimedes had described $\pi$ exactly!
I know. But for 2,000 years, no one could make a “better” description of $\pi$. But then came the Indian genius Madhava. As opposed to Archimedes’ highly indirect approach, Madhava found a relatively direct description of $\pi$, by using a clever and surprising trick.
Madhava wrote $\pi$ as the result of an infinite sum of simple terms! Namely, he wrote:
The more terms you add, the better you approximate $\pi$. In other words, the error of your approximation decreases and goes to zero. In modern mathematical terms, we say that the infinite series $4-^4/_3+^4/_5-^4/_7+…$ has a limit, and this limit is $\pi$.
It would. But it’s not possible. This is what I mean when I assert that $\pi$ does not belong to algebra.
Calculus
If you’re troubled by the use of infinity to describe a number like $\pi$, you’re not the only one. All along History, and even today, many great minds (like Gauss in those days or Wildberger nowadays) refused to acknowledge its existence. But, whether infinity itself exists or not, its use in calculus has turned out to be essential. To understand what I mean, I need to take you back to 17th Century Europe, when the father of modern science, Isaac Newton, made the terribly empowering proposal to introduce infinity into mathematics and physics.
If you run 10 miles in half an hour and 5 in another half an hour, then you’ll have run 15 miles in an hour. The formula $v=d/t$ then tells you that your speed was 15 miles per hour. But, for Newton, this was not satisfactory, because it’s only the average speed over an hour of running. Newton wanted a more precise description of speed. What was your exact speed twenty minutes after you started running?
Well, this datum that I gave you is actually itself an average over the first half an hour. Granted, it’s probably more accurate than the average over an hour. But Newton knew we could be more accurate — at least in principle. To do so, he shrank the time period over which the average was made. He argued that the smaller the time period, the more accurate the speed calculation. At the limit, when time periods became infinitely small, he argued that the average speed he computed was no longer an approximation. Or, rather, it was an infinitely accurate approximation.
In modern terms, we’d say that Newton was computing the variation of your position in time, technically known as the derivative. This derivative has since become ubiquitous in physics, mechanics, economics, biology, chemistry, ecology… in fact, anywhere, really. This is because, whatever we study, we want to understand how parameters of an experiment affect its outcome: Will economical growth decrease unemployment? Will malaria be extinct if we use more mosquito repellents? How will climate vary when CO2 increases? The answers to such questions are naturally framed in the language of derivatives.
If Newton got a lot of (deserved) credits for his mathematics, the German Leibniz, who first published about differential and integral calculus, did not. Newton claimed that Leibniz had stolen ideas from him. And unfortunately for Leibniz, Newton was politically well-established. Namely, he was president of the Royal Society, which was in charge of the “investigation” on the invention of calculus and… Surprise, surprise! The Royal Society decided to give full credit to Newton!
The story of this epic rivalry of the History of science is told beautifully by Audrey Brand:
In the end though, because Leibniz was friend with the Bernoullis, his mathematics and his noun were kept for posterity. In fact, today, our calculus uses Leibniz’s rigorous notations rather than like Newton’s clumsy “fluxions”.
The Bernoullis are basically the only dynasty of mathematicians, as they reigned over the mathematical world from Basel, Switzerland. They welcomed Leibniz’s calculus, perfected it and spread it all over Europe. But, perhaps even more importantly, they educated a future giant of mathematics, the great, great, Leonhard Euler…
Infinite Series
It’s hard to stress how important Euler was in the development of mathematics. Without him, we might still be discovering the steam engine…
I guess I am. But the thing with Euler is that he published so many quality memoirs that he became a reference every other mathematician could rely on. As Laplace put it, “read Euler, read Euler, he is the master of us all”. As a result, soon enough, all mathematicians started using Euler’s notations. Suddenly, everyone was talking the same language, which, assuredly, gave mathematics a huge boost!
A hundred books wouldn’t suffice to answer this question! But, in the context of this article, I want to tell you about two contributions, which both have to do with infinite series.
It’s an infinite sum, like Madhava’s.
I have no idea. Anyways, by Euler’s time, Madhava (and Leibniz) had already shown the power of series to describe many more numbers like $\pi$. Euler would take this effort much much further. For instance, he showed that the series $1+^1/_{2^2}+^1/_{3^2}+^1/_{4^2}+^1/_{5^2}+…$ was equal to $\pi^2/6$!
I know! It’s very troubling. He went on proving that $1+^1/_{2^4}+^1/_{3^4}+^1/_{4^4}+^1/_{5^4}+…$ was $\pi^4/90$!
I know. It’s so weird! But there’s even weirder! Check this numberphile video…
Playing with infinite series led Euler to derive the equality $1+2+3+4+5+… = -1/12$.
Hummm… I don’t know. Physicists have been using it, and there are many different, quite sound ways to get to this astounding equality!
More generally, he studied in length the series of the form $1+^1/_{2^s}+^1/_{3^s}+^1/_{4^s}+^1/_{5^s}+…$, where $s$ is a number like -1, 2 or 4. Amazingly, Euler proved that these series were intimately connected to prime numbers, as they equaled the product $(1-p^{-s})^{-1}$ for all primes $p$.
Don’t worry. The details here don’t matter. What’s important to notice is that the relatively simple left series is closely related to primes, because it can be rewritten as an infinite product that features the set of all primes. This remark as at the core of today’s most important open problem of mathematics. But we’ll get back to this in a bit…
For now, let’s talk about another of Euler’s many contributions. Euler noticed that many well-known complicated functions like the sine, the cosine and the exponential could be written as infinite sums of power of $x$. For instance, $exp(x) = 1+\frac{x}{1}+\frac{x^2}{1 \times 2}+ \frac{x^3}{1 \times 2 \times 3}+…$ That’s already quite remarkable (although a more rigorous proof would have to wait for Taylor and Lagrange). But Euler proved something even more surprising and beautiful.
By replacing $x$ by $it$ (where $i$ is the famous square root of $-1$), and by then playing around with infinite sums, Euler proved that the exponential was intimately connected to the sine and the cosine. Somehow, out of the black magic of abstract manipulations of infinite series, Euler found out that $exp(it)=\cos(t)+i \sin(t)$. If you don’t get it, don’t worry. Just trust me. This is truly mind-blowing.
Oh yes! I’m obliged to say that Euler also replaced $t$ by $\pi$. The equation then yields $e^{i\pi} + 1 = 0$. This is usually referred to as the most beautiful equation in the whole of mathematics. And there’s a good reason for this: It bridges all the most important numbers in the world that, prior to Euler, seemed to be totally disconnected. Plus, it does so in a very neat manner, involving exactly one addition, one multiplication and one exponentiation. Beautiful! One more reason why Euler is so awesome!
Differential Equations
Now, in truth, what makes Euler’s identity so essential is not its beauty. Rather, it’s how simply its derivative is. As you’ve probably learned it, the derivative of $e^t$ is $e^t$. In other words, the function $e^t$ is a solution to the differential equation $\dot x = x$, that requires the derivative of the function $x(t)$ be equal the function $x(t)$ itself. Even more interesting is probably the fact that the function $e^{it}$ is the solution to the differential equation $\ddot x = -x$.
And, amazingly, it’s overwhelmingly useful! Indeed, as mathematicians understood more and more Newton’s equations, the importance of such differential equations has skyrocketed. Almost literally.
First, I need to tell you about Newton’s laws. They say that the acceleration of any object depends on the forces acting on it. Yet, forces that act on a object depend on the position of the object. For instance, the closer the object is to a massive object, the more gravity will pull it. Thus, acceleration is a function of the forces, which are functions of position. In particular, the position of an object determines its acceleration. Yet, acceleration is precisely the second derivative of the position. This means that it determines the future positions of the object. So, overall, the position of an object determines its future positions. This translates mathematically into a differential equation, whose solutions describe the position of the object at all times.
Exactly! And, importantly, predicting the future can be done by simply solving such a differential equation. Today, they are widely used throughout engineering, like, for instance, in skyrocket science, but, also in more surprising areas like geopolitical predictions! And yet, the mathematical study of differential equations is often shrouded with mysteries, as well as, deep, fundamental, philosophically troubling consequences.
Before finding solutions to a (complicated) equation, mathematicians usually first wonder whether the equation even has solutions. And if it has, how many?
You’d expect your differential equation to predict some future… and, ideally, only one kind of future. The worst kind of science would be the kind that makes no prediction, or, even worse, that predicts something and its opposite!
In general, no. However, in the 19th Century, the great Augustin-Louis Cauchy, along with others (Lipschitz, Picard and Lindelöf), has proved that Newtonian dynamic differential equations did have, in general, a unique solution.
And that’s a big deal!
Cauchy’s theorem means Newton’s laws predict one and only one future.
Don’t you see? It means that our world is fully determined. It means that nothing can change the future. Not me. Not you. Not our free wills. Not even God!
Complex Analysis
Let me get back to Euler’s identity, once again. It might disturb you that physicists use it, even though it involves the imaginary number $i$. In truth, in many cases, they could solve problems without $i$. But it’d be foolish not to use Euler’s exponential $e^{it}$ because, after all, $e^{it}$ is an incredibly simple expression. It yields a geometric picture to differential equations, and, most importantly, it greatly facilitates algebraic manipulations. As weird as that may sound, imaginary and complex numbers simplify everything!
In fact, in those days, by default, “numbers” were always “complex numbers”, not “real numbers”. That’s because Gauss and Cauchy’s greatly simplified numerous fields like geographical mapping and fluid mechanics by using of these complex numbers. The details are a bit technical, but importantly, complex numbers have very enjoyable properties.
One property is that the local knowledge of a differential complex function suffices to determine it uniquely globally. It’s as if we could derive the whole American culture from the study of Montpelier, New Hampshire. It’s very startling. It’s not true for differential real functions. But, surprisingly, it is true for complex functions. And this has major implications.
Remember Euler’s series $1+^1/_{2^s}+^1/_{3^s}+^1/_{4^s}+^1/_{5^s}+…$? In the 19th Century, the great Bernhard Riemann noticed that this series, which is deeply connected to prime numbers, could be better analyzed by regarding it as a complex function. In particular, Riemann showed that this series was only revealing part of an underlying important complex function $\zeta$, now called the Riemann zeta function. By then proving that $\zeta(-1) = -^1/_{12}$, Riemann gave the first solid evidence for asserting that the infinite sum $1+2+3+4+…$ is tightly bound to the value $-^1/_{12}$. But there’s more. Following Euler’s insight, Riemann proved that the solutions of equation $\zeta(s) = 0$, called zeroes, were tightly bound to the distribution of prime numbers. And this led him to a conjecture…
I am! By experts’ accounts, the Riemann hypothesis is today’s most important and prestigious open problem. The greatest mathematicians since Riemann, including Hardy, Turing and Cohen, have given up their souls (sometimes almost literally) in the hope of cracking it. As many modern mathematicians put it, anyone who solves the Riemann hypothesis will forever be remembered as the like of Euler, Newton and Archimedes — if not better.
Riemann conjectured that the zeroes were all of the form $s= ^1/_2+it$ (except from so-called trivial zeroes). Proving Riemann right (or wrong) is today’s longstanding crucial pure math open problem, as it would explain the seeming observed randomness in the distribution of the primes.
As beautifully explained by Marcus du Sautoy in The Music of Primes, each zero of the zeta function is like an instrument that plays a note. Somehow, the intensity of a note is defined by the distance of the zero from Riemann’s critical line. All the notes played by all the zeroes then add up to produce the symphony of the distribution of primes. Now, we have noticed no pattern in this symphony. As far as we can tell, primes seem to be distributed randomly. In some sense, this means that we have “heard” none of the notes of the zeroes of the Riemann zeta function. And this, Riemann and others argue, is probably because zeroes are all playing their notes with the same intensity.
It’s almost not an analogy, actually! Just like functions that describe the distribution of primes can be decomposed into simpler notes, so can any musical sound. In fact, figuring out how to most naturally decompose sound into simpler, fundamental notes, is another of 19th Century major contributions to mathematics. It was Frenchman Joseph Fourier’s.
Fourier proved that any sound is made up of fundamental complex exponentials $e^{i \omega t}$. This is spectacular! First, it says that even real-life sounds are more naturally decomposed into functions with complex number outputs. But I’ve guessed you’ve got used to that by now!
You’ll get there! Second, Fourier’s decomposition has had uncountable applications, from MP3 and JPG compressions to the study of resonance and quantum mechanics, through cosmological study of matter distribution, and pure mathematics as well. Third, and finally, Fourier’s analysis is deeply mind-bending. Roughly, it asserts that any function is obtained by adding periodic ones… This sounds clearly false. But, in fact, it is (almost) true.
Topology
Gauss, Cauchy and Riemann’s studies of differentiable complex functions stressed more and more the importance of making a difference between global properties of functions and local properties.
A differentiable function is a function that we can easily approximate, typically by linear or parabolic approximations, as done below:
But, importantly, such linear or parabolic approximations are done at a location, and they are only valid around this location. This is what I mean when I say that derivatives only provide local information about a function. For instance, if I give you the favorite dish in Montpelier, New Hampshire, I’ll be giving you an information that’s only valid in Montpelier. It will be a good approximation for New Hampshire, but it cannot be generalized to the whole of America — and much less to the whole world.
Surprisingly, Riemann showed the relevancy of global properties of functions and shapes in the study of equations. For instance, Riemann showed that complex solutions to an equation like $y^2 = x^3-x$ could be regarded as a (now called Riemann) surface. Riemann went on showing that the global study of this surface — in particular, whether it has holes — could allow for deeper understandings of equations. But it took another giant of mathematics to systematize and revolutionize the local and global study of functions and shapes.
I’m talking about Frenchman Henri Poincaré. In a series of memoirs called Analysis Situs, Poincaré introduced a new kind of mathematics we now call (algebraic) topology. Therein, Poincaré defines what it means for two shapes to be homeomorphic. Namely, two shapes are homeomorphic if they can be continuously bent from one into the other. Importantly, such two shapes will have similar global properties, and can thus be considered globally identical. Poincaré then goes on constructing algebraic structures that allows him to identify globally-identical surfaces.
Granted… So let me tell you about something a bit simpler. One of Poincaré’s major insights was to generalize Riemann’s study of surfaces to higher-dimensional geometrical shapes, including the 3-dimensional space we call our universe. With this abstract approach, Poincaré could then mathematically ask the fundamental question: What is the shape of our universe?
At the end of the 5th supplement of his memoir on Analysis Situs, Poincaré was a bit embarrassed, as he tried to address the question of the shape of the universe. Namely, he wondered if his algebraic structures were powerful enough to distinguish the shapes of the universe. However, with a bold clairvoyance, he predicted that “this would take us too far”.
You bet! This question is known as the Poincaré conjecture. It took the combined efforts of many great minds of the 20th Century, like William Thurston and Richard Hamilton, and the masterpiece of the Russian mathematician Grigori Perelman to answer the Poincaré conjecture. At last, in the early 21st Century, we finally knew all possible geometries a 3-dimension space can have… Too bad Einstein showed that our actual space is actually a spacetime of dimension 4 — if not more!
It’s a question still beyond our reach, and it might take another century to answer it.
Definitely not! Topology has become one of the most important subfields of mathematics. At its heart, it is the study of the concept of proximity, applied to the description of any space you can think of. Since any concept of approximation necessarily builds upon that of proximity, analysis has found in topology the essence of what it studies. As a matter of fact, in the years following Poincaré’s publication of his theory of topology, more rigorous and more general topological concepts have led to the rich development of functional analysis, by other geniuses like David Hilbert, Maurice Fréchet and Stephan Banach. But there’s more!
What’s definitely more surprising is probably the amazing usefulness of topology in the study of whole numbers. Following works of Oscar Zariski, André Weil and others, the recently deceased giant Alexandre Grothendieck developed highly abstract topologies for structuring systems of equations. This allowed him to develop the same kinds of theories for equations in whole numbers as Poincaré’s for geometrical shapes. Such techniques led to profound insights, which are still being explored today.
It often takes decades for great pure mathematical ideas to spill over applied fields. But, trust me, topology definitely has had uncountable applications. The concepts of open sets, compactness, completeness and connectedness now appear in economics, biology, chemistry, cosmology, string theory, and many more fields!
Let’s Conclude
Instead of recapitulating the magnificent development of analysis we’ve covered in this article, from pi to infinite series, from calculus to differential equations, from complex analysis to topology, let me conclude by making a case for the importance of mathematics for all.
In school, you might have learned that a function was continuous if its graph can drawn without lifting the pencil. This intuitive approach to the concept of continuity seems like a right definition. But it’s not. It took centuries of mathematical developments by mankind’s greatest minds to get there, but mathematicians have succeeded in putting the concept of continuity on (relatively) solid grounds. From the outside, this may seem to be an unnecessary gigantic effort.
Well, for long, many mathematicians like Newton and Euler didn’t demand such amounts of rigour. Like most people, they content themselves with intuition and approximative concepts. But as mathematics progressed, many paradoxical results were found, and rigourists like Gauss, Cauchy or Weierstrass decided it was time to put analysis on firm grounds. They made sure (or at least, they tried to make sure) that mathematics would always make sense.
Definitely. Not only did they remove many paradoxes, but, more importantly, their tremendously laborious effort led to new insights, which have hugely expanded the scope of mathematics since! More than anything else, the history of analysis is a great display of the long-term gains of rigour. This rigour is what certifies that a constructed tower will stand for centuries, instead of requiring multiple patches to avoid its breakdown. It demands a lot of time and effort in the short run, but yields dramatic results in the long run.
My point is that learning mathematics is not (or should not be) mainly about learning its content. Don’t get me wrong, mathematics is beautiful. It is worth knowing about. But the main gain in learning mathematics is rather about learning the high level of rigour that only mathematics (and maybe computer science) demands. This rigour consists of making sure that we understand every logical step of a reasoning, so that we may spot gaps wherever there is one; it’s also about knowing whether we truly understand something. This extreme rigour is the supreme ability of human thoughts that only mathematics can teach.
This is why mathematics is hard. But it’s also why it is so rewarding.

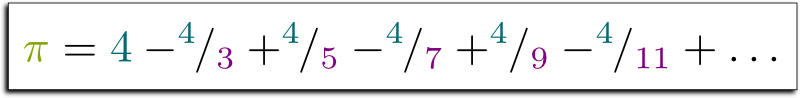


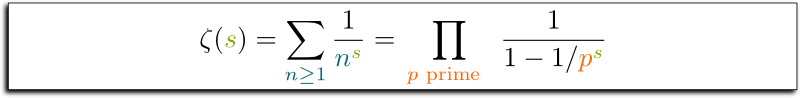

Leave a Reply