In this article, we’ll present and solve the classical utilities problem, using one of the most beautiful formulas of mathematics, due to Leonhard Euler. This will have us walking a few steps in the stunning world of algebraic topology! But first things first, let’s talk about the utilities problem!
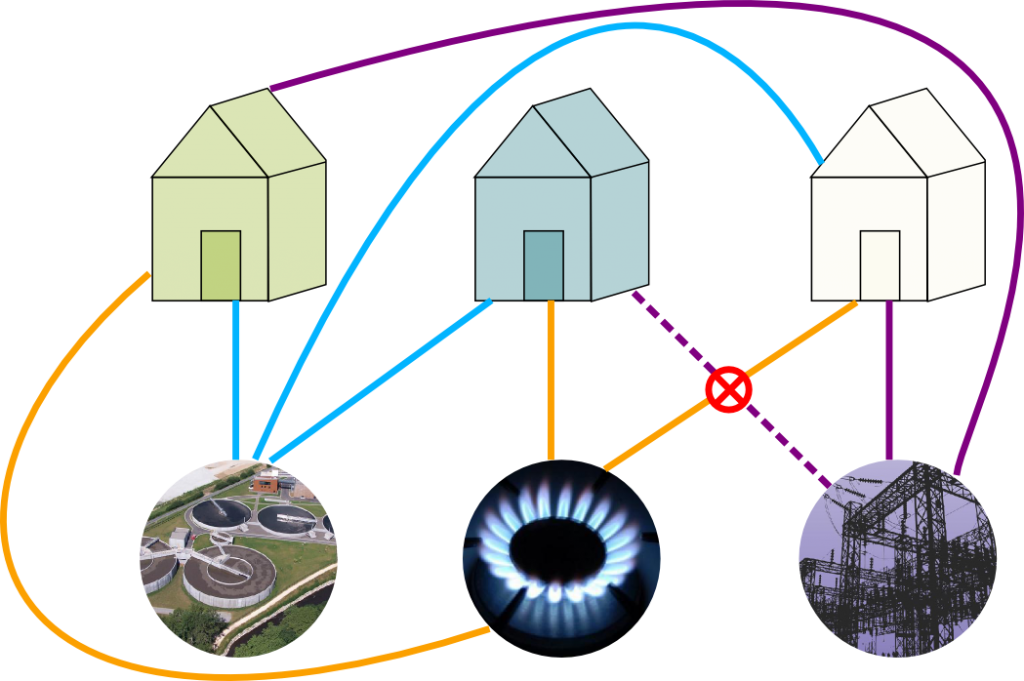
Three houses in a small village all need to be supplied with water, gas and electricity. Can you make all the connections between the houses and the supplies without having any two cable crossing?
Got it?
Let me try… Here’s what I got…
I know! I’m no better than you! But getting rid of this intersection is impossible. That’s what I was told when I was a kid, but it’s always frustrated me not to see why. Fortunately, I’ve recently discovered a proof. And it is beautiful!
Euler’s Formula for Planar Graphs
First, I need to talk to you a little bit about graph theory. Because that’s what we are dealing with here!
Graph theory is the study of connectivity between points called vertices. In our case, houses and supplies can all be modeled by such vertices. Now, our problem is to connect each house with all supplies with lines called edges. And avoiding intersections means that we want our graph to be planar. So, in graph theory terms, the problem consists in finding a planar graph connecting each of three vertices with all three other vertices.
You see right through me! But this will enable me to state the mighty Euler’s formula as it’s usually done!
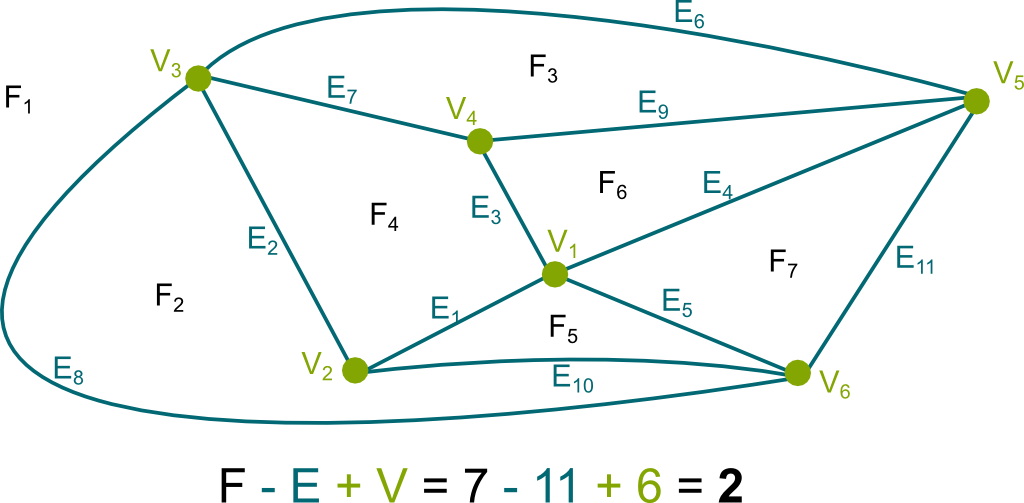
It says that, for any planar graph, $faces$-$edges$+$vertices$ always equals 2. Let’s see on the following figure.
Note that the outside of the graph has to be considered as 1 face for the formula to hold. This might seem arbitrary here, but it will make much more sense when we get to polyhedra…
If the graph is connected, yes!
I mean that all points should be joined through a sequence of edges. Learn more about connectedness with my article on topology!
Yes! And we can prove it! Actually, give it a try before I provide my proof!
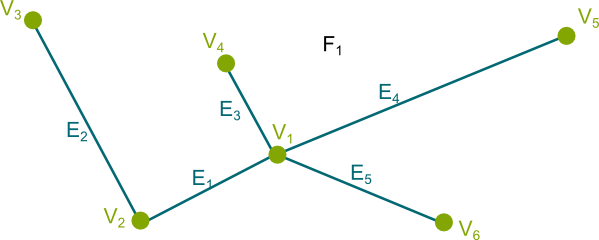
First, let’s remove all edges. Then, we add edges such that each added edge includes one more vertex to the vertices connected so far. So, for instance, we could consider edges $E_1$, $E_2$, $E_3$, $E_4$ and $E_5$. These 5 edges connect all 6 vertices.
We can easily check that, on this graph, Euler’s formula holds. Indeed, there’s only 1 face, and there are one more vertices than edges. I’m going a bit fast, but take your time to really follow through all I’m saying here. Thus, for the spanning tree, $faces$-$edges$+$vertices$=$2$.
We’ve already done most of the work! All we need now is to notice that, whenever we add an edge, we’re also creating a new face! Try it! Add $E_6$. Then $E_7$. And so on!
Thus, by adding the 6 missing edges, we’ve created 6 new faces. Eventually, the quantity $faces$-$edges$+$vertices$ gets added the 6 faces, but gets also subtracted the 6 edges. That’s why it remains unchanged: This proves Euler’s formula! To be perfectly rigorous in the general case, we’d need to involve a proof by induction, but I guess you get the idea!
Hehe…
The Solution to the Utilities Problem
First, using Euler’s formula, we can count the number of faces a solution to the utilities problem must have. Indeed, the solution must be a connected planar graph with 6 vertices. What’s more, there are 3 edges going out of each of the 3 houses. Thus, the solution must have 9 edges. Now, since $faces-edges+vertices=2$, we thus have…
Yes! Because of Euler’s formula, a solution to the utilities problem has necessarily 5 faces!
Now, we’ll show that this is incompatible with the structure of the graph of the utilities problem! And the key is to remark that all faces we create in the utilities problem have at least 4 sides!
Yes! In fact, you should spend some time finding out why on your own!
In other words, there can’t be any triangle!
Got it? Try a proof by contradiction: Assume that there is a triangle and show why that can’t be!
Then it has 3 vertices, right? Now, of what kind are the 3 vertices? Can they all be houses?
Exactly. Similarly, they can’t all be supplies. More interestingly, 2 of the 3 vertices can’t be of the same kind, since, as you said, there can’t be edges between two vertices of the same kind. So we have 3 vertices all of which have to be of a different kinds. But there are only 2 kinds of vertices. That’s where we get a contradiction.
No. Now, what’s interesting is the consequence on the number of edges! How many edges are required to make 5 faces, all having at least 4 sides?
Are you sure? Can’t edges be used several times?
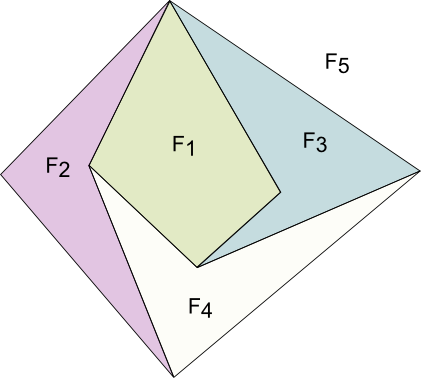
Yes! Thus, at least 10 edges are required to make 5 faces of 4 sides. On the right is an example of a graph with 5 faces of 4 sides and exactly 10 edges.
Bingo! We have a contradiction! To satisfy Euler’s formula, a solution must have at least 5 faces with at least 4 sides, which means that it has at least 10 edges. Yet, it also needs to have 9 edges, as required by the statement of the problem! Thus, such a solution does not exist!
To recapitulate, check this explanation by the great James Grime on SingingBanana:
Hehe… That’s because Euler’s formula was actually addressed to polyhedra rather than planar graphs. In fact, graph theory didn’t exist at that time! But the link between planar graphs and polyhedra with no holes is one of these extremely powerful connections in mathematics! This encounter was very fecund, as it gave birth to algebraic topology! Let’s explore it!
Euler’s Formula for Polyhedra
In short, Euler’s formula still holds for polyhedra with no holes. For instance, the cube has 6 faces, 12 edges and 8 vertices. Thus, $faces$-$edges$+$vertices$=$6-12+8=2$. It satisfies Euler’s formula!
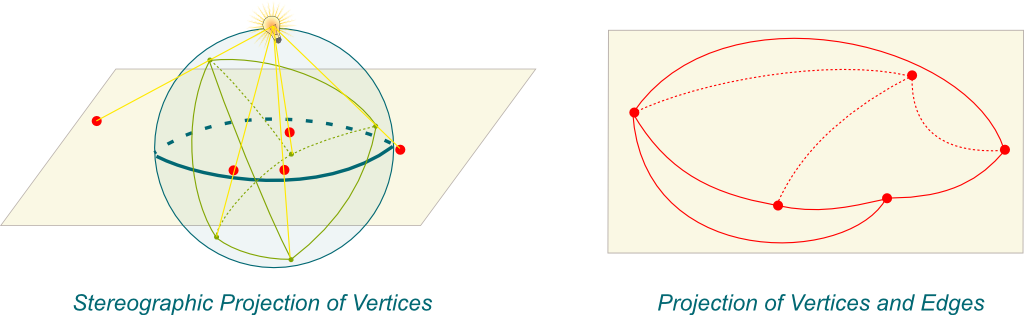
In two words, from the stereographic projection. This stereographic projection is beautifully explained in this extract from the series A Walk through Mathematics made by researchers and artists at ENS Lyon in France:
Let’ take a polyhedron with no hole. We can sort of blow it up to make it sphere-like. Then, let’s embed it inside a sphere and project it, by putting a lamp inside and observing the shadows drawn by the edges of the polyhedron on the sphere. This is what’s done in the following figure with quadrilateral-based pyramid:
Notice that if the polyhedron is convex (which means that it was indeed blown-up), then projected edges on the sphere should not intersect.
Now we use the stereographic projection! We can always turn a bit the sphere such that its North pole doesn’t match a vertex of the polyhedron nor an edge. Then, we’ll have a one-to-one match between the vertices and edges on the sphere with their stereographic projections on the plane. This is what’s done below:
The image obtained on the plane is then a graph. Now, if two edges of this graph intersects, then the intersection is the projection of an intersection of the two edges on the sphere. But, as we said, at least for convex polyhedra, there’s no such intersection for the polyhedron projected on the sphere. Thus, the graph projected on the plane is…
Bingo! And Euler’s formula holds for connected planar graphs. Now, there’s a one-to-one match between vertices, edges and faces of the initial polyhedron and the projected graph. Thus, Euler’s formula still holds for the original polyhedron with no hole! We have proved Euler’s formula!
Yes! You can check it out on your own. In particular, the front face of the pyramid that we see is mapped to…
I know!!! Euler’s formula has plenty of other beautiful proofs. Another brilliant one is given in this lecture by N.J. Wildberger. It’s worth checking it out!
Euler Characteristic
Some polyhedra cannot be blown-up into a sphere-like polyhedron! This is the case where they have holes. Below are two such examples. The first one is the famous Szilassi polyhedron. It also has the surprising property of having all of its 7 hexagonal faces all touching one another! Its discovery, made as late as 1977, was a shock in the mathematician community!
The surprises of these new objects have put forward the importance of the concept of holes in mathematics, and, in particular, in topology. A great example is the recent of proof of Poincaré conjecture by Perelman. And the Euler characteristic plays a key role in the understanding of these holes.
Haven’t you guessed? The Euler characteristic is the quantity we have been studying so far, that is, $\chi $=$ faces$-$edges$+$vertices$. I don’t know why, but it’s commonly denoted with this greek later $\chi$.
Yes!
Humm… Let me ask you a question. What’s a hole? Can you provide a clear definition of a what a hole is?
Haha! You can find it out with my article on Poincaré conjecture! Another cool definition of holes is based on the idea of cuts, as explained in this talk by Jason Ross.
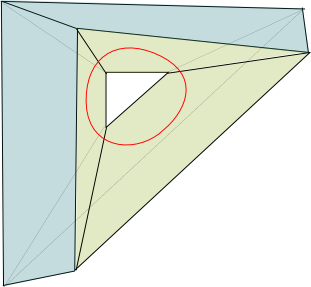
More formally, the number of holes, known as genus, is the maximum number of non-intersecting cuts along closed loops on the surface without disconnecting the object. This genus is usually defined for closed surfaces like the sphere or the torus, but it can also be defined for polyhedra. Both of the holed polyhedra I showed earlier have a genus equal to 1. The figure on the right illustrates a cut that can be done, along the drawn red loop.
We can say even more! If we denote $g$ the genus, then we have the following beautiful formula relating the genus to the Euler characteristic: $\chi = 2-2g$.
This formula is essential in algebraic topology for the classification of orientable closed surfaces.
The awesome question is rather: What’s a non-orientable surface? I’m dying to answer this question right now, but, for clarity, it’ll have to wait for a future article…
Now, closed surfaces are surfaces which are limited in space and have no boundary. Typically, this is the case of the sphere and the torus. Now, in fact, all closed surfaces which can be represented in our 3D world are orientable. So, don’t worry to much about orientability here.
Easy! First, it says that all orientable closed surfaces with genus 0 are continuous deformations of a sphere. For instance, a cube has genus 0, thus the cube can be deformed continuously into a sphere. We say that the cube is homeomorphic to the sphere. For a proper definition of homeomorphism, read my article on Poincaré conjecture.
Well, all orientable closed surfaces with genus 1 are homeomorphic to the torus. In particular, the two holed polyhedra above can be deformed continuously into tori. The following figure displays the deformation of the second holed polyhedron into a torus:
This construction is in fact what proves that the Euler characteristic of a torus is 0. Indeed, on the torus I drew above, we can retrieve the 9 faces, 18 edges and 9 vertices of the initial polyhedron!
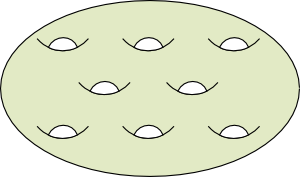
In the general case, an orientable close surface of genus $n$ will be homeomorphic to an $n$-holed torus. On the right is an example of an 8-holed torus.
The Utilities Problem on a Torus
Let’s get to what James Grime mentioned about the utility problems on a torus!
When we proved the non-existence of planar graphs, we actually used the fact that planar graphs have an Euler characteristic $\chi=2$ to deduce $faces=5$. But if we now consider graphs on a torus, then $\chi=0$, thus, $faces=3$. Thus, on a torus, we might no longer have any contradiction!
Indeed there is! Why don’t you spend some time searching for it?
To help you, keep in mind that a torus is like the map of PACMAN: It’s a rectangle such that, when you go out of the rectangle towards the right, you appear at the same height but on the left. Similarly, if you go up, then you reappear at the bottom with the same left-right position. I talk more about this in my article on Poincaré conjecture.
Did you find a solution?
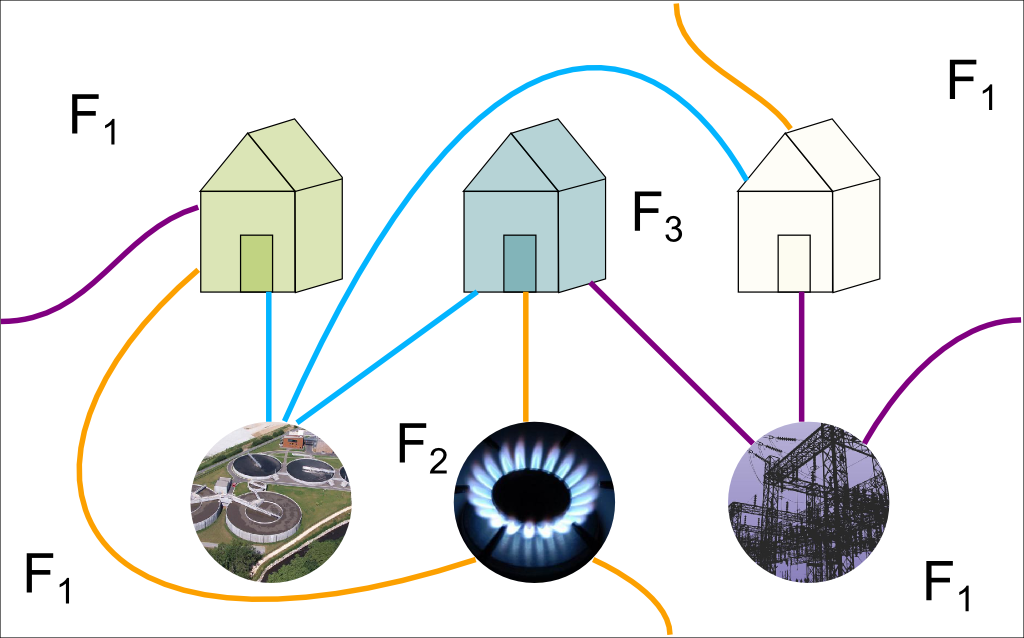
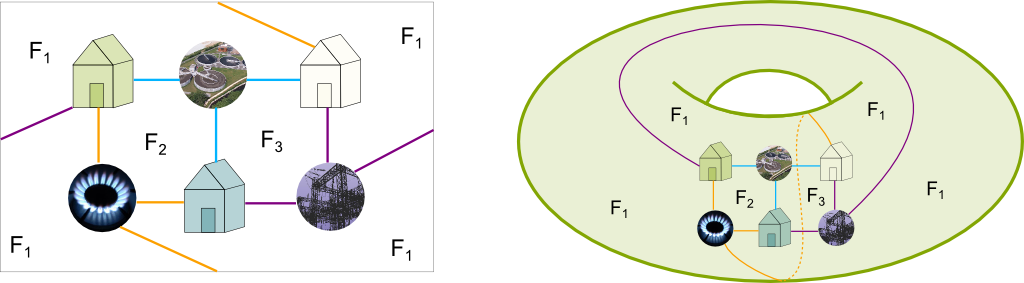
Great! Below is my solution to the utilities problem on a torus.
I’ve numbered the faces. The sides connect the four extreme areas, making up the face $F_1$. As you can see, as Euler’s formula predicted it, there are 3 faces.
Great reflex! Indeed, this graph has an Euler characteristic equal to 0. Now, let’s analyze the faces in more details. Faces $F_2$ and $F_3$ are quadrilaterals. Regarding $F_1$, all edges except the one bringing water to the blue house are its boundaries. It thus has 8 sides. This all makes up a total of 4+4+8=16 sides, which require 8 edges to be done. But we have 9 edges. Why?
Any idea?
Let’s move vertices and edges to have a clearer view at the graph! Note that there is only one edge connecting faces $F_2$ and $F_3$, so I’ve placed it in the middle. Then, I can reposition the houses and supplies so that $F_2$ and $F_3$ now form squares. This gives the figure on the left below. I can now even plot the graph on an actual torus, as done on the right!
Do you better see what happens?
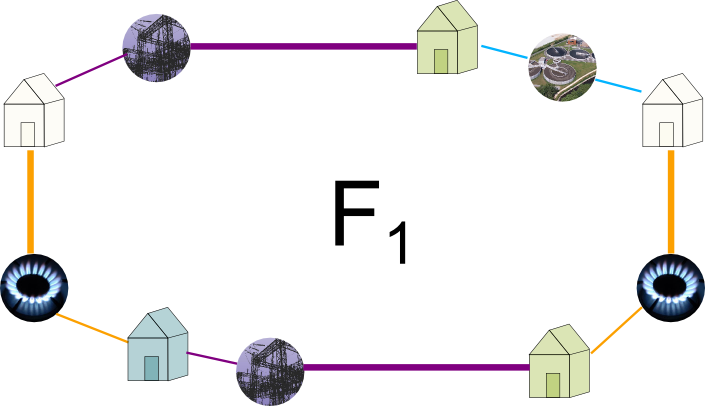
Yes! As a result, these two edges are sort of used to cut the torus to make it an actual face with no hole. And they thus appear twice as sides of the face $F_1$. This face thus actually has 10 sides! To better see it, let’s draw it!
As you can see the bold horizontal and vertical edges appear twice in $F_1$. If you’re familiar with algebraic topology, this figure should definitely ring a bell. If you’re not, wait for my future article on fundamental polygons. In the meantime, you should check Wikipedia’s article or follow Wildberger’s awesome course on algebraic topology!
Let’s Sum Up
We’ve been doing algebraic topology! How exciting is that?
Because closed surfaces are strongly related to homeomorphic polyhedra, the study of polyhedra has turned out to be essential to the understanding of topology and connectedness, which is studied by algebraic topology. And Euler’s formula thus plays a key role in this field. In fact, Euler characteristic can easily be generalized to higher dimensions. After all, it more or less adds the number of subelements of polyhedra of all dimensions, with a negative sign before odd dimensions. Better insights are given by homology… But that’s going to be for another article!
To finish, let me draw a strong connection between all we’ve discussed and the mythic 4 color theorem. I mention this theorem in this extract from my talk A Trek through 20th Century Mathematics.
Hehe. In fact, I’ve introduced in this article the object which immediately proves that you may need at least 7 colors to color a map on a torus! Can you find it?
No. Not my holed polyhedron…
Yes! Thus, all faces must have a different color than all others. This means that 7 colors are required to color Szilassi polyhedron! The not-4-color theorem on the torus sounds less troubling now, doesn’t it? Now, we still need to prove that 7 colors are sufficient, but I’ll let you work on that.
Finally, I’ve put a video of a talk by William Dunham on Euler in the references. Check it out! It’s absolutely amazing!




Leave a Reply