We saw in the post Cryptography and Number Theory, how centuries-old discoveries in theoretical mathematics turned out to have powerful applications for security for network-based fields such as online commerce and computerized voting. Recent discoveries in the branch of physics known as quantum mechanics also have applications in the field of internet security – they have the potential to break the forms of internet security based on mathematics, and also present new ways to safely send information. In this article we’ll see how a physics-based method can be used to secure online information.
Let’s Get Started…
In my post regarding “Cryptography and Number Theory”, we saw how online data is secured using public-key cryptography. When a message is sent between two parties, “Alice” and “Bob” – say, an ATM machine and your bank, or Amazon.com and your bank – it is sent using a public encryption key that can be viewed by anyone intercepting the message, and a private decryption key that is sent separately and is known only to the sender and the target. The security of the system relies on the mathematical difficulty involved in calculating the decryption key, which is necessary for decoding the encoded message: the encrypted message could be broadcast over the evening news, but without the decryption key, it would be nearly impossible for someone to break the encryption and read the message.
This is a major problem with forms of public-key cryptography such as the RSA algorithm: the eavesdropping problem. In order to ensure the security of a message sent using public-key cryptography, it is crucial that an eavesdropper not be allowed to view both the publicly known encrypted message and the private decryption method.
Cryptographers have discovered a way to use results in the branch of theoretical physics known as “quantum mechanics” to securely send a message over a public channel. What’s amazing about this is the fact that it does not rely on mathematical properties for its security – it relies on fundamental properties of the physical world.
To see how “quantum cryptography” works, let’s first explore a bit of the counter-intuitive properties that govern the physical world’s behavior at the subatomic level.
Some Basic Findings of Quantum Mechanics
The word “quantum” comes from the Latin for “how much”, and refers to counter-intuitive properties of subatomic particles discovered beginning in the late 1800’s and early 1900’s CE. The field arose out of the study of electromagnetism, where physicists found that electromagnetic waves such as light beams can be described both as waves and as streams of discrete particles, or “quanta”.
It turns out that the universe behaves in apparently contradictory ways when studied at the sub-atomic level. In fact, the physicist Richard Feynman, stated that it is impossible to understand quantum mechanics, due to the paradoxical ways the universe behaves at the subatomic level. Feynman was known for his research and teaching skills: he won the 1965 Nobel Prize in Physics, and was also a devoted teacher whose series of lectures on physics have drawn much acclaim.
Thanks to Bill Gates, these lectures are now available for free on the internet.
While it’s difficult to understand quantum mechanics in the “commonsense” way we can understand classical, everyday physics, given the paradoxical results found at the subatomic level, it is still worthwhile to study, however, both for better understanding of the universe, as well as promising applications the field offers for technology.
Let’s look at a few examples of basic principles of quantum mechanics to get a taste for the paradoxical ways in which the universe behaves at the quantum level. We’ll then see how to use these findings to devise a secure system of quantum cryptography.
Photon polarization
One of the fundamental concepts of quantum mechanics suggests that particles like photons have properties of both waves (like radio waves) and particles (like concrete objects). As a photon particle travels, its electric and magnetic fields vary, but are always perpendicular to each other and perpendicular to the direction of the photon’s travel. The direction in which the electromagnetic field varies is known as its “polarization”. It can vary in different ways, including linearly (up and down, like waves in an ocean) and circularly (twisting in a spiral shape around the direction of motion).
Check out this video demonstrating the distinction between these types of polarization.
Photon polarization comes into play in quantum cryptography due to discoveries regarding pairs of subatomic particles that originate from a common point in space-time. This is known as “quantum entanglement”.
Quantum Entanglement: “Spooky Action at a Distance”
Experiments and theoretical developments have shown that it is possible for two subatomic particles to become “entangled” in such a way that, when a given property of one of the particles is observed, the opposite state will then be observed in the second particle, regardless of the distance between the two. For example, when two entangled photons are sent along a channel, and one is observed as having a certain linear polarization (in a specific direction), then the other will be seen to have the opposite polarization. It is not possible to share information in this manner, since the state the electron is observed in cannot be known in advance.
Above is a NASA picture from an experiment involving laser beams composed of entangled photons.
Not quite, though it is very useful for research and, as we shall see, technology development. Quantum entanglement is a natural phenomenon that occurs when two particles originate at the same point in space and time, for example. The simple act of measurement on one of the particles leads to a measurable difference in the other particle (not matter how far away). Einstein famously described this as “spooky action at a distance”, and was not satisfied with QM due to its paradoxical nature. Around 30 years later, and after Einstein’s death in 1955, the physicist John Bell was able to build a framework in which quantum entanglement makes sense, by using the notion of “non-locality”. Let’s see how he did this.
Bell’s Theorem
The set of theoretical and experimental results known collectively as Bell’s Theorem is considered by some among the most profound discoveries of the past century. It suggests that the way the universe behaves at the quantum level is fundamentally different from how it appears to behave at the larger, everyday level studied in classical physics. More specifically, Bell’s Theorem shows that QM is inherently a non-local theory of physics: it implies that, under certain circumstances, taking a measurement on one particle can instantly influence the behavior of another particle, however far away.
Well as Feynman suggested, no one fully understands why this is so, but Bell’s theorem has been confirmed in laboratory experiments such as the famed ones run by researcher Alain Aspect (which utilized polarized photons), so it’s clear that at subatomic levels, the act of making an observation of a system can actually influence the state of that system. The early quantum physicist Heisenberg suggested that observing or measuring a particle caused photons to impart energy to the particle, leading to influence on its behavior, but a recent study showed that the act of measuring introduces less uncertainty than quantum mechanics models such as Heisenberg’s Uncertainty Principle require. So physicists don’t have a full explanation for why the universe behaves in such paradoxical ways at the quantum level, but experiments have established that it does in fact operate in the way quantum mechanics describes.
Check out Spooky Action at a Distance for an in-depth discussion of how Bell’s Theorem was established.
Amazingly, we can take advantage of these properties of quantum physics – polarized photons, quantum entanglement, Bell’s Theorem, and the Heisenberg Uncertainty Principle – to establish a system of cryptography that is fundamentally more advanced than current mathematics-based cryptography systems. Let’s see how to do this.
Quantum Key Distribution
We will devise a “quantum channel” consisting of entangled photons that are used to share a key – an encryption and decryption scheme – in such a way that it will become apparent if an eavesdropper is spying on the communication. If an eavesdropper spies on the “quantum channel”, their measurements of the photons will influence the photons’ polarization and thus be detectable. Thus, quantum mechanics can be used to guarantee that the key is sent in secrecy. Once the key is established the encrypted message can be sent over public channels – even announced on the evening news – with guaranteed security. All communication between the sender and receiver is on public channels, but the key is distributed via the private, quantum channel, which enables the detection of eavesdropping.
Eckert’s Protocol
Artur Eckert, in a 1991 paper, used Bell’s Theorem and quantum entanglement to develop a quantum channel over which a key can be securely shared. In Eckert’s scheme, before attempting to share a message, the sender and receiver use a quantum mechanics-based scheme to develop a key. The sender and receiver – let’s call them Alice and Bob – are sent a pair of entangled photons. They each randomly choose a set of bases through which to measure these particles, and then measure the photons’ polarizations. They announce in public which bases they used to obtain their measurements, and then split their measurements into two groups: (1) those in which they used the same basis of measurement, and (2) those in which they used different bases.
In order to determine whether the quantum key transmission has been intercepted, they examine the results of the measurements they made using differing bases. If the entangled photons have been measured prior to their receipt by Alice and Bob, the interception will be detectable due to the properties of quantum mechanics we’ve seen. So Alice and Bob publicly share the measurements they made using differing bases, and use probabilistic calculations given by Bell’s Theorem to determine whether or not the particles have been observed. The mathematics behind this is a little too in-depth to present in this article, which is primarily about the underlying physics, but if you’re interested, check out Eckert’s 1991 paper).
If Alice and Bob determine that the entangled particles have not been observed by an outside party, then they can be sure that the quantum channel is secure. They can then use the observations they made using the same basis – which, according to the principle of quantum entanglement – to calculate a key by which to encrypt and decrypt their message. The way they do this is to label certain polarizations (such as a linear polarization in the positive x-axis) as “0”, and others (such as a linear polarization at a 45 degree angle from the x-axis) as “1”. They can then turn the measured polarizations into a sequence of 0’s and 1’s. Alice and Bob will each arrive at a sequence of 0’s and 1’s, but since the polarizations they measure using the same basis will be opposite (due to principles of quantum entanglement), their strings of 0’s and 1’s will be exactly the inverse of each other. If one of them obtains the string 011001…, the other will obtain 100110…so one of them simply inverts their string.
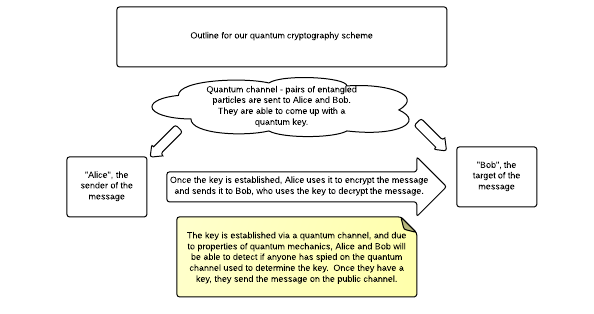
To reiterate this, here’s a diagram of Eckert’s quantum key distribution scheme.
In the scheme, pairs of entangled photons are sent to Alice and Bob, who then measure their polarizations using randomly chosen bases. They then share in public the bases they have used, and split them into two groups.
- Measurements for which they used the same basis.
- Measurements for which they used different bases.
The measurements for which they used different bases are used to determine whether someone has eavesdropped on the quantum key transmission. Recall that if someone makes an observation or measurement of the polarization of the photon, this will effect the measurements Alice and Bob make. They can use Bell’s Theorem to calculate whether someone has eavesdropped by performing statistical tests on the measurements they have made using different bases.
If they determine the quantum key has been sent securely, then they use the measurements for which they used the same basis to form a secret key. According to properties of quantum entanglement, when Alice and Bob use the same basis to measure the polarization of two entangled photons, their measured polarizations will be exactly opposite each other.
Once they have this key, Alice can encrypt her message and send it to Bob over a public channel, secure in the knowledge that no one has observed the way in which they developed their scheme.
To sum it all up…
We have taken an overview of the basic results of quantum mechanics, the branch of physics that studies the properties of the universe at the subatomic level, and seen how to use this to develop a cryptographic scheme that is secure against eavesdropping. QM has shown that the act of taking a measurement on a particle can effect the behavior of other, “entangled” particles, and we can use this property to find whether an eavesdropper has observed the transmission of a key used for encrypting and decrypting a message.
The security of quantum cryptography is therefore based in properties of physics known in quantum mechanics, rather than any mathematical method of encryption and decryption. As long as quantum mechanics’ description of reality is complete, cryptography will be completely secure.
The main problem with quantum cryptography is the difficulty of actually implementing it. Sending entangled photons over large distances is a significant technological problem to overcome. At the moment, conventional, public-key cryptography schemes such as RSA, whose security relies on mathematics rather than physics, are the most widely used, but in the future, many cryptologists think, these will be easily broken by more advanced computers, and physics-based schemes such as the quantum cryptography schemes are seen as their natural replacement.
The first real-world application of quantum cryptography was in the Swiss election of October 2007. More recently, scientists have discovered a way to use existing broadband cable to carry out the quantum key distribution schemes, overcoming one significant technological challenge for QKD. Companies such as MagiqTech offer concrete quantum key distribution system for researchers who are working to make this kind of encryption practical and feasible in the modern world.



Leave a Reply