Of the seven millenium prize problems, Poincaré conjecture is the only solved one. Conjectured by French mathematician Henri Poincaré (who, by the way, went through the same University as I did!!!), it was solved by Russian mathematician Gregori Perelman in 2003. This article explains what the conjecture says.
Homeomorphism
Poincaré conjecture is a problem of topology, which is a subfield of mathematics which studies properties of connectedness of spaces. In particular, topology aims at continuously deforming spaces into simpler better-known spaces. For instance, in the animation from Wikipedia on the right, a mug is continuously deformed into a doughnut. This continuous deformation is called a homeomorphism.
Not exactly. In order to have the topological properties preserved, topologists also want homeomorphisms to be invertible, and that the inversion is continuous too. This means that, not only do we need to be able to deform continuously the mug into a doughnut, but we also need to be able to invert continuously the doughnut back into a mug. In more precise terms, a homeomorphism is a continuous one-to-one mapping between two topological sets whose inverse is continuous too.
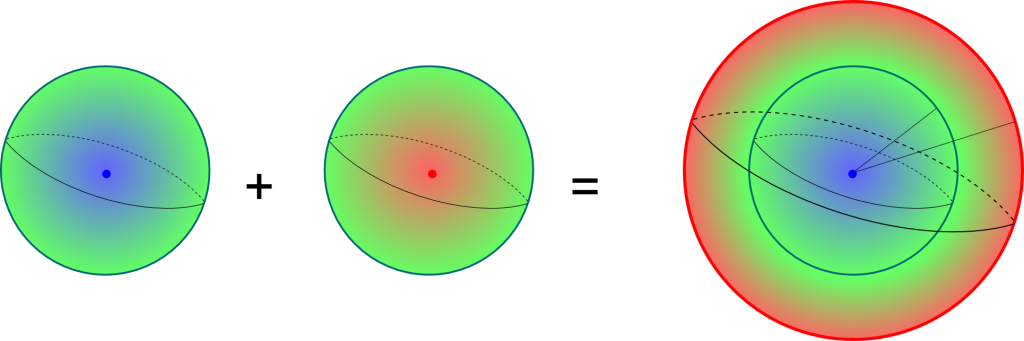
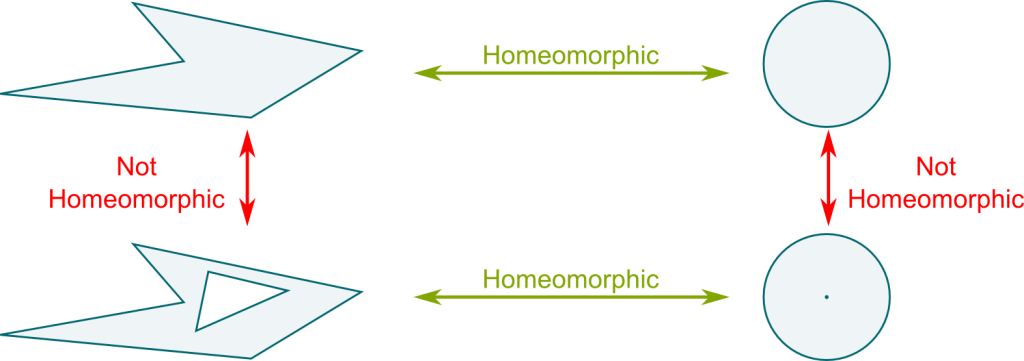
Visually, it’s very simple. Basically, homeomorphisms involve stretchings and contractions, but forbid cuts and pastes. This means, for instance, that disconnected spaces cannot be connected by a homeomorphisms. Below are several examples of homeomorphic spaces.
Notice that the two spaces above are not homeomorphic to the two spaces below. This can proved by remarking that the two spaces above have one connected boundary. On the other hand, the two spaces below have a disconnected boundary. Since borders cannot be cut nor pasted, there is no way of deforming these of the above spaces into these of the below spaces.
This definitely enables to tell non-homeomorphic spaces apart. But two spaces with equal number of connected components, and whose boundaries are also made of the same number of connected components, are not necessarily homeomorphic. To better understand this, Poincaré focused on connected spaces with no boundary. Also he only considered bounded spaces, as opposed to spaces which go to infinity like a plane. Technically, these spaces are defined as compact spaces with a dimension n such that, if you zoom enough around any of point, the space looks like a n-dimensional vector space. They are called closed n-manifolds. A 1-manifold is a curve, while a 2-manifold is a surface.
Sure. In fact, the examples I’m going to give will be essential to discuss Poincaré conjecture. First is the simplest closed 2-manifold, namely, the sphere. If you zoom in on a sphere, the surface of the sphere looks like a plane, which is the 2-dimensional vector space. A sphere is thus a 2-manifold. Plus, it is compact since it is bounded.
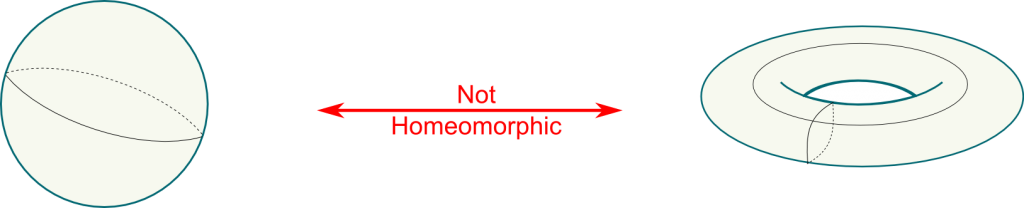
The other important closed 2-manifold is the torus, which is basically the surface of the doughnut I mentioned earlier. What’s important to note is that, even though the torus and the sphere are both closed 2-manifolds, they are not homeomorphic!
This is an awesome question to leads me to Poincaré’s key insight.
Homotopy
Poincaré’s key insight was to consider loops made on a figure. This study of loops is called homotopy. Listen to myself explaining this idea in this extract from a Trek through 20th Century Mathematics.
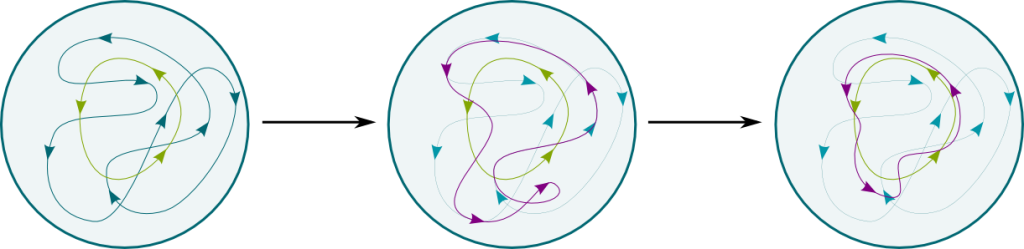
Yes! Exactly. But one thing to notice is that some loops are essentially equivalent. This is the case whenever one can be deformed continuously into the other. We say that such loops are homotopic. For instance, in the following figure, the purple loop displays the continuous deformation of the blue loop into the green loop. Thus, the blue and green loops are homotopic.
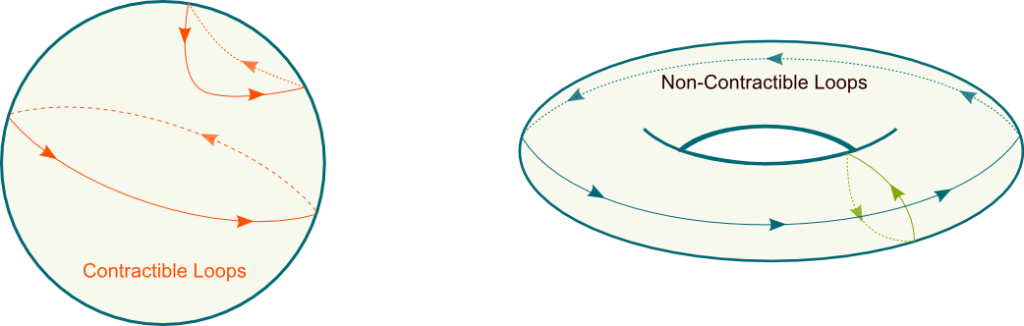
In fact, you can even notice that these loops can be deformed into a point. They are thus homotopic to points. We say that these loops are contractible. They sort of represent the zero of homotopy.
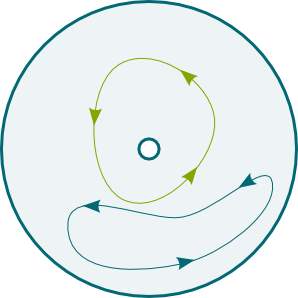
Well, it depends on the structure of the space we study. In the holed disk on the right, the blue and green loops cannot be deformed into one another. They are not homotopic. In particular, the blue loop is contractible, while the green loop isn’t.
Homeomorphism preserves homotopy.
Sure! Consider a disk and a polygon, and a homeomorphism between them. Let a green and a blue loop of the disk. Each point of each loop is thus uniquely mapped with a point of the polygon. Overall, each loop of the disk is uniquely mapped with a loop of the polygon. Thus, the green and blue loops of the disk are mapped with a green and a blue loop of the polygon.
When I say that homeomorphism preserves homotopy, I mean that the green and blue loops of the disk are homotopic if and only if their images in the polygon are homotopic.
Let’s prove it! Assume that, in the disk, the green and blue loops are homotopic. Then there are purple loops which are intermediate loops from the blue to the green loop. Each purple loop of the disk is mapped with a purple loop of the polygon. The obtained purple loops of the polygon now form a transition from the blue to the green loop in the polygon. Thus, the image of homotopic loops by the homeomorphism are homotopic too. A similar reasoning shows that homotopic loops of the polygon are associated with homotopic loops of the disk by the inverse homeomorphism.
We only need to prove that there are loops on a torus which do not correspond to any loop on a sphere. The key argument is that all loops on a sphere are contractible, while the torus has the two non-contractible blue and green loops drawn below. If there were a homeomorphism, then the image of the blue and green loops in the sphere would be non-contractible, which contradicts the fact that loops on a sphere are all contractible. Thus, the sphere and the torus are not homeomorphic.
Surfaces in 3 dimensions are hard to visualize indeed. Fortunately, there is a much simpler way to describe two-dimensional surfaces using planar representations and… glue.
Planar Representations
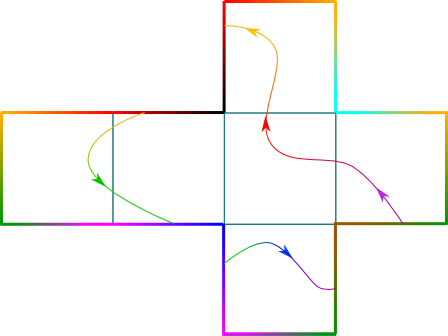
Yes! You have probably learned at school that you could make a cube using a net like the one on the right, and by then gluing the sides in the right way. This right way is represented by colors on the edge. Same colors must be glued together. We can describe loops on the cube by describing the loops on the net. Isn’t this planar representation much simpler to visualize?
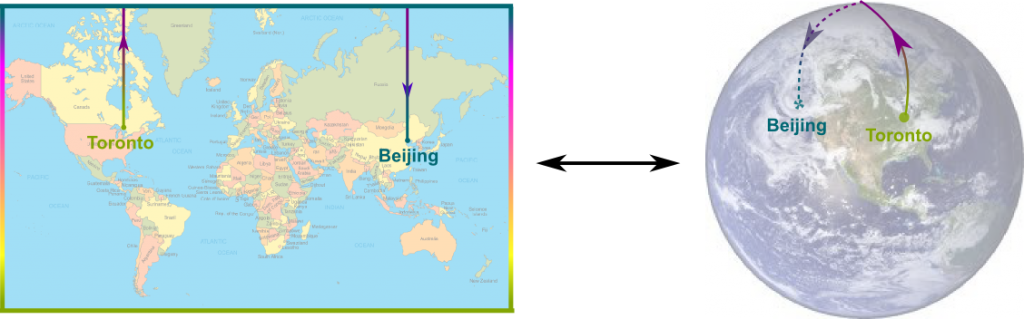
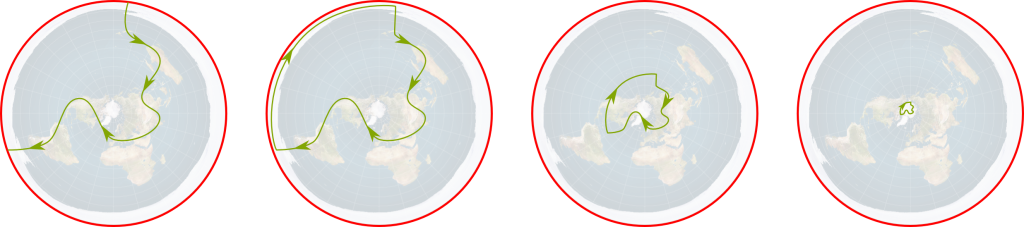
Yes! For instance, the Earth is usually represented by a 2-dimensional map. However, the gluing of the map is a bit more complicated, as the whole top of the map should be glued together as the North Pole. Now, when I took a flight from Toronto to Beijing, the plane went through the North pole. This can be nicely represented on the map:
No. Although common to us all, the map drawn above is a bit too complicated in terms of gluing, as there are four sides with different properties. Rather, let’s work on the most simple representation of the sphere, which is a disk centered on the North pole. The edge of the disk corresponds to the South pole, and should thus be all glued together.
By the way, this representation is great to visualize the fact that the shortest path from Toronto to Beijing does go through the North pole. Find out more about map making with Scott’s article on non-Euclidean geometry.
All the points of the edge of the disk are one single point. Thus, a path disappearing at one end and reappearing at another end can be deformed into a path going along the edge, as done below.
The deformed loop can then be contracted to a point.
Consider any loop on the sphere. We can deform it such that it never crosses the South pole. This deformed loop doesn’t cross the edge of the disk. It can then thus be contracted to a point by a homothety centered on the North pole. You can learn about homothety with my article on symmetries.
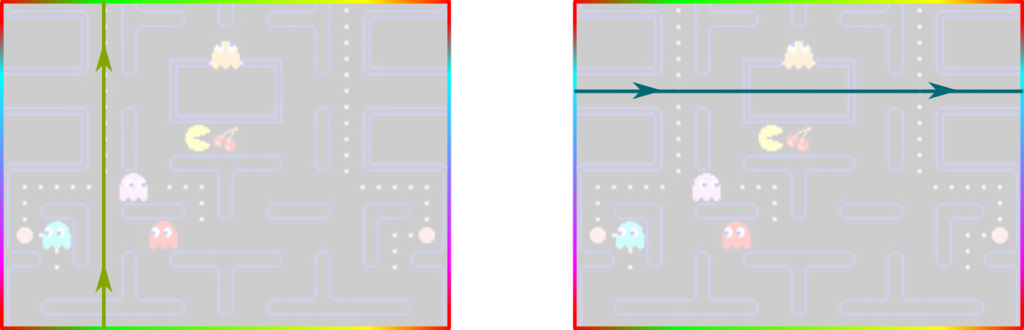
Hehe… The torus is actually a square with opposite sides glued together, exactly like in one of History’s greatest video game, PAC-MAN. If this is missing of your culture, I feel sorry for you! But I’ll explain it nevertheless. PAC-MAN is played on a screen. Whenever you go out of the screen on the right, you reappear on the left. Similarly, when you go out out of the screen on the top, you reappear on the bottom.
As we first glue the top with the bottom, we obtain a cylinder. We now needs to glue the end sections of the cylinder, which can be done by curving the cylinder. We obtain the following figure:
Check out this animation by Youtube channel Geometric Animations of the transformation I described above:
Non-contractible loops in the square representation are those which cross the edges. The two non-contractible loops we represented on the torus earlier are now represented as follows:
Let’s consider the green loop. The reasoning for the blue one will be similar.
That’s because it crosses the top edge. In fact, for any continuous deformation of the green loop, we can track the intersection of the deformed loop with the top edge, which proves that it cannot disappear. Similarly, we can draw a horizontal line in the middle of the square, and any deformation of the loop would also have to cross this horizontal line. Thus, any deformation of the green loop must intersect both the top edge and the middle horizontal line. It can therefore not be contracted to a point. This proves that the green loop is not contractible.
Exactly! More generally, we now know that any space with non-contractible loop is not homeomorphic to a sphere.
No. Poincaré conjecture concerns the reciprocal phrase. Namely, it asks whether closed surfaces with no non-contractible loop are homeomorphic to a sphere…
Poincaré Conjecture
Poincaré gave a name to these surfaces and spaces with no non-contractible loop. He called them simply connected. Poincaré managed to prove the result for two-dimensional manifolds, also known as surfaces. His theorem is one of these amazingly simple ones, as it can be written with 10 words:
Theorem: Any closed simply-connected surface is homeomorphic to a sphere.
Unfortunately, the only proofs I know, which involve the classification of 2-dimensional closed surfaces with technics of cutting and gluing, would be too long to explain here. These are nice proofs with no really technical difficulty. You can check it out in this great lecture by Norman Wildberger.
No. Poincaré conjecture concerns higher dimension manifolds. In dimension n greater or equal to 2, Poincaré conjecture is stated as follows:
Theorem: Any closed simply connected n-manifold is homeomorphic to a n-sphere.
You should now be able to understand every single word here except one…
That’s the one! A n-sphere is defined as the set of points at distance 1 to the origin in a (n+1)-dimensional normed vector space.
Hummm… Tough one. I give up for high dimensions, but I can provide a representation for dimension 3. A 3-sphere is the interior of the 2-sphere whose boundary is glued as a single point, in a similar way that we have described the 2-sphere with the interior of a 1-sphere. The interior of a n-sphere is known as a (n+1)-ball. So, in other words, a 3-sphere is a 3-ball whose boundary is glued into a single point.
It does! One construction consists in noting that a point on the 3-sphere lying in the 4 dimensional space is nearly known by 3 of its coordinates. In fact, if the 3 coordinates form a vector which belongs to a 3-ball, there is exactly 2 possible values for the last coordinate, which sort of correspond to the North and the South hemi-3-sphere. And if the 3 coordinates belong to the 2-sphere, then the 4th coordinate is uniquely defined. This corresponds to a sort of 2-dimension equator which belongs to both hemi-3-sphere. As a result, the 3-sphere can be thought as the union of two 3-balls which are to be glued along their boundaries.
Check this nice animation by Patrick Massot where the two hemi-3-sphere of the 3-sphere are displayed separately.
And we can glue these boundaries by inverting one of the 3-balls as follows:
Note that the center of the second 3-ball is inverted into the boundary of the final 3-ball. The final 3-ball can then be resized such that his radius equals 1. We eventually obtain a 3-ball whose boundary should be all glued together as one single point.
Yes! In fact, this construction is more general and works for any n-sphere. Any n-sphere is thus a n-ball whose boundary is a single point. By deforming loops such that they never reach this point, we can then prove that any loop is homotopic to a loop which belongs to the n-ball, and can thus be contracted using a mere homothety. This proves that any n-sphere is simply connected.
Yes, but this is a much more difficult problem. In fact, in 1904, Poincaré himself wrote: this question would take us too far (cette question nous entraînerait trop loin). He was definitely right! It took mathematicians a century to finally solve it entirely. Progresses have been made steadily, as the theorem was first proven in the 1960s for dimensions 7 and higher. Amusingly, the smaller the dimension, the harder the problem. In 1982, dimension 4 was solved, and there was only the problem in dimension 3 left.
Yes. And this came as a surprise, as he methods were definitely not conventional in topology.
.jpg/300px-Perelman,_Grigori_(1966).jpg)
Topologists mainly use technics of cutting and pasting like those I’ve presented in this article. But Perelman’s method rather consisted in using the dynamics of heated objects to prove Poincaré conjecture.
Yes. The idea is that, as objects get heated, they become rounder and rounder. More curved portions get straightened quicker. Eventually, they become spheres. By using this idea to deform the geometry of spaces, Perelman proved that all 3-manifolds could be deformed into one of the fundamental classes of closed 3-manifolds.
So let’s see another of Patrick Massot’s animations:
In particular, if the initial 3-manifold is simply connected, it gets deformed into the 3-sphere. Which proves the Poincaré conjecture.
Let’s Conclude
Poincaré conjecture has been a cornerstone for the classification of closed manifolds. While closed surfaces have been classified mainly by Bernhard Riemann, the classification of closed 3-manifolds had a deep connection with Poincaré conjecture. In 1982, William Thurston, probably the greatest topologist of the 20th century, conjectured that the geometry of any closed 3-manifold could be classified as one of 8 possible geometries. Perelman’s proof, along with Poincaré conjecture, answered Thurston’s conjecture positively.
There is a lot more to be said in topology of closed manifolds. For one thing, it has strong connections with graph theory and polyhedra, as you can read it in my article on the utilities problem. Also, I plan on writing an article soon on the amazing non-orientable surfaces, which involve the Möbius band, the projective plane or the Klein bottle. Stay tuned!