In 2012, mathematics has given birth to a new baby. And she is beautiful! Her parents, Vincent Borrelli, Saïd Jabrane, Francis Lazarus, Boris Thibert and Damien Rohmer, who formed the Hévéa project, have named her the first $\mathcal C^1$ isometric embedding of the flat square torus. Sexy, right? Have a look at the first video ever taken of her:
OK, her name is a bit long so I’ll just call her the Hévéa Torus.
Amazingly, she was first imagined a century and a half ago, by her ancestors Carl Friedrich Gauss and Bernhard Riemann, in 1854. But it took a century for her great grandfather John Nash to actually prove that she could one day be conceived, although he didn’t specify how. Another 20 years later, her grandfather Benoît Mandelbrot laid the foundations of a new kind of geometry which hinted at an actual possible conception. But, weirdly enough, it took the advent of computers to finally procreate her, after 5 long years of top-level mathematics research! And yet, it all started with a very simple problem…
Bending the Flat Square Torus
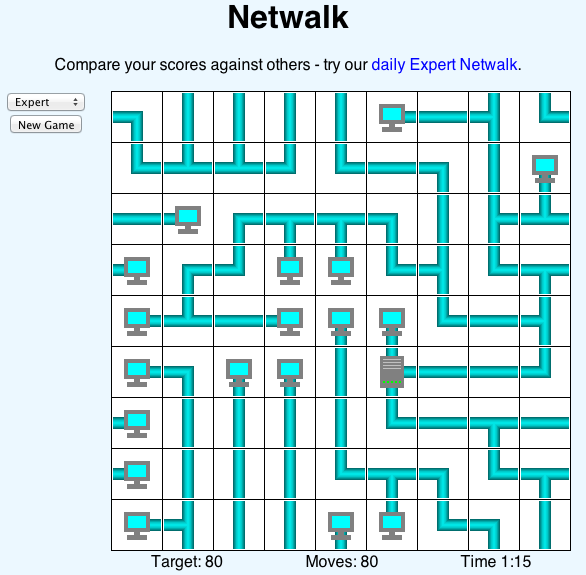
These days, I’m spending way too much time playing the game on the right called Netwalk where a network needs to be built. The game is played within a square. One tricky aspect is that whenever you get out of the square on the right, you reappear on the left. Like in PACMAN, or in these awesome games.
Amazingly, the network universe and the Hévéa Torus are geometrically identical!
You’re right. From our perspective, these are very different. But, from the perspective of some being stuck within these 2D worlds, there is absolutely no difference! The Netwalk world and the Hévéa Torus are intrinsically mathematically (nearly) identical.
You’re not the only one! It took two of the greatest giants of mathematics to figure out what it meant to live within a torus. The first one is Carl Friedrich Gauss, also known as the Prince of mathematics, who famously proved the Theorema Egregium, which you can learn more about by reading Scott’s article on non-Euclidean geometry. But, more importantly, it was Bernhard Riemann, Gauss’ disciple, who unlocked the wider geometry of so-called manifolds by providing a powerful new picture of what geometry could be.
In short, a Riemannian manifold is a space, such that each local neighborhood of a point of that space looks flat. The torus of the video is an example of a 2-dimension manifold, also known as surface. Around each point, if you zoom sufficiently, then your surface will look like a 2-dimensional sheet of paper. And, on this sheet of paper, lengths and angles are the same as on actual sheets of paper!
Now, involving lengths and angles makes things complicated… so let’s start with a simpler kind of manifold: The topological torus.
Topology is the art of forgetting the geometrical concepts of angles and lengths. This means that topology allows stretching sheets of paper without effectively changing it.
Sure! Topologically, it is straightforward to transform the Netwalk square into a torus. We merely have to glue together opposite sides. This is what’s done below:
This procedure of gluing is also described by this beautiful video by Geometric Animations:
Nash’s Isometric Embedding
The trouble is that, as you can feel it while watching this video, it seems impossible to glue opposite sides without stretching the square we started with.
It is! This no-stretching requirement corresponds to an isometry. To get a sense of the constraint that isometry represents, check this awesome video by Colm Kelleher on TedEd, which explains how isometry can prevent the tip of your pizza from falling down:
As the video explains it, it’s impossible to bend a sheet of paper into a sphere, or into a potato chip. This is because of the curvatures of these shapes. And the classical smooth donut-like torus is highly curved too, so it’s impossible to bend the flat Netwalk world into that classical torus. An isometric bending of the Netwalk world requires to transform it into an non-curved torus!
You’re not the only one! 60 years ago, most mathematicians even thought it was impossible! But no one could prove it. In fact, when deeply annoyed by his young, brilliant and pretentious colleague, MIT mathematician Ambrose Warren rashly retorted to him: “If you’re so good, why don’t you solve the [100-year-old isometric] embedding problem for manifolds“, which the bending of the Netwalk world with no stretching is an example of. Warren was hoping it would thereby keep his colleague busy for the rest of his life. But shortly later, that colleague was claiming he had solved it!
He was the founder of game theory, future winner of a Nobel prize in economics and future hero of the movie A Beautiful Mind… John Forbes Nash.
Not really… As I said, the young Nash was a pretentious douchebag. After all, he had just completed a revolutionary 28-page PhD thesis, and he was visibly smarter than most of his colleagues. So, he figured out that only a prestigious problem was worthy of his time. One that would mark History. So, to test whether the isometric embedding problem was of that kind, Nash looked at the reactions of his colleagues as he told them he had cracked it. And surely enough, it seemed that solving the isometric embedding would mark History. So, Nash decided to give it a try.
Amazingly, he did! Nash might have been showy, he’s also definitely a world-class mathematician.
The answer is yes. It can. Sort of… I’ve explained it all in this Science4All video:
So, as it turned out, Nash proved that we could, provided the bent torus had an infinite number of points on which acceleration could not be defined!
Here’s an illustration of what that means. Imagine a skater rolling down a slope:
In the first case, there is a huge discontinuity in the slope at the green point. In some sense, the slope cannot be defined at that point. In the third case, the slope is so smooth that the skater doesn’t feel anything special at this point. Finally, and most interestingly, in the second case, at the green point, the skater will suddenly feel a force acting on him which was not here before. Nash proved that this second case must happen at an infinite amount of times on the bent torus.
Nash’s claim means that Newton’s laws of mechanics would have no sense in the bent torus on an infinite amount of points, kind of like general relativity no longer makes sense at singularities better known as black holes!
I know! In fact, it was so sick that Nash couldn’t provide an example of a bent square torus! His proof was not constructive. He merely showed that there must be a way to bend a square into a torus, but didn’t say how…
Mandelbrot’s Fractals
Weirdly enough, it’s much easier to imagine a bent torus for which acceleration is undefinable everywhere.
To understand what that could mean, let’s look at some other sick geometrical objects: Non-differentiable continuous curves.
First examples of such curves were given in the 19th century. They were called monsters. I guess that, Historically, one of the first examples of a monster was that of the function $\sum 2^{-n} cos(4^n x)$. But the more popular example nowadays is the Koch snowflake, as beautifully explained in the awesome show Fractals – The Hidden Dimension by NOVA. Or, even better, the curve formed by the British coastline:
Exactly! And it took another genius to unveil the magic of fractal geometry. This genius is Benoît Mandelbrot.
Curiously though, Mandelbrot’s ideas weren’t popular at first. His first papers on this new kind of geometry were so unusual that the mathematical community rejected them. Referees claimed that the papers, despite displaying pretty images, did not contain actual mathematics. Because the community was not ready for his new ideas, Mandelbrot decided to write a book on his own. This best-seller was so amazing that it quickly became iconic, not just for young mathematicians, but in popular culture as well!
Now, the thing with fractals is that it’s very easy to make a shape of any length. For instance, you can draw a “curve” that looks exactly like a circle, but actually has a length of 4. This is what Vihart did in this awesome video:
So, following Mandelbrot’s (and Vihart’s) ideas, it’s not too hard to imagine a torus whose lengths perfectly match that of the Netwalk world. In other words, through a fractal process, it’s (at least theoretically) possible to describe a simple procedure to fold the square of the Netwalk world into an origami torus-like “zigfinihedron” which glues opposite sides.
Look carefully… The Hévéa Torus is not a zigfinihedron! What the Hévéa team was searching for was a smoother bending of the torus, which, although had no second derivatives, still had continuous tangent planes at all points! And the trouble of fractals is that they are precisely rough objects with no such continuous tangent planes…
Somehow we need a trade off, between the smoothness of classical surfaces and the roughness of fractals. This trade off is what the Hévéa team called smooth fractals.
The Hévéa Torus
The idea of smooth fractals isn’t far from what was hinted at by John Nash. His embedding theorem stated that if a manifold could be topologically embedded in a higher dimension space, as we have done it for the Netwalk world, then this embedding could be smoothly corrugated like Vihart’s zigfinigons to end up isometric, while having tangent planes at all points. What’s more, Nash proved that the amplitudes of the corrugations could be as small as we wanted.
So, following Nash and Mandelbrot’s ideas, the Hévéa team has added several layers of corrugation to a classical torus embedding. This is what’s illustrated below, where the 3 first layers have been added sequentially:
Let’s have a closer look!
Just like Vihart’s drawings, the Hévéa Torus is theoretically obtained by adding an infinite amount of such corrugations. But, computationally, the Hévéa team merely added 5 layers, as any greater layer would in fact be imperceptible given the resolution of the image.
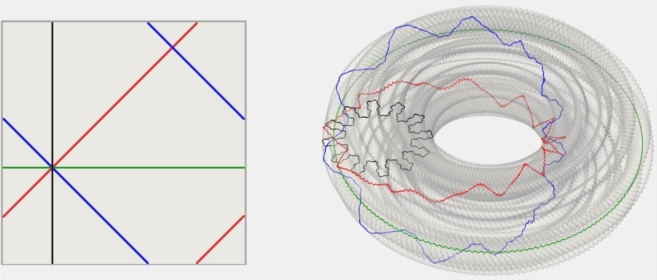
That’s hard to verify… but yes. Below is an image which displays the correspondence between lines in the Netwalk world and lines in the Hévéa Torus:
Amazingly, the black and green loops actually have the same lengths in both figures. Granted, it’s a bit less obvious on the Hévéa Torus, but that’s because the black loop has a more fractal-like structure, which makes it longer than it seems to be!
Yes! The key to obtain the smoothness of our corrugated torus is to have the amplitudes of successive corrugations decreasing faster than their “wavelengths”. By opposition, Vihart’s drawings had rather one-to-one ratios. For instance, at 3:50, she divided amplitudes of corrugations of her curves by 2 while she made twice many of them. Instead, by carefully adjusting the faster decrease of amplitudes of successive corrugations, the Hévéa team managed to guarantee the $\mathcal C^1$ continuity of the Hévéa Torus!
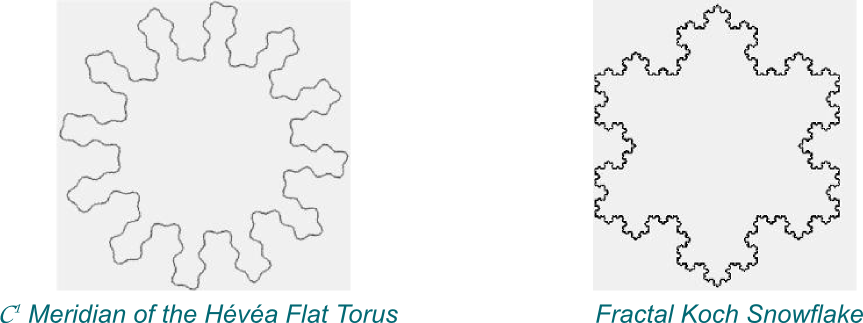
One way to see that is to take the shape of the black loop of the figure above (which corresponds to a meridian), in the 3D space the Hévéa Torus is embedded in. Let’s compare that to a Koch snowflake.
Importantly, as opposed to the non-differentiable Koch snowflake, the meridian of the Hévéa Torus is still smooth enough to have (continuous) tangents at all points.
Let’s Conclude
Instead of recapitulating, I’ll let the great James Grime sum up all we’ve discussed here:
Now, the result of the Hévéa project is a spectacular achievement of over 160 years of mathematical pondering. Obviously, this article only mentions the few mathematicians who made the most stunning breakthroughs in this investigation. But, unfortunately, it also dramatically fails to account for the hundreds of other mathematicians who have shaped and reshaped our intuitions of curves and surfaces, in a deeper but less obvious fashion. For me, this amazing silent build up is the source of the magic of mathematics. Think about it. Thanks to many unsung mathematicians, we now have in front of our eyes an object that the great Gauss, Riemann, Nash and Mandelbrot couldn’t even imagine, even though they had been searching for it all along. I hope you feel privileged and dismayed by the following precious images of the Hévéa Torus…
I should say that even though combining Nash and Mandelbrot’s ideas sound reasonably doable, it is actually a huge and difficult endeavor. Once again, the Hévéa team had to spend 5 years to come up with the Hévéa Torus, after several unsuccessful attempts. It was a tedious and tricky work, which involved very modern mathematics, including and especially Mikhaïl Gromov’s homotopy principle. This gives me one last occasion to stress how big an achievement the conception of the Hévéa Torus is. Congrats to the Hévéa team!
Let me leave you with my favorite image of the Hévéa Torus, taken from its interior, with light coming from the opposite side… Astonishing!
One last thought… Can you believe that cutting through the Hévéa Torus twice yields a square?









Leave a Reply