Although not totally right, it’s often written that social interactions are what make humans very different from animals. In fact, Joel Brown, a renowned professor in ecology, once told me that, as a result, game theory ruled our every day’s lives. While naive people play games they are not aware of, paranoid people imagine themselves playing a game when they are not. The movie “A Beautiful Mind” displays how the great American mathematician John Nash overcame an sickness which made him belong to the latter sort of people. But that’s not what John Nash is famous for. In the middle of the 20th century, his beautiful mind brought major concepts to the emerging game theory, first defined for nil-sum games and then extended to cooperative games by John von Neumann and Oskar Morgenstein. Game theory is nowadays, 50 years later, an incredibly dynamic field of research.
I’ll present some of the major concepts of game theory through classical examples of games. More advanced concepts including extensive form, Stackelberg games, mechanism design, evolutionary game theory and mean field games are dealt with in my article on advanced game theory. However, I’m not going to detail these concepts a lot in this article. So I’m counting on you to write other more detailed articles on these concepts for more accurate understanding of them.
Split or Steal
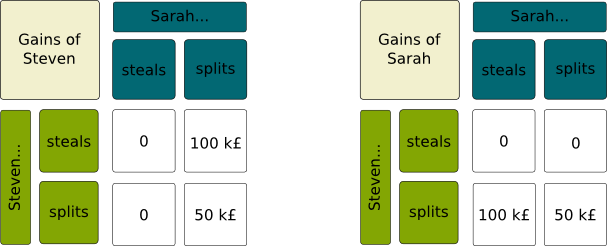
Split or Steal is the ending part of a British TV game show. The two contestants are faced with a certain amount of money. Each of them needs to decide whether to split this amount or to steal it. The choice is made without the contestant’s knowledge. If both steal, then the money is given to no one. If one steals and the other splits, then the money goes all to the stealer. If both split it, they each get half of the money. The following video displays an extract from the show.
The contestants are commonly called players or agents. Here, each player can choose to split or steal. These are his possible actions. In the game, there are 2 possible actions for each player. Since the game involves 2 players and is finite (that is, for each player, the number of possible actions is finite), it can be described with two matrices, called payoff matrices, which displays the gains (or payoffs) of each player. These games with 2 players and finite sets of actions are called bimatrix games. Below are displayed the two payoff matrices.
Notice that, for each player, no matter which action the other chooses, one action is always better than the other. We say that playing this better action is a dominant strategy. It’s the case of stealing in the Split or Steal game. As a result, if there is no cooperation and if each player is selfish, they will both play the dominant strategy. Yet, each player would prefer that the other plays the dominated strategy. In our case, each player is hoping that the other will split. Thus, any rational player has incentive to act like he’s going to cooperate to encourage the other to cooperate too, but eventually, if the action can be made secretly from the other, he should not cooperate.
In the TV show, there is also a matter of ethics linked to honesty, which may lead players to split. Also, winning half the total still sounds like winning, maybe even more, for some people, than actually winning the total. These two remarks can be summed up by saying that the gain of the players cannot be reduced to the financial gain, and it can be modeled by taking into account other factors in the actual gains. Another explanation may lie in the fact that players have not made all of our reasoning…
The Prisoner’s Dilemma
The Prisoner’s Dilemma is the most famous example of Game Theory, stated in 1950. Herminio Lopez gave an illustration in soccer tournaments. Check the great following video by Instant Egghead to understand it well.
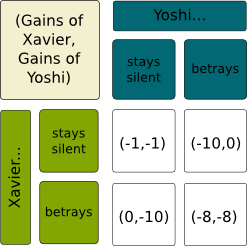
Basically, two suspects who cannot communicate can denounce each other. If they do denounce, their penalty is diminished. But if they are denounced, they get a big penalty. The following table displays the payoffs corresponding to the example of the video (except that I have replaced 1 month by 1 year for simplicity of notations). Note that I have merged the two payoff matrices into an array. This is the most common representation of 2-player games with finite sets of actions.
Just like in Split or Steal, we can notice that betraying is the dominant strategy, even though it’s not the one the other player hopes will be played. Because betraying is dominant, the strategy profile where both betray is a Nash Equilibrium.
A Nash Equilibrium is a strategy profile such that, for each player, assuming that others will play accordingly to the strategy profile, there is no better strategy than playing according to the strategy profile. Equivalently, no player has incentive to deviate unilaterally from the strategy profile. As a result, if players make a deal to play a Nash Equilibrium, and if, after that, each player plays secretly without communication, then you can be confident that they will all follow the deal. Indeed, each of them, assuming that others follow the deal, has incentive to follow the deal.
You are right! But there’s actually more: If each player has one strictly dominant strategy (that is, always strictly better than all other strategies), then the strategy profile where all play their dominant strategies is the only Nash Equilibrium. Indeed, no matter what others do, it is always better to play the strictly dominant strategy.
Not always… This article indicates that prisoners do play it half of the time. What’s particularly amusing is to see that students play it much more often, which sort of indicates that the moral of cooperation is much stronger for prisoners than students! A factor which may explain that is the fact that this game is repeated, in the sense that you’ll still have to face the other prisoners or students the next days…
Well, that’d be too easy… Quite often, there is no dominant strategy. Just like in the battle of sexes.
Battle of the Sexes
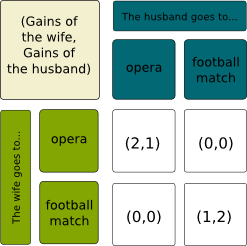
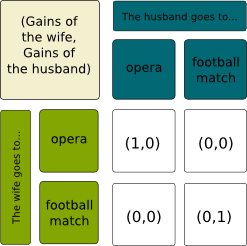
The battle of the sexes is a classical example of the more general case of coordination games. Imagine a married couple who needs to decide what to do in the evening. The wife has mentioned the opera, while the husband has suggested the football match. However, their cellphones have run out of battery and they cannot communicate. They each have to decide where to go. Obviously each prefers the place he has proposed, but both prefer being with the other than anything else. Here is the payoff matrix.
Exactly! However, there are two Nash Equilibria here…
Indeed. If the wife and husband agree to go to the opera, and therefore expect the other to go there, then there is no better strategy for them than actually going there. Therefore, the strategy profile where they both go to the opera is a Nash Equilibrium. Similarly, the case where they both go to the football match is also a Nash Equilibrium.
Especially if, with time, the couple’s desire to spend the evening together decreases (I hope it won’t be the case for you!). By subtracting 1 to the gains when they are together, we now have the following payoff matrices:
The Nash Equilibria would still remain Nash Equilibria, but there will no longer be strict Nash Equilibria. As a matter of fact, knowing that his wife will go to the opera, even though there is no better strategy for the man than going to the opera, going to the opera is not strictly better than going to the football match. In fact, going to the football match is for him a dominant strategy. But if both players play their dominant strategy, then we also have a Nash Equilibrium. Every case of the table is now a Nash Equilibrium.
That’s where comes the concept of correlated equilibrium. For a correlated equilibrium, players take into account an external signal that hints them at playing a specific strategy. Now, given his signal, each player can assume which signal the other may have with a certain probabilistic distribution but he does not know the other’s signal for sure. If, given the probabilistic distribution of signals for the other, each player still has incentive to follow the hint of the signal, then the signal system forms a correlated equilibrium.
Applying this in our example is rather easy: the couple may flip a coin. Head is the opera, tail is the football match, for instance. As a result, in means, if they do that every week, they’ll both be happy and equally happy. Here I’m just having an overview of correlated equilibria… Don’t hesitate to a write your own article on this concept!
Cooperative Games
What all the examples we have seen so far show is that…
Indeed. That’s why game theorists like to think about what could happen if players actually cooperated. The problem is that, in the games we gave mentioned, by cooperating, they lose something by not deviating from the cooperation. We often need to compensate them by reallocating the gains of the cooperation. This reallocation, called solution concept, can be crucial and hard to be done. That’s where comes cooperative games theory, as opposed to non-cooperative game theory we have studied so far.
The major concept in cooperative games is the Shapley value, introduced by Nobel prize winner Lloyd Shapley. It gives a fair-enough way to reallocate the gains. Its idea is to allocate to each person the means of what he gives to any coalition he would enter, with more important weights to larger coalitions. The Shapley value is interesting because it yields several properties (efficiency, symmetry, additivity, zero player). I give a more complete definition of the Shapley value in my article on fair division.
Yes! But the Shapley value also has flaws. Mainly, it is not necessarily a Nash Equilibrium, as it’s possible that players still have incentives to get out of the coalition. Consider Split or Steal for instance. A cooperation game would lead to the both players winning together all of the sum and then sharing it equitably. It’s still better to steal the money…
More generally, it’s also possible that a subset of players would have incentives to get out of the grand coalition, that is the coalition with all players. That’s the case in the example of miners. Suppose there are three of them, but there only needs to be two of them going the mine and bringing back all of its gold. If only one goes, he won’t be able to bring back anything. A Shapley value would get all miners going to the mine and splitting the booty in three equal shares. But two of the miners would have incentive to go to the mine without the third one, hence sharing the booty in two equal shares. In cooperative game theory, we say that the grand coalition and the solution concept are not stable. Many researches focus on the set of stable solution concepts for the grand coalition is called the core. However, this core is generally hard to study and it might be empty. These concepts have other flaws that I mention in my article on fair division.
The concept of the core is close to another concepts in non-cooperative games: the concept of strong Nash Equilibrium. Recall that a Nash Equilibrium is a strategy profile such that no player has incentive to deviate from unilaterally. Now, a strong Nash Equilibrium is a strategy profile such that any subset of players has no incentive to deviate from collectively.
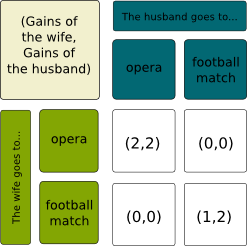
Sure! Let’s consider again the initial battle of sexes. However, this time, we assume that the husband has taken lessons of musics and he now enjoys the opera just as much as football. We may now have the following payoff matrices:
In this case, even though it is still a Nash Equilibrium, the strategy profile where both go to the football match is not a strong Nash Equilibrium. As a matter of fact, if the couple collectively deviates from the bottom right case to the top left case, then they will both be at least as happy, and one of them will be strictly happier.
Yes. Any strong Nash Equilibrium is a Nash Equilibrium but the inverse is not necessarily true.
Cournot Competition
It’s time for you to learn about the first major application of game theory. Designed by the French mathematician Antoine Augustin Cournot in the middle of the 19th century, the Cournot competition illustrates how competition yields a decrease of prices. More precisely, it displays the fallouts of duopoly as opposed to monopoly. I’m not going to explain it in details though. You are more than welcome to write an article on the topic!
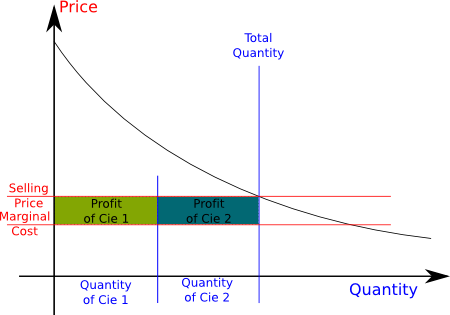
In the Cournot competition, two companies produce the same good. They each choose a quantity to produce. This choice is their action. We shall notice that the set of actions here is infinite. Now, depending on the total produced quantity and the demand curve, a price is given. Each company’s profit is the product of his production by the difference between the price and the marginal cost (the cost of producing one unit of product). The objective of each company is the maximization of its profits.
In the figure, company 1 chooses the quantity of Cie 1, while company 2 chooses the quantity of Cie 2, as they each try to maximize their profits, which is the area of the green and blue rectangles.
It’s important to notice that each company’s best choice of the quantity to produce depend on the other company’s choice. If the other company produces a lot, then the prices will be low, and producing a lot can lead to negative profits. But if the other company does not produce a lot, there is an incentive to produce a lot, knowing that the prices will remain high enough. We call the best choice of a company given the other company’s choice a best response to the other company’s strategy. Notice that a Nash Equilibrium can be defined as a strategy profile such that any player’s strategy is a best response to the other company’s strategies.
The problem can be solved in simple models where the demand is linear and the marginal cost is constant. It can be shown that, at the Nash Equilibrium, the total production is higher than if a single company was producing to maximize its profits. As a result, the prices are lower. Although simple, this illustration has been the basis of many reasonings of economists.
Princess and Monster
I am now going to present very briefly a more complicated game called Princess and Monster, which will help us introduce another major concept in game theory. This game is a specific case of the more general case of pursuit-evasion games. Let’s consider the classical game of Nintendo, where the Monster Bowser is pursuing the Princess Peach, who must be saved by the Italian plomber Mario.
Now, Princess and Monster consists in Bowser chasing Peach in a given bounded room. But the trick is that the light is off. Although they both know what the room is like, they have no idea where the other is. Now, Bowser has to find Peach as soon as possible, because, for instance, he knows that Mario can arrive at any time. In this set, if Peach’s run in the room is known by Bowser, then Bowser’s strategy can be chosen accordingly. Similarly, if Bowser’s run is deterministic, Peach can run accordingly. But if Peach chooses her run randomly, Bowser will have to adapt his run to minimize the expected time of capture, which will give him more trouble. The same reasoning can be done for Peach.
First, this is a particularly common assumption, especially if you consider that players play repeatedly. Eventually, they know what strategy the other is playing. But mainly, the concepts of best response and Nash Equilibria involve knowing the other player’s strategy.
Introduced by Rufus Isaacs in 1965, the Princess and Monster problem had been open problem for more than a decade, until it was solved by Shmuel Gal in the late 1970s. As expected, the Nash Equilibrium consists in players choosing their run randomly. Such strategies are called mixed strategies, by opposition to pure strategies, for which actions are chosen deterministically. The mixed strategy is therefore a mixture of pure strategy with different probabilities of playing each of the pure strategy.
Obviously, it depends on the characteristics of the room and of the players. But, according to Wikipedia, Nash Equilibria all have the following feature: Peach’s strategy at equilibrium is to run to some randomly chosen location in the room and stay for a while. And repeat this procedure indefinitely. I’m not very familiar with pursuit-evasion and search games. Your help, by writing an article for instance, is more than welcome!
Rock Paper Scissors
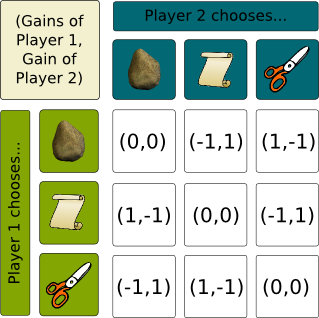
Rock Paper Scissors is a very basic popular 2-player game. Each player chooses Rock, Paper or Scissors, knowing that Paper covers Rock, Scissors cuts Paper and Rock crushes Scissors. This gives us the following payoff matrices:
Let’s search for Nash Equilibria…
Exactly. In any case, one of the players is not winning. Yet, for any case, players can deviate and get a winning case.
Actually there is, according to Nash’s theorem. This is one of the shortest major theorem I know: Any finite game has a mixed-strategy Nash Equilibrium. The proof involves a fixed point theorem, but it’s way too complicated for me to dwell on here. Let’s just trust John Nash.
Exactly. And we’d find that the equilibrium is for both players to play uniformly randomly one of the three pure strategies. If the other player does that, then doing that too, just like playing any strategy, would yield an nil expected payoff. Thus, there is no better response than the mixed strategy we have described, and it is therefore a best response to itself, which proves that it’s a Nash Equilibrium.
In fact, two other properties of Rock Paper Scissors would have led us to concluding to the existence of a mixed strategy which yields a nil expected payoff for both players. The first property to notice is that it is a nil-sum game, that is, whatever player 1 wins, player 2 loses it. Equivalently, and it’s easy to see on the table, their gains always sum up to 0. The minimax theorem by John von Neumann in 1928, tells us that, for any nil-sum game, the best one player can get by announcing his strategy first is equal to the best he can get by reacting to a smart opponent’s strategy. As a result, nil-sum games all have Nash Equilibria, which all yield the same expected gains for player 1, as well as the same expected gains for player 2. There is much more to say, and you are welcome to do so!
The second property is the symmetry: The rules are the same for both players. This can be observed in the payment matrices. The transpose of player 2’s payoff matrix is equal to player 1’s payoff matrix. As a result, the payoffs at a Nash Equilibrium of both players must be the same. Since it’s a nil-sum game, their payoffs must also add up to 0. Thus, their payoffs are necessarily 0.
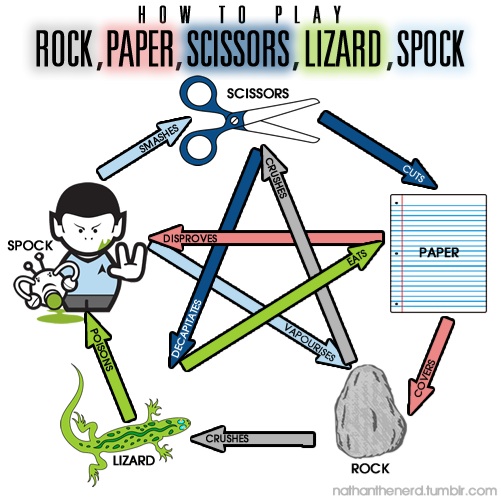
For the fun of it, I’ll mention that one flaw of this game is the relatively frequent occurrence of equalities when playing Nash Equilibria. That’s one thing that Rock Paper Scissors Lizard Spock corrects:
The Nash Equilibrium is still playing one of the action uniformly randomly, because of the symmetry between the different actions, which can be noticed in the following figure:
Rock Paper Scissors is very interesting for the study of Evolutionary Stable Strategies. Find out more in this article.
Let’s sum up
Game theory is a very large field and we have barely scratched its surface. I hope this read has interested you, and if it has, I can only encourage you to read more about it. For a start, please read my overview of advanced game theory. Or check the applications of game theory to predictions in geopolitics by the mind-blowing Bruce Bueno de Mesquita.