We saw in our post on Euclidean Geometry and Navigation how Euclidean geometry – geometry that is useful for making calculations on a flat surface – is not sufficient for studying a spherical surface. One difference between the two is that on a flat surface, two parallel lines, if extended indefinitely, will never meet – this can’t be proven, but is considered an assumption of Euclidean geometry. On a sphere, however, if two parallel lines – great circles – are extended, they will end up intersecting. So spherical geometry, and basic facts about navigation on a sphere such as the Earth, is fundamentally different from Euclidean geometry, or geometry on a flat surface. One consequence of the fundamental difference between flat surfaces and spherical surfaces, such as the Earth, is that any planar depiction of the Earth – such as a map on the wall, in an atlas, or on Google Maps – will necessarily have some distortions.
The impossibility of making perfect maps
A first example: The Mercator projection and flight routes
Take a look at the following depiction of flight routes between major cities around the planet:
You probably notice that the direct route from, say, London to New York, is not a straight line on this map – it in fact appears to be curved, even though when you fly from London to New York, you fly more or less directly from origin to destination – you fly on what we previously defined as a “great circle”. Here’s a NASA picture of the Earth as seen from outer space that should clarify this:
Notice here that a direct flight between New York (on the left) and London will pass over the north Atlantic, close to Greenland (in the middle top of the picture). On the map given above, however, if we draw this path out, it looks like the plane is curving to the north when it flies over the north Atlantic.
This is a perfect illustration of the fact that spherical geometry and Euclidean/flat geometry are fundamentally different. When we try to make a flat map of the Earth, we will always make distortions, so a direct flight from London to New York actually appears to be curved when we draw it on a map. The fact that the surface of the sphere and a flat surface are geometrically distinct is a consequence of the “Remarkable Theorem” discovered by the prolific German mathematician Karl Gauss.
Gauss’s “Remarkable Theorem” shows that we can show that the Earth is not a flat surface simply by taking measurements on its surface – in other words, without studying the Earth from the space in which it lies. The “Remarkable Theorem” is described as remarkable for this reason – it suggests that we can completely understand an object’s curvature in space (“Gaussian Curvature” in mathematical terms) simply by taking measurements on the object’s surface. We’ll come back to this point in our third post on Einstein’s theory of general relativity. Also, be sure to check out Le’s article on Topology, a related field which also studies the structure of objects in various spaces, but with less emphasis on precise measure and more emphasis instead on their fundamental shape.
The “Orange Peel” Experiment
Here’s another way to think about the issue of making maps. You can even do this at home. First, take an orange and draw decent outlines of the continents on it. Then carefully peel the orange, and flatten it on a surface.
No matter how you try to flatten the orange, you always end up distorting some parts of the “map” you have drawn on it. As you play around with this, you can probably figure out ways to flatten the orange peel while keeping some areas of the map intact, but invariably as you do this, other parts of the map will be distorted.
Three types of map projections
So here we arrive at a practical problem for cartographers – people whose job is to make accurate maps, for a variety of purposes. Their job is to depict the Earth – a spherical object – as a flat surface, and this necessarily results in distortions. The process of depicting the spherical surface of the Earth on a flat map is known as projection, and there exist a number of different methods of projection, each with its own distinct advantages and flaws. For example, certain projections accurately portray respective areas of different places on the globe, but distort the distances between places. Such a projection might be useful for someone interested in the respective size of places, such as a population specialist, but would not be useful for someone trying to plan a journey between places.
The Mercator Projection
The map of the plane routes above, as well as Google Maps, uses what’s known as the Mercator Projection, invented by a Flemish cartographer in 1569. Here’s another, full view of the map obtained using the Mercator Projection:
In the Mercator projection, the area of places far from the equator is heavily distorted. For example, Antarctica appears to be the largest continent on this map, when in fact it is the 5th largest continent, and Alaska appears to be the same size as Brazil, when it fact its area is around a fifth of that of Brazil. Still, the Mercator projection is useful for such maps because it projects areas very accurately on a small scale – this is why when you zoom in on a city in Google Maps, what you see is a very accurate representation of the actual city.
The Galls-Peters Projection
Let’s look at a second example of a map projection, the Gall-Peters projection. The earliest form of this projection was originally developed by a 19th century Scottish clergyman named James Gall. He wanted a map that would be useful for astronomical calculations – specifically, he needed a map projection that would accurately depict areas on the surface of the Earth – the commonly used Mercator Projection significantly distorts areas on the surface of the Earth. Here’s the map that he developed:
“GALL’S ORTHOGRAPHIC PROJECTION
EQUAL AREA. PERFECT.”
For Physical Maps, chiefly Statistical.
from www.heliheyn.de
This map – and an equivalent map developed in 1967 by Arlo Peters, turned out to be politically controversial as a map, since it gives an accurate sense of the size countries lying near the equator – such as African nations which have faced considerable poverty and political instability. The Mercator projection, on the other hand, makes these countries appear small in comparison with countries such as those in Europe. The Gall-Peters Projection, therefore, has been used by aid organizations and other groups concerned with social or political equality in Africa.
Check out this clip from the series “The West Wing” regarding the Gall-Peters projection map. Note that the clip describes the projection as the Peters projection, even though it was first developed by James Gall, but reintroduced and popularized by Arlo Peters.
Shortest-Route Projection
Let’s take a quick look at two other types of projections, in order to emphasize the different possible ways to project the Earth’s surface onto a flat map, and how this necessarily results in distortion. We’ve seen the Mercator projection, which is the most widely used map projection. This projection gives an accurate representation of relatively small areas, particularly close to the equator, but also distorts areas far from the equator so that they appear bigger than they actually area. The Gall-Peters projection gives an accurate representation of the respective areas of countries and continents, but distorts the apparent distances between various places.
A third type of projection, known as a shortest-route projection, yields maps that accurately portrays the shortest route between a given, central location, and other places on the planet. An example of a shortest-route projection is the family of projections known as the Azimuthal projections, an example of which can be seen here:
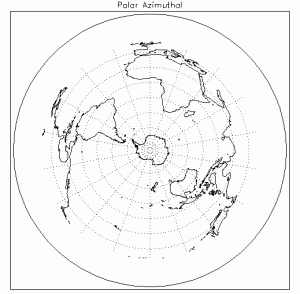
An Azimuthal projection gives an accurate idea of the shortest route from the center point on the map to any other point on the surface of the Earth (in this map, it is located at the south pole), but, as you can probably see, also distorts the area of places far from the center of the map.
Another example of a shortest-route projection is the Gnomonic Projection, seen here:
The Gnomonic Projection can be created by taking a see-through globe, placing a light at the center of it, and shining the light on a surface. The outline of the continents on the globe will appear on the surface, as in the picture above.
To summarize:
We’ve explored the fact that the geometry of a sphere and the geometry of a flat surface are fundamentally different by looking at a number of different ways to project the continents of the Earth onto a map. Each method of projecting the Earth’s surface onto a flat map has inherent distortions, but projections can be designed so that they also have properties useful for various purposes such as designing a flight route, comparing areas of different countries, or finding the shortest route between two points on the Earth. What we haven’t done is look into the mathematics behind each of these projections, as this would require a more complicated level of mathematics. If you’re interested in exploring the mathematics behind each of these projections, I’ve included some links below. In the next post, we’ll be looking at how the ideas we’ve been discussing here were developed into a mathematical framework which Einstein used to develop his general theory of relativity, which describes the geometry of space-time.




Awesome article, Scott! It reminds me that once I took a flight from Montreal to Beijing and I was wondering whether it’d go east or west. As it turned out it went through the North Pole!
Maps are so misleading, it’s nice to point it out. Another example is upside down maps (http://flourish.org/upsidedownmap/hobodyer-large.jpg), in which Northern countries also look very small!