Space deformations play a key role in our understanding of the Universe. Modeling them mathematically has enabled major breakthroughs in physics and chemistry. Amusingly, as they were studied, they have also led to major advancements in mathematics too, as they correspond to great representations of more complex abstract structures known as groups. In this article, I’ll give you an introduction to the idea of group representation which has revolutionized 20th century pure mathematics.
Space Deformation
Humm… I’ll get to this. But first, let’s talk about space deformations. Look at this moray eel, and imagine it turning its head to the left.
Any turn of the eel’s head corresponds to a space deformation. The set of all space deformations we obtain this way corresponds to all rotations of space.
Indeed. Yet, weirdly enough, the greatest breakthroughs of physics comes from the very understanding of how space gets changed based on who and how it is observed. This is true for Galileo’s inertial system, Newton’s first law, Einstein’s special and general relativity, quantum mechanics or black hole theory. And the relevancy of studying space deformation is due to the fact that switching from a viewpoint to another can be thought exactly like a space deformation.
Yes, thanks to the awesomeness of mathematics. How can mathematics make us understand space deformations in complicated spaces? Well, in many fields of mathematics which study deformation of mathematical objects, it is crucial to find something that still characterize deformed objects, no matter which space deformation is applied. We call this constant characteristic an invariant.
In the case of space deformation due to the eel’s turning its head, the most crucial invariant which characterizes these deformations is the invariance of distances. The distance between two fishes remains the same whether the eel turns its head or not! Another important invariant is the invariance of the concepts of left and right, namely if you deform space by turning your head, what was the left for someone remains its left. Mathematically, these two invariants characterize the set of rotations. This set is so important that it has its specific notation, namely $SO(3)$. Even though they might not be aware of it, $SO(3)$ is the group that Galileo and Newton have been using all along. And then came Einstein…
In 1905, Einstein imagined that space could also be contracted by the motion of the observer! This means that he postulated that distances were no longer an invariant of Nature! Instead, based on observations such as the Michelson-Morley experiment results, he claimed that the speed of light was an invariant. This implies that, when space gets contracted, time gets dilated accordingly so that the speed of light remains constant. To understand this, Einstein had the great idea of considering spacetime as a single entity which was deformed by motions. In this setting, the invariance of the speed of light could be translated into the invariance of a quantity known as the spacetime interval. All spacetime deformations which preserve the spacetime interval are known as the Lorentz group, denoted $O(1,3)$. The 1 stands for time, and the 3 for space.
Yes! Just like for the rotational group, the orientation of space is conserved. As a result, we say that deformations are proper. And there’s a last important invariant, which is the invariance of the direction of time. Indeed, as far as we know, time always go towards the future for all observers, at least as long as we don’t exceed the speed of light. This is the orthochronous property. These three invariants fully described all spacetime deformations due to motions in Einstein’s special relativity theory. This major group of spacetime deformations is known as the restricted Lorentz group and is denoted $SO^+(1,3)$. With what I’ve said, you might now better understand this great video from Minute Physics:
Yes! How amazing is that? You can learn more by reading my article on spacetime of special relativity.
Yes, but not the kind of space deformation we’re describing in this article! In order to describe groups, the only deformation of space we are interested in are those which transform lines into lines. In the spacetime of special relativity, a “line” in spacetime corresponds to a motion at constant speed. So deformations in this space must transform motions at constant speed to motions constant speed. Such deformations are called invertible linear transformations, mathematical better known as linear automorphisms. Together, these deformations form the general linear group, quite often denoted $GL$.
The Alternating Group
Let’s now get to group representations! Maybe I should define what is meant by group first…
The concept of groups is probably one of the most abstract in mathematics. Roughly said, a group is an abstract collection of objects which combine nicely with each other.
A great example of groups is the set of symmetries, as you can read it in this article of mine. But there are plenty of other major groups, like Lorentz’s group. Another more popular example is the set of moves you can do to the Rubik’s cube. In this article, let’s focus on the alternating group of degree 3, denoted $A_3$.
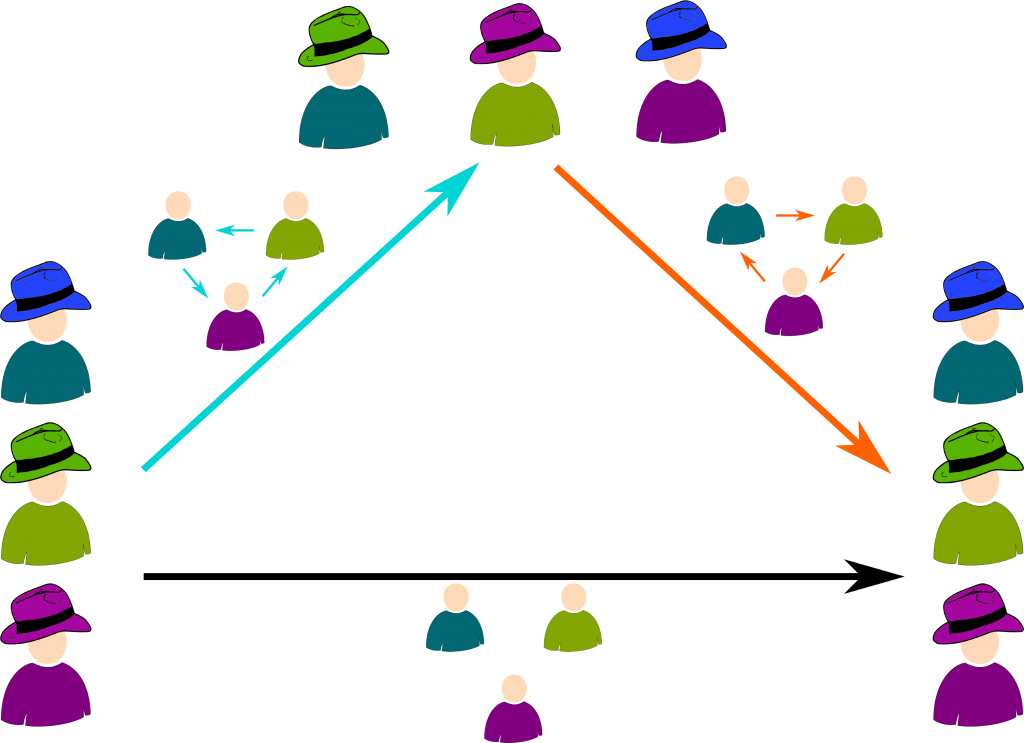
Consider three guys with three hats, as in the following figure:
Now, the three guys can trade their hats. Each trade is called a permutation of hats, and is thus an element of the group of permutations $S_3$. The alternating group of degree 3 is the set of permutation for which either everyone or no one trades. All 3 possible trades are displayed below, where arrows have to be read “gives his hat to”.
For instance, if the cyan trade is carried out, then the blue guy gets the green hat, the purple guy gets the blue hat, and the green guy gets the blue hat.
Yes. Once a trade has happened, we can carry on with another trade. Assume we started with the cyan one, and that we now proceed the orange one. We would then be combining the cyan trade with the orange trade. The operations are displayed below:
Note that the overall operation corresponds to doing nothing. This is the left permutation of the above figure (let’s call it the black trade)! This is major feature of groups: the combination of any two elements of a group is still an element of the group. We say that the combination is a binary operation. Another major property is that we can always go back to the initial position. We say that any element of the group is invertible. Finally, the last property groups must have is called associativity, but I won’t dwell on this here.
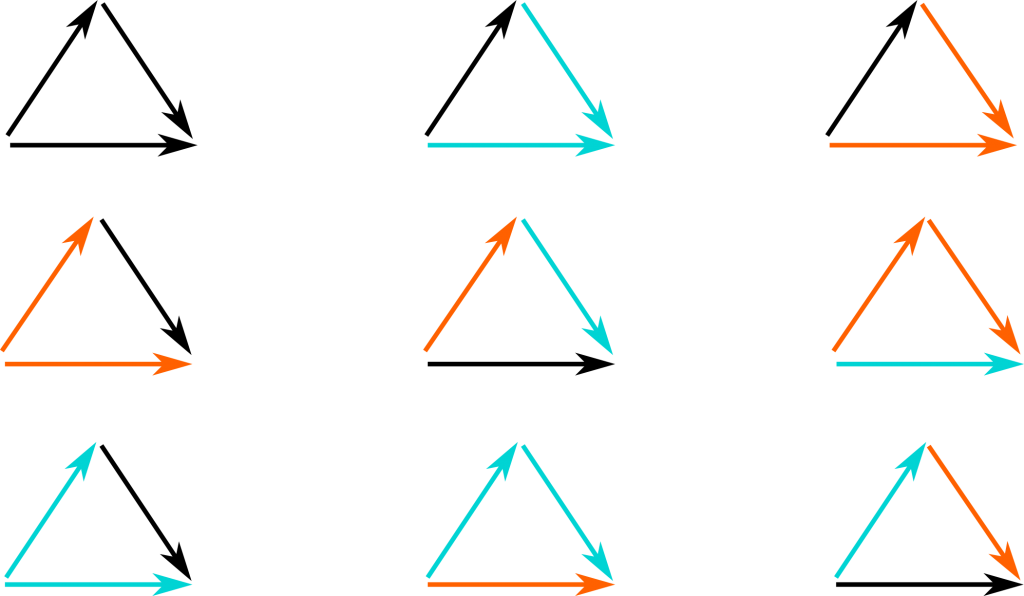
Good question. The following table corresponds to a table of multiplication. The result of the combination of two trades is drawn similarly to the arrows displayed in the previous picture.
Group Representation
A representation of a group is the matching of elements of the group with space deformations. Indeed, what’s great about space deformations is that they form a group! Just like moves on a Rubik’s cube or the trades we have just discussed, space deformations can be sequenced. This corresponds to deforming a deformed space. Also, space deformations can be inverted, which means transformed back to how space was before being deformed.
No, but they can always be matched with space deformations. Such a matching is a group representation.
Not at all. The one thing that’s tremendously important is the fact that the structure of group is conserved by the matching. This means that the space deformation associated to a combination of two elements of a group must be the combination of the two space deformations associated to the two elements. In other words, combinations of elements of the group are matched with combinations of their associated space deformations. This mapping which preserves the group structure is called a morphism.
Well, if I were smart, I could guess one. But since I’m not, let’s use a classical one, called the regular representation. It consists in defining a vector space whose basis vectors correspond to elements of the group. In our case of A3, because there are 3 elements in the group, this corresponds to defining a basis of a 3-dimensional space.
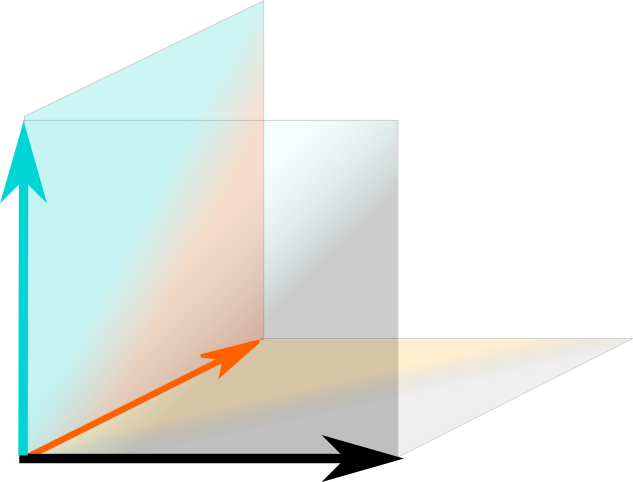
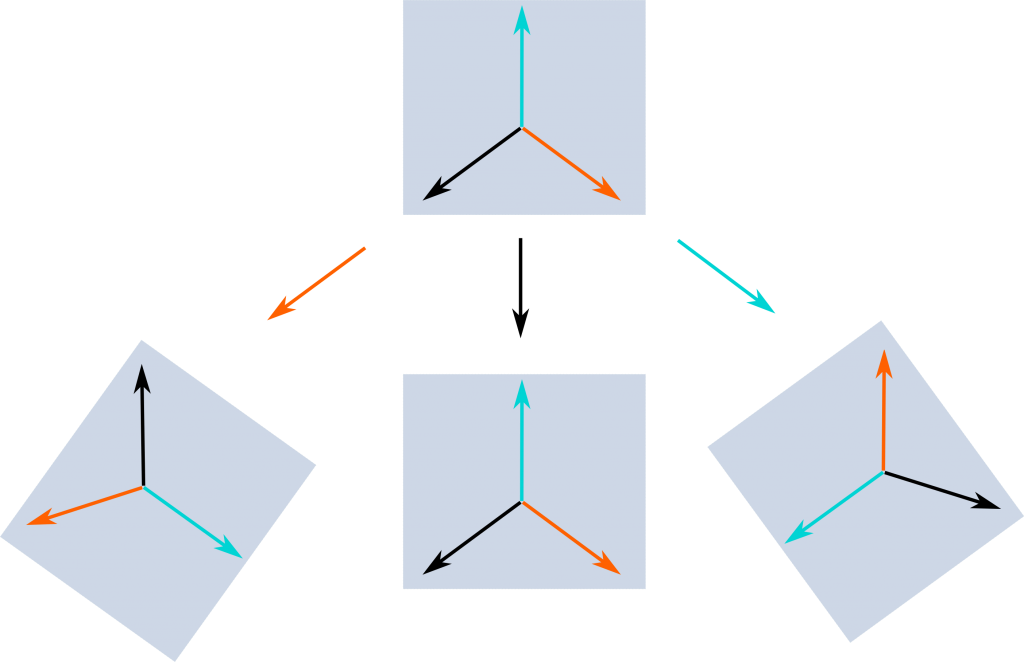
I’m getting there! Consider a trade of hat. When you combine them with another one, you obtain a third one. Thus, the space deformation induced by a trade consists in switching basis vectors accordingly to the result of combining the trade with each trade associated to basis vectors. For instance, the cyan trade corresponds to a space deformation that transforms the orange basis vector by a black basis vector, because the combination of cyan and orange is black. The following figure displays the three space deformations induced by the three elements of the group $A_3$.
Hehe… That’s a great question! The study of simplifying the understanding of a set of deformations is crucial to better understand group representations. The key ingredient to achieve this simplification is to break down space into irreducible spaces.
Irreducible Representation
Let’s get back to Einstein’s spacetime of special relativity. His breakthrough was to imagine that space and time couldn’t be separated. In some sense, this means that spacetime cannot be reduced to space and to time. Considerations of motions imply that spacetime is irreducible.
Yes! In this case, no spacetime deformation transforms space into time, nor time into space. As a result, we can separate them. Space can be studied on its own, and space deformations correspond to rotations. Meanwhile, time is constant.
Hehe. Check the diagonale and its orthogonal plane:
The green diagonale is a stable line since it remains invariant for any of the three space deformations. Similarly, the blue plane, which is orthogonal to the green diagonale, is a stable subspace. As a result, we can break our space into the the green and blue subspaces, and study each subspace separately.
The line surely is irreducible, as it’s the smallest subspace one can think of. We say that it is an irreducible representation of the alternating group. This representation is extremely simple: None of space deformations associated to the group deform it. This representation exists for any group and is called a the trivial group representation. Obviously, it’s not the most interesting one…
Yes. We can project the basis vectors onto the blue plane. The following figure displays what’s happening on this blue plane:
Yes! That’s because they are! What this means is that the group $A_3$ can be represented by rotations of 0, 1 and 2 thirds of a turn, which is a much more visual representation than picturing the trade of hats!
Indeed. Surprisingly though, the understanding of space deformations can be reduced to a few values, known as characters.
Characters
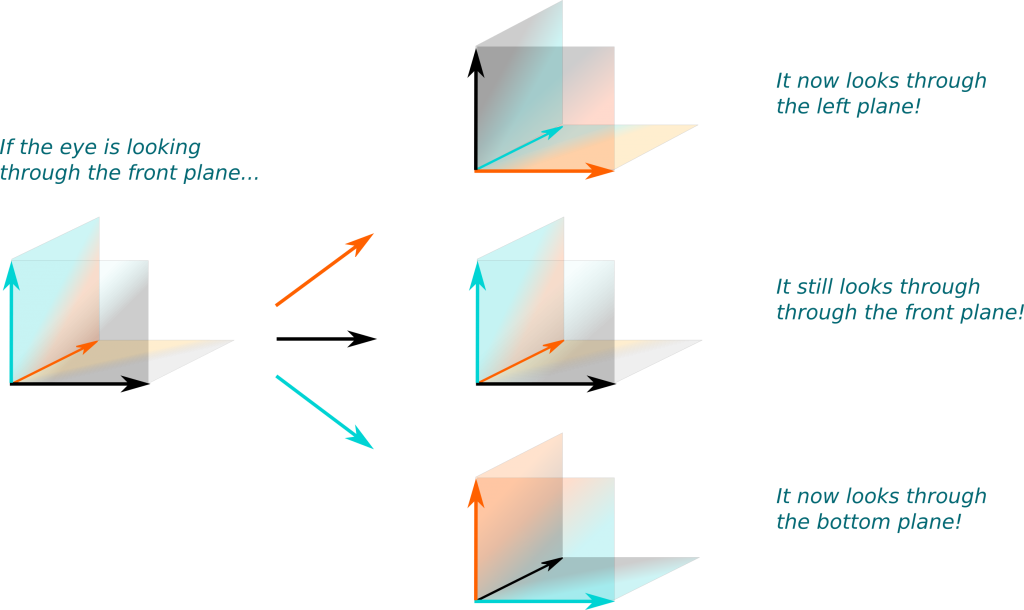
First, I need to introduce a weird but essential construction. For the sake of group representations, it’s relevant to imagine that each basis vector actually creates its own plane!
I know it’s a hard thing to get one’s head around, but we may consider that each basis vector creates a plane around which the vector can rotate and stretch (but not much more). This plane is called the complex plane, and it matches the nice properties of complex numbers. If all basis vectors create their complex planes, we say that the space is a complex vector space. With this construction, our blue stable plane becomes rather a four dimensional real space, as explained in the following video from the series A Walk through Mathematics by researchers and artists from ENS Lyon, France (check the whole series, it’s great!):
I know! It is hard! I’m actively searching for a better visualization of higher dimensional spaces, but the simplest description we seem to have is through the abstractness of algebra…
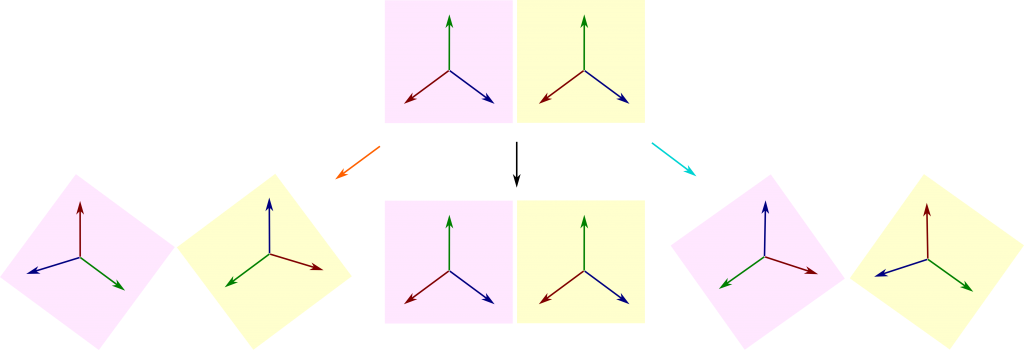
No! It can be decomposed into two complex planes which are stable for all space deformations. On these complex planes, the space deformations still correspond to rotations of 0, 1 or 2 thirds of a turn. But they can now be expressed by a single complex number, respectively 1, $e^{2iπ/3}$ and $e^{4iπ/3}$. This is displayed below, where the two stable complex planes are colored in pink and yellow:
Notice that, on the pink complex plane, the cyan space deformation corresponds to 1 third of a turn clockwise. This means that the cyan space deformation corresponds to multiplying the pink complex plane by $e^{2iπ/3}$. This number is what we call the character of the cyan element of the alternating group for its irreducible representation on the pink complex plane. The character is thus a description of the space deformation on this irreducible subspace by one single complex number. In our setting, this character fully describes the space deformation, but we may in fact consider the character of a space of larger dimension. In this case, the character is a partial description of the space deformation by one single complex number, known as the trace.
Exactly! On the yellow irreducible complex plane, the cyan space deformation corresponds to 2 thirds of a turn clockwise, which means that its character is $e^{4iπ/3}$. For the orange space deformation, it is the other way around, namely a character $e^{4iπ/3}$ on the pink plane, and $e^{2iπ/3}$ on the yellow one. Meanwhile, the black space deformation still modifies nothing, which implies that its characters are 1 and 1.
Yes. Complex planes are always considered irreducible, as multiplying any of its vector by complex numbers generates the whole plane. In particular, since all space deformations leave the green line still, the characters on this plane all equal to 1. Thus, we now have computed all characters of irreducible subspaces of the regular representation.
Surprisingly, yes! This is a consequence of the Frobenius’ theorem proven in 1897, which applies to finite groups. Now, this theorem involves the concept of central functions which would be too long for me to explain here. So let’s only focus on its amazing consequences. One of them is the fact that the regular representation contains all irreducible representations. So, yes, we have computed all irreducible characters! These characters are represented in the following figure, called the character table, which can be considered as a map of the group.
Frobenius’ theorem has other amazing implications! It implies that all representations are made of these irreducible representations. Even more surprising, if we are given the character of a representation only, we can easily find out which irreducible representations make up the representation described by the character. This means that the understanding of a representation can be equivalently reduced to its character!
For finite groups, precisely! And our work is greatly simplified by another corollary of Frobenius’ theorem. Namely, it is a simple calculation to test whether a space is irreducible based on its character. So really, group representation simply boils down to the mere study of irreducible characters!
Let’s Conclude
To recapitulate, we have discussed space deformations and their importance to physics. Then, we showed how relevant they could be for descriptions of groups. We have then explained how the complexity of space deformations could be simplified into the the study of stable subspaces, and, eventually, irreducible subspaces. Finally, we have shown how the simpler idea of characters can provide all the information about representations.
As said in the introduction, group representations are essential for the understanding of some groups which are so abstract that there are barely other ways to think about them than through their characters. In particular, the tremendous work of classifying finite groups has involved a great understanding of group representations. Basically, finite groups can all be divided into simple groups, just like numbers can be divided into primes. Thus, we only need to understand and classify simple groups to understand and classify all groups.
Yes! This classification is now summarized in a few thousand pages that nobody understands entirely. As it turns out, there are only a few classes of simple groups, namely those constructed by prime numbers, the alternating groups of all degrees higher than 5, a few other classes of groups, and 26 other isolated groups, called the sporadic groups. While physicists were chasing elementary particles, pure algebraists were searching for these sporadic groups all along the 20th century to complete the classification. In 1982, their quest ended: Fischer and Griess finally constructed the last and largest of these sporadic groups. This Monster Group (that’s its name!) contains about $10^{54}$ elements! And none of this could have been done if it weren’t for its representation in a space of dimension 196,883, which greatly simplifies it. This space is its smallest irreducible representation!
Obviously, no. For one thing, they now have to face infinite groups. And, in this quest, group representations still have a major role to play. In fact, Andrew Wiles’ proof of Fermat’s last theorem done in 1994 involves the use of several complex groups which can only be manipulated through their group representations!




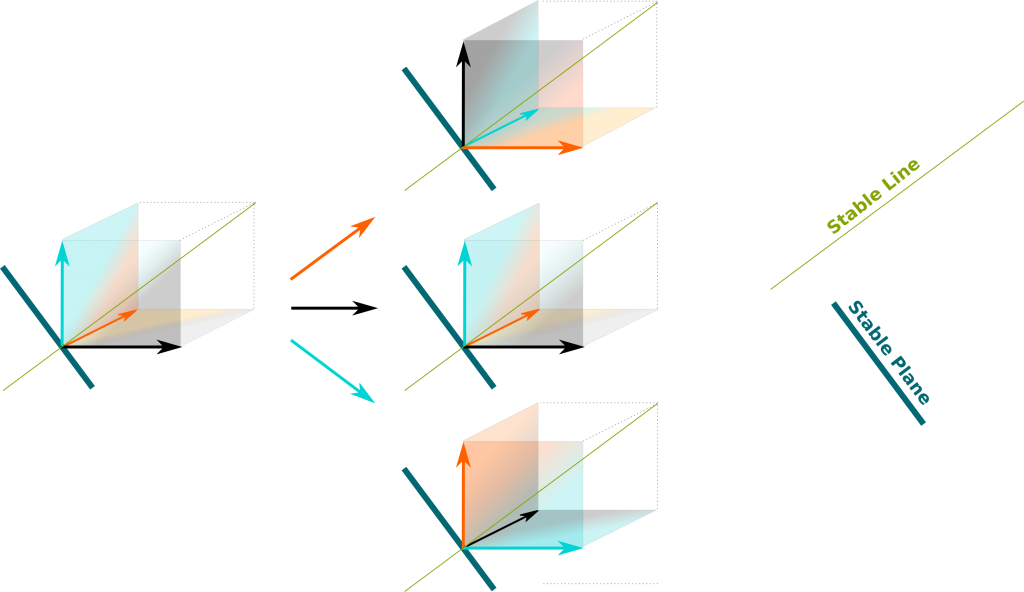

Leave a Reply