I never read original papers of the greatest scientists, but I got so intrigued by the information theory that I gave Claude Shannon’s seminal paper a read. This paper is mind-blowing! In this single paper, Shannon introduced this new fundamental theory. He raised the right questions, which no one else even thought of asking. This would have been enough to make this contribution earthshaking. But amazingly enough, Shannon also provided most of the right answers with class and elegance. In comparison, it took decades for a dozen of top physicists to define the basics of quantum theory. Meanwhile, Shannon constructed something equivalent, all by himself, in a single paper.
Shannon’s theory has since transformed the world like no other ever had, from information technologies to telecommunications, from theoretical physics to economical globalization, from everyday life to philosophy. But instead of taking my words for it, listen to Jim Al-Khalili on BBC Horizon:
I don’t think Shannon has had the credits he deserves. He should be right up there, near Darwin and Einstein, among the few greatest scientists mankind has ever had the chance to have. Yet, he’s hardly known by the public… More than an explanation of Shannon’s ideas, this article is a tribute to him.
Bits
Now, to understand how important his ideas are, let’s go back in time and consider telecommunications in the 1940s. Back then, the telephone network was quickly developing, both in North America and Europe. The two networks then got connected. But when a message was sent through the Atlantic Ocean, it couldn’t be read at the other end.
As the message travelled through the Atlantic Ocean, it got weakened and weakened. Eventually, it was so weak that it was unreadable. Imagine the message was the logo of Science4All. The following figure displays what happened:
This was what was proposed by engineers. However, this led them to face the actual problem of communication.
The unpredictable perturbation of the message! This perturbation is called noise. This noise is precisely what prevents a message from getting through.
When you’re amplifying the message, you’re also amplifying the noise. Thus, even though the noise is small, as you amplify the message over and over, the noise eventually gets bigger than the message. And if the noise is bigger than the message, then the message cannot be read. This is displayed below:
At that time, it seemed to be impossible to get rid of the noise. There really seemed to be this fundamental limit to communication over long distances. No matter when or how you amplify the message, the noise will still be much bigger than the message once it arrives in Europe. But then came Claude Shannon…
Wonders! Among these wonders was an amazingly simple solution to communication. This idea comes from the observation that all messages can be converted into binary digits, better known as bits. For instance, using the PNG format, the logo of Science4All can be digitized into bits as follows:
This digitization of messages has revolutionized our world in a way that we too often forget to be fascinated by.
Now, instead of simply amplifying the message, we can read it before. Because the digitized message is a sequel of 0s and 1s, it can be read and repeated exactly. By replacing simple amplifiers by readers and amplifiers (known as regenerative repeaters), we can now easily get messages through the Atlantic Ocean. And all over the world, as displayed below:
Now, in the first page of his article, Shannon clearly says that the idea of bits is J. W. Tukey’s. But, in a sense, this digitization is just an approximation of Shannon’s more fundamental concept of bits. This more fundamental concept of bits is the quantification of information, and is sometimes referred to as Shannon’s Bits.
Shannon’s Bits
Obviously, the most important concept of Shannon’s information theory is information. Although we all seem to have an idea of what information is, it’s nearly impossible to define it clearly. And, surely enough, the definition given by Shannon seems to come out of nowhere. But it works fantastically.
According to Shannon’s brilliant theory, the concept of information strongly depends on the context. For instance, my full first name is Lê Nguyên. But in western countries, people simply call me Lê. Meanwhile, in Vietnam, people rather use my full first name. Somehow, the word Lê is not enough to identify me in Vietnam, as it’s a common name over there. In other words, the word Lê has less information in Vietnam than in western countries. Similarly, if you talk about “the man with hair”, you are not giving away a lot of information, unless you are surrounded by soldiers who nearly all have their hair cut.
A context corresponds to what messages you expect. More precisely, the context is defined by the probability of the messages. In our example, the probability of calling someone Lê in western countries is much less likely than in Vietnam. Thus, the context of messages in Vietnam strongly differs from the context of western countries.
Well, we said that the information of Lê is greater in western countries…
Yes! If $p$ is the probability of the message, then its information is related to $1/p$. But this is not how Shannon quantified it, as this quantification would not have nice properties. Shannon’s great idea was to define information rather as the number of bits required to write the number $1/p$. This number is its logarithm in base 2, which we denote $\log_2(1/p)$.
Now, this means that it would require more bits to digitize the word Lê in western countries than in Vietnam, as displayed below:
Because of its nice properties. First, the logarithm enables to bring enormous numbers $1/p$ to more reasonable ones. But mainly, if you consider a half of a text, it is common to say that it has half the information of the text in its whole. This sentence can only be true if we quantify information as the logarithm of $1/p$. This is due to the property of logarithm to transform multiplication (which appears in probabilistic reasonings) into addition (which we actually use). Now, this logarithm doesn’t need to be in base 2, but for digitization and interpretation, it is very useful to do so.
This is an awesome remark! Indeed, if the fraction of the text you read is its abstract, then you already kind of know what the information the whole text has. Similarly, Lê Nguyên, even in Vietnam, doesn’t have twice the information that Lê has.
It does! And the reason it does is because the first fraction of the message modifies the context of the rest of the message. In other words, the conditional probability of the rest of the message is sensitive to the first fraction of the message. This updating process leads to counter-intuitive results, but it is an extremely powerful one. Find out more with my article on conditional probabilities.
The whole industry of new technologies and telecommunications! But let me first present you a more surprising application to the understanding of time perception explain in this TedED video by Matt Danzico. Now that you know about Shannon’s information theory, you should have a new insight into what the video talks about!
Yes! As Shannon put it in his seminal paper, telecommunication cannot be thought in terms of information of a particular message. Indeed, a communication device has to be able to work with any information of the context. This has led Shannon to (re)-define the fundamental concept of entropy, which talks about information of a context.
You should call it entropy, for two reasons. In the first place your uncertainty function has been used in statistical mechanics under that name, so it already has a name. In the second place, and more important, no one really knows what entropy really is, so in a debate you will always have the advantage.
Shannon’s Entropy
In 1877, Ludwig Boltzmann shook the world of physics by defining the entropy of gases, which greatly confirmed the atomic theory. He defined the entropy more or less as the logarithm of the number of microstates which correspond to a macrostate. For instance, a macrostate would say that a set of particles has a certain volume, pressure, mass and temperature. Meanwhile, a microstate defines the position and velocity of every particle.
The brilliance of Shannon was to focus on the essence of Boltzmann’s idea and to provide the broader framework in which to define entropy.
Shannon’s entropy is defined for a context and equals the average amount of information provided by messages of the context. Since each message is given with probability $p$ and has information $log_2(1/p)$, the average amount of information is the sum for all messages of $p \log_2(1/p)$. This is explained in the following figure, where each color stands for a possible message of the context:
In Boltzmann’s setting, all microstates are assumed equally likely. Thus, for all microstate, $1/p$ equals the number of microstates. The average amount of information is therefore the logarithm of the number of microstates. This shows that Boltzmann’s entropy is nothing more than Shannon’s entropy applied to equiprobable microstates.
This is another important interpretation of entropy. For the average information to be high, the context must allow for a large number of unlikely events. Another way of phrasing this is to say that there is a lot of uncertainties in the context. In other words, entropy is a measure of the spreading of a probability. This spreading is what’s often referred to as disorder. In some sense, the second law of thermodynamics which states that entropy cannot decrease can be reinterpreted as the increasing impossibility of defining precise contexts on a macroscopic level.
It is essential! The most important application probably regards data compression. Indeed, the entropy provides the theoretical limit to the average number of bits to code a message of a context. It also gives an insight into how to do so. Data compression has been applied to image, audio or file compressing, and is now essential on the Web. Youtube videos can now be compressed enough to surf all over the Internet! But before talking about communication, let’s dig in a major variant of entropy.
Shannon’s Equivocation
By considering a conditional probability, Shannon defined conditional entropy, also known as Shannon’s equivocations. Let’s consider the entropy of a message conditional to its introduction. For any given introduction, the message can be described with a conditional probability. This defines a entropy conditional to the given introduction. Now, the conditional entropy is the average of this entropy conditional to the given introduction, when this given introduction follows the probabilistic distribution of introductions. Roughly said, the conditional entropy is the average added information of the message given its introduction.
I know! But if you manage to get your head around that, you’ll understand much of the greatest ideas of Shannon.
Yes! Common sense says that the added information of a message to its introduction should not be larger than the information of the message. This translates into saying that the conditional entropy should be lower than the non-conditional entropy. This is a theorem proven by Shannon! In fact, he went further and quantified this sentence: The entropy of a message is the sum of the entropy of its introduction and the entropy of the message conditional to its introduction!
Fortunately, everything can be more easily understood on a figure. The amount of information of the introduction and the message can be drawn as circles. Because they are not independent, they have some mutual information, which is the intersection of the circles. The conditional entropies correspond to what’s missing from the mutual information to retrieve the entire entropies:
Let’see examples. On the left of the following figure is the entropies of two coins thrown independently. On the right is the case where only one coin is thrown, and where the blue corresponds to a sensor which says which face the coin fell on. The sensor has two positions (heads or tails), but, now, all the information is mutual:
As you can see, in the second case, conditional entropies are nil. Indeed, once we know the result of the sensor, then the coin no longer provides any information. Thus, in average, the conditional information of the coin is zero. In other words, the conditional entropy is nil.
It surely is! In fact, it’s so powerful that some of the weirdest phenomena of quantum mechanics like the mysterious entanglement might be explainable with a generalization of information theory known as quantum information theory.
They’re essential to understand sequences of symbols. Indeed, if you try to encode a message by encoding each character individually, you will be consuming space to repeat mutual information. In fact, as Shannon studied the English language, he noticed that the conditional entropy of a letter knowing the previous one is greatly decreased from its non-conditional entropy. Indeed, if a word starts with a r, then it’s very likely (sure?) that the next letter will be a vowel.
So to optimally compress the information of a text, it’s not enough to encode each character separately like the Morse code does. The structure of information also lies in the concatenation into longer texts. In fact, Shannon defined the entropy of each character as the limit of the entropy of messages of great size divided by the size.
As it turns out, the decrease of entropy when we consider concatenations of letters and words is a common feature of all human languages… and of dolphin languages too! This has led extraterrestrial intelligence seekers to search for electromagnetic signals from outer spaces which share this common feature too, as explained in this brilliant video by Art of the Problem:
In some sense, researchers assimilate intelligence to the mere ability to decrease entropy. What an interesting thing to ponder upon!
Shannon’s Capacity
Let’s now talk about communication! A communication consists in a sending of symbols through a channel to some other end. Now, we usually consider that this channel can carry a limited amount of information every second. Shannon calls this limit the capacity of the channel. It is measured in bits per second, although nowadays we rather use units like megabits per second (Mbit/s) or megabytes per second (MB/s).
The channel is usually using a physical measurable quantity to send a message. This can be the pressure of air in case of oral communication. For longer telecommunications, we use the electromagnetic field. The message is then encoded by mixing it into a high frequency signal. The frequency of the signal is the limit, as using messages with higher frequencies would profoundly modify the fundamental frequency of the signal. But don’t bother too much with these details. What’s of concern to us here is that a channel has a capacity.
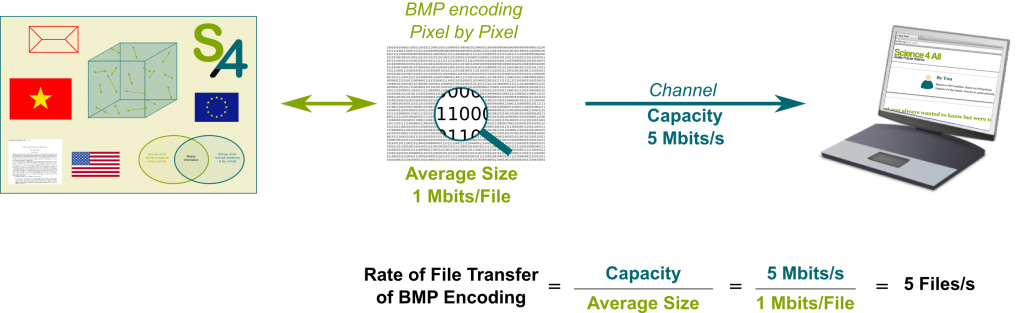
Sure. Imagine there was a gigantic network of telecommunication spread all over the world to exchange data, like texts and images. Let’s call it the Internet. How fast can we download images from the servers of the Internet to our computers? Using the basic formatting called Bitmap or BMP, we can encode images pixels per pixels. The encoded images are then decomposed into a certain number of bits. The average rate of transfer is then deduced from the average size of encoded images and the channel’s capacity:
In the example, using bitmap encoding, the images can be transfered at the rate of 5 images per second. In the webpage you are currently looking at, there are about a dozen images. This means that more than 2 seconds would be required for the webpage to be downloaded on your computer. That’s not very fast…
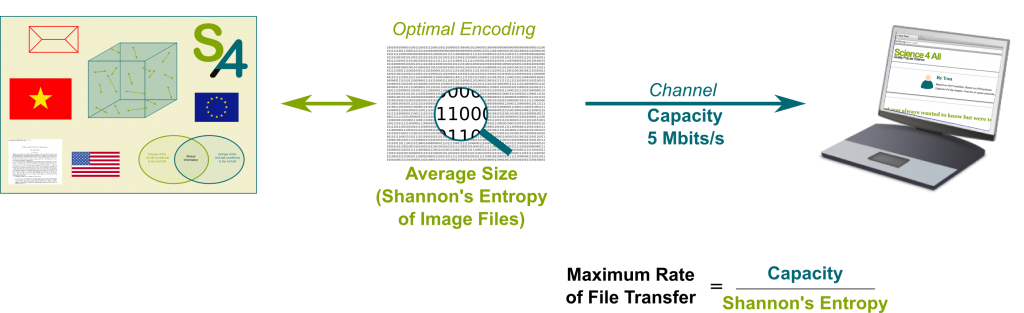
Yes, we can. The capacity cannot be exceed, but the encoding of images can be improved. Now, what Shannon proved is that we can come up with encodings such that the average size of the images nearly maps Shannon’s entropy! With these nearly optimal encodings, an optimal rate of image file transfer can be reached, as displayed below:
This formula is called Shannon’s fundamental theorem of noiseless channels. It is basically a direct application of the concept of entropy.
I mean that we have here assumed that the received data was identical to what’s sent! This is not the case in actual communication. As opposed to what we have discussed in the first section of this article, even bits can be badly communicated.
Shannon’s Redundancy
In actual communication, it’s possible that 10% of the bits get wrong.
No! The problem is that we don’t know which are the bits which got wrong. In your case, the information that gets through is thus less than 90%.
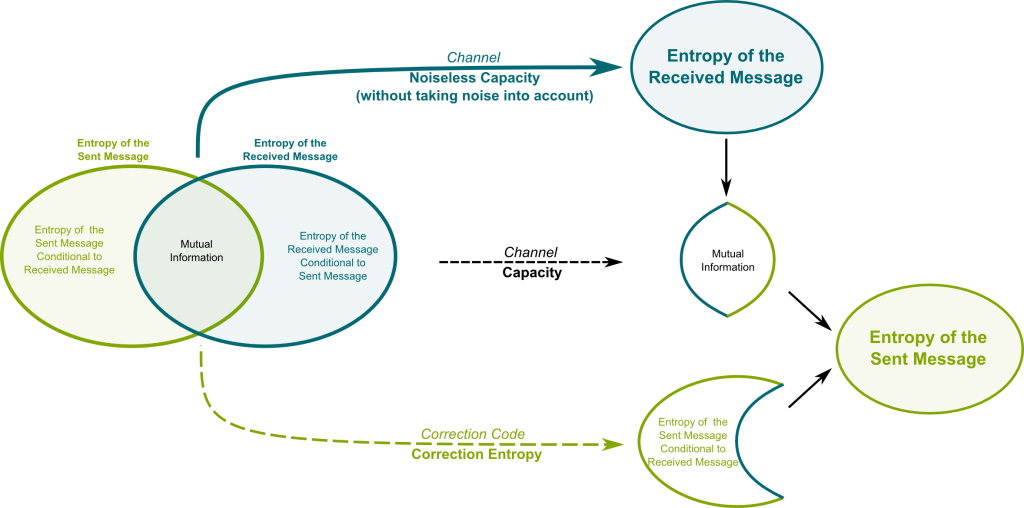
His amazing insight was to consider that the received deformed message is still described by a probability, which is conditional to the sent message. This is where the language of equivocation or conditional entropy is essential. In the noiseless case, given a sent message, the received message is certain. In other words, the conditional probability is reduced to a probability 1 that the received message is the sent message. In Shannon’s powerful language, this all beautifully boils down to saying that the conditional entropy of the received message is nil. Or, even more precisely, the mutual information equals both the entropies of the received and of the sent message. Just like the sensor detecting the coin in the above example.
The relevant information received at the other end is the mutual information. This mutual information is precisely the entropy communicated by the channel. Shannon’s revolutionary theorem says that we can provide the missing information by sending a correction message whose entropy is this conditional entropy of the sent message given the received message. This correction message is known as Shannon’s redundancy.
This fundamental theorem is described in the following figure, where the word entropy can be replaced by average information:
Shannon proved that by adding redundancy with enough entropy, we could reconstruct the information perfectly almost surely (with a probability as close to 1 as possible). This idea is another of Shannon’s earthshaking idea. Quite often, the redundant message is sent with the message, and guarantees that, almost surely, the message will be readable once received. It’s like having to read articles again and again to finally retrieve its information.
There are smarter ways to do so, as my students sometimes recall me by asking me to reexplain reasonings differently. Shannon worked on that later, and managed other remarkable breakthroughs. Similarly to theorems I have mentioned above, Shannon’s theorem for noisy channels provides a limit to the minimum quantity of redundancy required to almost surely retrieve the message. In practice, this limit is hard to reach though, as it depends on the probabilistic structure of the information.
Yes! Redundancy is essential in common languages, as we don’t actually catch most of what’s said. But, because English is so redundant, we can guess what’s missing from what we’ve heard. For instance, whenever you hear I l*v* cake, you can easily fill the blank. What’s particularly surprising is that we actually do most of this reconstitution without even being aware of it! You don’t believe me? Check the McGurk effect, explained here by Myles Power and Alex Dainis:
It wouldn’t surprise me to find out that languages are nearly optimized for oral communications in Shannon’s sense. Although there definitely are other factors coming in play, which have to explain, for instance, why the French language is so more redundant than English…
Let’s Conclude
What I’ve presented here are just the few fundamental ideas of Shannon for messages with discrete probabilities. Claude Shannon then moves on generalizing these ideas to discuss communication using actual electromagnetic signals, whose probabilities now have to be described using probabilistic density functions. Although this doesn’t affect the profound fundamental ideas of information and communication, it does lead to a much more complex mathematical study. Once again, Shannon’s work is fantastic. But, instead of trusting me, you probably should rather listen to his colleagues who have inherited his theory in this documentary by UCTV:
Shannon did not only write the 1948 paper. In fact, the first major breakthrough he did was back when he was a Master’s student at MIT. His thesis is by far the most influential Master’s thesis of all time, as it shows how exploiting boolean algebra could enable to produce machines that would compute anything. In other words, in his Master’s thesis, Shannon drew the blueprints of computers! Shannon also made crucial progress in cryptography and artificial intelligence.
I can only invite you to go further and learn more. This is what’s commonly called open your mind. I’m going to conclude with this, but in Shannon’s language… Increase the entropy of your thoughts!






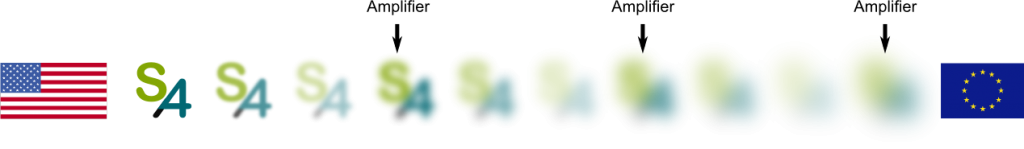

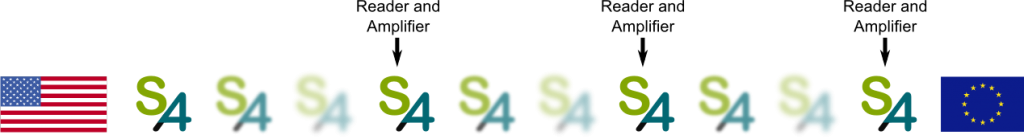




I’m confused by the claim that log (1/p) is the number if bits required to write 1/p. It seems to me rhus depends on the number of digits of 1/p. For example what if p = 1/pi – as p can be any real number between 0 and 1 it could take an infinite number of bits – there are uncountably infinite real numbers between 0 and 1
Hi Jeff! Note that p is the probability of a message, not the message itself. So, if you want to find the most efficient way to write pi, the question you should ask is not what pi is, but how often we mention it. It turns out that in maths, we do often mention pi, so we find a compact way to represent it: We call it “pi”, hence using only 2 letters (and even only one if we use Greek letters!).
The decimal representation of pi is just another not-very-convenient way to refer to pi.
Regarding other real numbers, well, almost all of them have never been studied, so their probability of being mentioned is literally p=0, which corresponds to an encryption into log(1/p)=∞ bits. This is consistent with the intuition you’re referring to!
“… Wonders! Among these wonders was an amazingly simple solution to communication. This idea comes from the observation that all messages can be converted into binary digits, better known as bits. … ”
Here you repeat yet again the false claim that the conversion of information into digital form was ‘invented’ by Claude Shannon when it had, of course, already been invented, in 1937, by English engineer Alec Reeves working in Paris for Western Electric. Why do Americans, in particular, have so little respect for Reeves (who invented digital technology in practice) and perhaps rather to much for Shannon who – belatedy – developed the relevant theory ?
Hi David! I have not read enough about Reeves to comment. All I can say is that Shannon’s explanations convinced many others that bits were the way to go. Having said that, I hope you’ll forgive my ignorance and the many oversimplifications that allow for a better story-telling. I just want to get people excited about information theory.
PS: I’m not American btw…