Entropy and the Second Law of Thermodynamics

The second law of thermodynamics is arguably the most misunderstood law of physics. And not only by students. Even the greatest physicists have trouble making sense of it! Personally, it’s the one that puzzles and fascinates me the most in physics!

On his quest to understand the illusion of time, Brian Greene takes us through some puzzling thoughts on this famous law, on NOVA’s Fabric of the Cosmos:

Cards and Entropy

Let’s start by explaining what entropy is. To do so, consider a deck of 52 cards we’ve just bought. Do you know what’s special about such a deck of cards?

Exactly! Even before looking at the cards, I can expect them to be ordered in a specific way.

As far as I know, yes. They may be arranged colors by colors or number by number, colors being ordered in any possible way, numbers being ordered increasingly or decreasingly, from the 2 or the Ace. Still, even with all these possibilities, there are only 192 arrangements we can expect from a deck of cards just bought.

Trust me! Now, information theory says that this uncertainty we have about which of these arrangements the deck of cards actually is can be associated with an entropy. This entropy is defined as the logarithm of the number of possible arrangements. Following Shannon, let’s use the base 2 logarithm. In our case, the entropy of a deck of cards we have just bought is then $S = \log_2 192 \approx 7.6$. This entropy is sort of the number of bits you need to write down the number of possible arrangements.

Entropy measures the number of possible arrangements of cards, given our knowledge that they have just been bought. Thus, it measures how much we still don’t know about the exact arrangement of cards. Once we actually look at the arrangement of cards, we learn new information about these cards. Shannon’s key insight is to discover that the amount of information we have learned equals how much we didn’t know before learning. In other words, information is the anterior uncertainty.

Exactly! If I shuffle the cards once, then it’s much harder to predict in which configuration they will be. However, my weak shuffling skills won’t totally fool you! There will still be strong patterns in the kind of configurations you’d expect to find. For instance, if you witness a sequence of 2-3-4 of spades, then you’ll be able to predict that the next card is likely to be a 5 of spades.

In such a case, the entropy will only have slightly increased…

Exactly! Eventually, all arrangements of cards will be equally likely, and we’ll have reached the state of maximal entropy. In this state, there are 52 possibilities for the first card of the deck, 51 for the second, 50 for the third… and so on! In total, there will be $52 \times 51 \times 50 \times … \times 1 = 52! \approx 10^{68} \approx 2^{226}$ possible arrangements. Hence the entropy will equal $226$. At this point, strong patterns such as 5 consecutive spades in a row will only scarcely appear. Rather, similar cards will be well spread in the deck!

Interestingly, yes. The spreading of similar cards is indeed a good indication of how much disorder there is in the cards. Because of this, we often assimilate the uncertainty about the deck of cards with the spreading of similar cards.

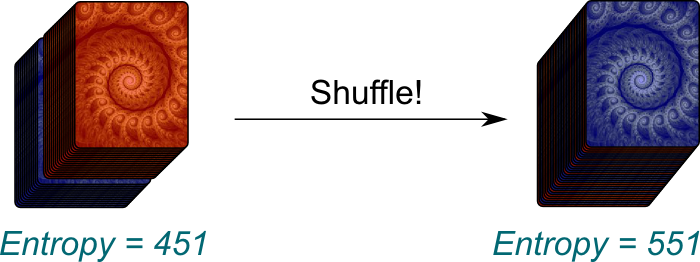
Let’s have a thought experiment to convince ourselves that they are pretty much one same thing. Consider two decks of cards, one with red backs of the cards, the other with blue ones. If we just pile up the first deck on top of the second one, even after having shuffled each deck separately, then the red cards won’t be spread in the large deck we now have. There is some order in the total deck.

Humm… There are $(52!)^2 \approx 10^{136} \approx 2^{451}$ arrangements where all the red cards are on the top. This is a lot! However, if you completely shuffle the whole deck, there will now be $104! \approx 10^{166} \approx 2^{551}$ possible arrangements! Thus, by shuffling the whole deck, we can increase the entropy by about $551-451 \approx 100$.

Not just slightly! The fact that entropy has increased by 100 means that there is a probability of only $1/2^{100} \approx 10^{-31}$ that all the red cards end up at the top of the deck. In other words, it is terribly unlikely!

It is! Huge and tiny numbers are in fact so different from the ones we usually deal with that our intuition often mislead us as we talk about them. That’s why I think that now is a good moment to pause and reflect on the hugeness and tininess of such numbers! Here’s an extract from my talk A Trek through 20th Century Mathematics on big numbers to help you in your thoughts:

In comparison, the probability of the Sun exploding on a particular second is overwhelmingly more likely than having all the red cards coming back on top of the deck!

Let’s sum up what cards have illustrated. First, the entropy is a measure of the uncertainty we have regarding a deck of cards. Second, a great indication of the entropy of the deck of cards is the spreading of similar cards, which we often assimilate with disorder.

Thermodynamics and Second Law

Now that you fully understand entropy…

Hummm… Now that you have an idea of what entropy is, let’s talk about thermodynamics!

Literally, thermodynamics is the study of the motion of heat. Its foundations were laid by French engineer Sadi Carnot, as he studied the steam machines which were giving England a major military advantage. In particular, Carnot found out that the motion of heat was more powerful when it was moving between two gases of greater temperature difference. This is what’s explained in the following extract of BBC’s great show Order and Disorder: Energy hosted by Jim Al-Khalili:

But the most amazing breakthrough of this new scientific theory is rather due to Rudolf Clausius. The German physicist made the stumbling discovery that hot objects tend to cool, while freezing objects tend to warm up!

I know it doesn’t sound like much, but it really is! Behind this remark actually lies the second law of thermodynamics! First, it yields a description of the direction in which heat moves. But more importantly, this key insight then leads directly to fundamental aspects of our universe. But before getting there, let’s understand why this law holds!

Clausius didn’t figure it out. He just took it for granted. However, the revolutionary Austrian Ludwig Boltzmann did. Boltzmann is easily one of the few greatest minds science has ever had. By daring to postulate the existence of atoms, and by working out the power of mathematics to deduce the consequences of such a postulate, he offered a fundamental understanding of heat. In particular, he went on deriving Clausius’ second law of thermodynamics from Newton’s laws and the atomic hypothesis! But more importantly, he gave an insightful definition to Clausius’ blurry concept of entropy!

In Newton’s mechanics, the entire information about gas is describable by the position and velocities of all its particles. This is known as a microstate. However, what we can measure about a gas is limited to its volume, pressure, temperature and mass. Plus, all these measures only make sense when we consider a sufficiently large pool of particles which are sufficiently similar, as their properties can then average out. For this reason, these measures are known as macroscopic information, and they define a macrostate. Following our analogy with cards, this macrostate is sort of the description of the density of red cards in each half of the total deck.

Well, if I tell you that half of the first half of the deck are red cards, then you still don’t know precisely which cards are which! There is still uncertainty, there is still a big entropy. Similarly, the entropy of a gas is the microscopic information given the context of the macroscopic information. More precisely, the entropy is the logarithm of the number of microstates corresponding to a given macrostate.

This definition corresponds to Ludwig Boltzmann’s legendary equation $S = k \log W$, where $S$ is the entropy, $W$ the number of microstates and $k$ a constant to make the concepts compatible with Clausius’ anterior definition of entropy. Arguably, this is one of the most important equation of the whole of physics. In fact, Boltzmann found it so beautiful that he had it carved on his tombstone!

Now, as I said, Boltzmann went on using his definition to prove the second law of thermodynamics!

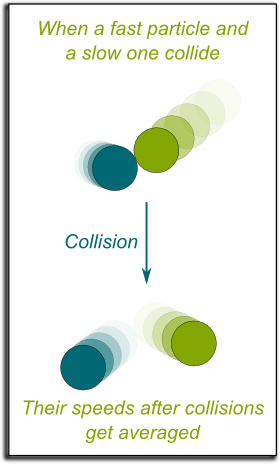
By observing that the speeds of two particles tend to be averaged when they collide, Boltzmann proved that spreading of positions and uniformization of speeds were deduced from Newton’s laws. Indeed, whenever a fast moving particle would hit a slow moving one, it would be slowed down, while the slow moving particle would get slightly accelerated. Thus, collisions after collisions, the speeds of all particles would eventually become similar, making them hardly distinguishable.

Yes! Given a macrostate, all similar particles become interchangeable. So, the more similar particles are, the more equivalent microstates there are! In other words, entropy increases. That’s what the second law of thermodynamics says!

Yes! More precisely, Clausius postulated that temperatures always tended to average out. Doesn’t that sound a lot like entropy increasing?

Formally, the law says that, in any closed system, entropy always increases. Keep in mind that this only holds for closed system. In fact, if you are allowed to act on a closed system, then it’s no longer closed and it’s quite easy to make its entropy decrease! For instance, in our example of cards, we can always use our energy to sort them out to decrease its entropy!

But the beauty of this law is its generalization way beyond the field of thermodynamics, which Clausius himself dared to undertake… This is what Jim Al-Khalili explains in the following extract:

The Arrow of Time

But this also leads us to something even more fundamental about our universe, which is the puzzling question I was referring to in the introduction, and which Brian Greene had hinted at.

It’s known as Johann Loschmidt’s paradox. As Loschmidt pointed it out, the second law of thermodynamics, as proved by Boltzmann, is not a fundamental law. It’s an emerging fact about our universe. Yet, all the fundamental laws of our universe are reversible. This means that there is a perfect symmetry between going forwards and backwards in time.

The trouble is that the second law of thermodynamics is highly irreversible! Typically, once two gases mix in a closed system, they cannot unmix. But how can the reversibility of fundamental laws disappear in emerging laws? How can it be that the reversibility of particles create the irreversibility of gases? How can forwards and backwards in time be so different at our scales, while they are fundamentally identical at the lowest scales?

If you don’t like mine, listen to Brian Greene’s:

In particular, Johann Loschmidt pointed out that if all velocities of all particles were inverted, then we would have a universe in which entropy decreases!

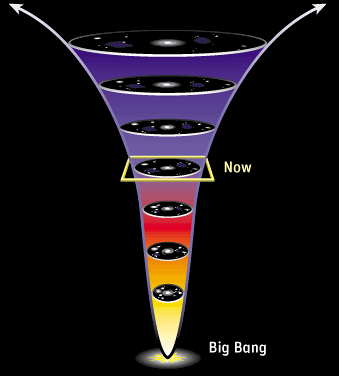
To find an answer, let’s get back to our deck of cards. If I get to increase its entropy by shuffling it, it must be because it hadn’t reached its state of maximal entropy before I shuffled! In other words, to create disorder, one has to be acting on… an ordered object! Similarly, if the second law of thermodynamics has been holding for the last 24 hours, that must be because the entropy of our universe was lower yesterday.

Exactly! So, in some sense, the source of the lowness of entropy today is due to its being even lower yesterday. But this is due to its being even lower the day before… And so on all the way towards the past…

Precisely! This reasoning proves that if the universe follows fundamentally reversible laws while having an arrow of time, that must be because it started at an extraordinarily and surprisingly low entropy state! This is what’s explained by Sean Caroll on Minute Physics:

Hehe… You’ve been reading carefully! That’s great! The fact that the entropy of the Big Bang is low despite it being nearly homogeneous is due to gravity. Now, describing the entropy of gravity is still an open question if I trust Sean Carroll’s blog. But, intuitvely, we can have an idea of the tininess of the entropy of the early universe compared to that of black holes.

What characterizes black holes is the fact that when an object falls in them, the entire information about the object is forever hidden for us. Meanwhile, according to recent results, a black hole is fully describable by merely three macroscopic information, namely, its mass, angular momentum and electric charge. Thus, the number of possible ways to make up a black hole which fits a certain macroscopic description is extremely huge. That’s why black holes have huge entropy, which is definitely much much larger than the one of our early universe in which particles had to be arranged in a very specific way so that they didn’t form a black hole! Check this video that explains that:

Sadly, yes. First, far in the future, black holes will devour everything. By doing so they will greatly increase the entropy of the universe. But this entropy will then become maximal as the black holes will vanish by Hawking’s radiation. Eventually, the universe will be a giant empty soup that solitary radiations will be crossing uniformly. This is known as heat death, as explained by Brian Greene and his colleagues:

Ironically, in times, the universe will no longer have time…

Boltzmann Brain

Still, there is one question we haven’t answered…

It’s the question of why our universe started with a low entropy state. What mechanism led to this low entropy? One easy answer consists in saying that the Big Bang was just a very special event… and to leave stuffs here. Just like a set of cards we just bought is ordered, because that’s what we get by buying it, our universe was initially ordered because that’s just how it was when it started… I don’t know about you, but I don’t find it satisfactory!

No… But I’m going to tell you Boltzmann’s, which is both worse and beautiful… Boltzmann imagined that our universe was nearly infinite, with particles flying around. This great universe, according to Boltzmann, has reached thermodynamical equilibrium and maximal entropy a long time ago. However, after extremely long periods of times, just for statistical reasons, some structures will appear. These fluctuations can then be a source of order to create a universe.

Not according to Sir Arthur Eddington, as he pointed out himself that there was a huge problem with this story.

For the universe to be interesting, Boltzmann considered that it had to be inhabitable by an intelligent being. This intelligent being is known as a Boltzmann brain. Boltzmann then considered that we were more likely to be the kind of Boltzmann brains which are the most frequent in his everlasting nearly infinite universe.

Yes… But, amusingly, it doesn’t take the creation of the whole universe to create a Boltzmann brain! In fact, the kind of fluctuations it requires to have a Boltzmann brain only is much smaller than the kind of fluctuations which would create a universe like ours! After all, our universe is gigantic compared to the Boltzmann brains it inhabits. And here comes the catch…

A universe with a Boltzmann brain only is overwhelmingly more likely than our particular universe! In other words, in Boltzmann’s infinite universe, there will be many more isolated Boltzmann brains in not-that-low entropy regions than Boltzmann brains in actual very low entropy in a universe like ours! Following Boltzmann’s arguments… we should be isolated Boltzmann brains in a small region of the universe with nearly maximal entropy!

I know!

That’s the most puzzling fact about the second law of thermodynamics, and it’s an open problem!

I think we’ve come to the point where I feel more comfortable letting an expert talk. Here’s a great presentation by Sean Carroll:

Let’s Conclude

What I like about the second law of thermodynamics is that it really is a mathematical riddle. How can irreversibility emerge from reversibility? How can macroscopic information always go into microscopic information? It’s a shame that the increase of entropy is hardly ever connected to these questions, which, from a fundamental perspective, are particularly breathtaking. And it’s quite a remarkable fact that the answer lies in the inaccessible secrets of the Big Bang. Well, inaccessible so far…

Finally, note that mathematically speaking, not much is fully understood regarding entropy of gases. For instance, it was only in 1973 that Lanford proved that Boltzmann’s equations actually held in a simple case for a certain time. This doesn’t sound like much, but it’s more or less the best we have proved! Like in the Navier-Stokes equation problem, the difficulty comes from the lack of regularity of functions which arise from their confinement in space for instance. This prevents mathematicians from using classical partial differential equations. Recently, a lot of progress has been made by French 2010 Fields medalist Cédric Villani, as he managed to address rigorously the question of the speed of increase of entropy. Surprisingly, this speed is not constant. Rather, it comes with ripples. Watch his talk to go further!