Today, theoretical physics seems in a dead-end, as its two major theories, relativity and quantum theories, appear incompatible. This would sound extremely troubling, but History tells us we have faced this problem in the past. In the early 20th century, Isaac Newton’s mechanics and James Maxwell’s electromagnetism also appear incompatible. One of them had to be false. Yet, the differences of prediction couldn’t be observed, because, they occurred for motions at very high speed, close to light speed. And just like Dr. Sheldon Cooper, scientists couldn’t go reach such speeds.
At that time, Newton’s mechanics was science’s holy grail. It took a great man, Albert Einstein, to dare to question it. In particular, he was bold enough to postulate that what numerous experiments kept proving (in particular the Michelson-Morley experiment) was true…
Wait to hear what his postulate was…
Postulates
He claimed that the speed of light was the same in any inertial system!!!
A system is an observer’s viewpoint on the universe. Now, it will be called inertial if, whenever you leave some object still in this referential and if nothing interacts with it, it will remain still. Imagine a train. Leave a luggage in it. If the train keeps turning, accelerating and breaking, the luggage will be moving accordingly for any observer of the train. But if the train is moving straight without accelerating nor breaking, then the luggage will remain still for any observer of the train. You can then pour coffee or play chess, just as if you were at home. Such straight-moving never-accelerating-nor-breaking train is thus an inertial system.
Well. Yes, you’re right. Gravity acts, and so does the floor. To imagine a real inertial referential you’d have to imagine motions in empty space where there are no interactions, not even gravity.
Now, the great properties of inertial systems is that any inertial system is in uniform translation motion with regards to any other inertial system, that is, the speed of the former is constant from the perspective of the latter. So, if Leonard is in an inertial system, then Sheldon will be still in an inertial system if and only if, from Leonard’s perpective, Sheldon’s motion is rectilinear. Assuming Leonard being in an inertial system, the following figure displays other inertial systems:
Crazy is probably everyone’s first reaction to the postulate!
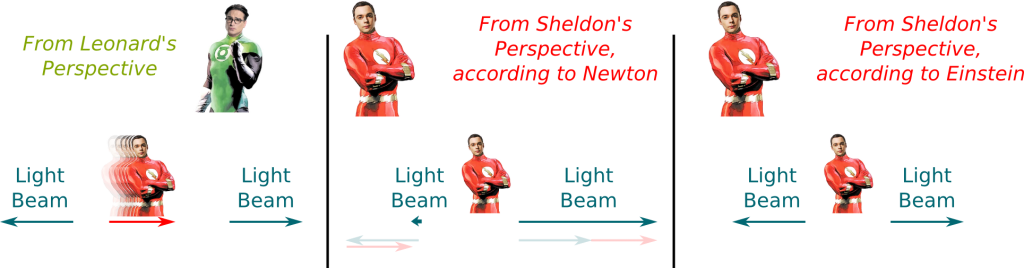
What you’re proposing to do is a thought experiment, that is, an experiment that cannot be done in practice, but on which we could still reason and apply theory. In order to consider this thought experiment, let’s assume one, say Sheldon, can go at nearly light speed:
Now, what you’re proposing corresponds to the following figure, right?
Yes, according to Newton’s mechanics. But Einstein was questioning it. He thought: What if the additivity of speed wasn’t true? By postulating the invariance of the speed of light, he envisioned another answer. But to go further, he needed two more hypotheses regarding the symmetries of space and time.
First, the relativity principle, similar to Galileo’s and Newton’s one, states that the laws of physics must be the same for every inertial system.
Second is the isotropy and homogeneity of space and time. This means that all directions of space (up-down, left-right, back-front) and all locations of space are totally symmetrical. This last postulate isn’t clearly stated as such in Einstein’s seminal paper (and in many articles on special relativity), but it’s a fundamental postulate for the theory.
All of Einstein’s special relativity theory is based on these three extremely simple principles of physics: Invariance of light speed, relativity principle and isotropy and homogeneity of space and time. These are simple laws of symmetries! From that, he constructed one of mankind’s greatest invention! How beautiful is that?
There is no paradox according to Einstein if you consider that light beam is invariant. It simply gives us the following figure:
In this figure, the longer the arrow, the faster the beam. In Newton’s theory, Sheldon observes that the beams speed are reduced or increased depending on their motions compared to his. But, counter-intuitively, not in Einstein’s theory.
No. Einstein’s ideas correspond to redefining the very nature of space and time. Compositions of any speeds can no longer be done as they used to.
Shortly said, yes. But it requires to question fundamental intuitive concepts which we took for granted. That’s what we’ll unveil in this article!
Fortunately, at that time, the mathematical tools to study the geometry Einstein was defining already existed, thanks to previous works by George FitzGerald, Joseph Larmor, Hendrik Lorentz and Henri Poincaré. These great scientists suggested some of Einstein’s ideas, but Einstein was the one who managed to sum them all up in three astonishingly simple postulates. The theory quickly gained great success, thanks to Max Planck’s efforts of communicating it.
Let’s see what these mathematics tell us.
Simultaneity
Let’s start with the absence of simultaneity.
In fact, we can. What I meant was the absence of absolute simultaneity.
More precisely, simultaneity of events at different locations is relative. To see this, let’s consider the following thought experiment. Suppose Sheldon is carrying a double sabre laser horizontally, as he runs at speed close to light speed. Assume he turns it on. Two beams are flashed, one to the front and the other to the back.
As you can see on the figure, according to Sheldon, the two beams will reach the extremities simultaneously. But this is not the case for Leonard, for whom the first beam touches the rear before the second beam touches the front. Simultaneity is thus relative.
Chronology
No! Imagine you were moving much faster than Sheldon from left to right, that is, if Sheldon is going at 99% of light speed, you’re moving at 99.99% of light speed. Then Sheldon will appear to be moving very fast from right to left. A similar reasoning will imply that the second beam actually touches the front before the first beam touches the rear. Not only simultaneity, but also chronology are now relative to the observer!
In fact, chronology still exists for plenty of events! That’s reassuring, since otherwise, causality would be greatly questioned! In fact two events can be ordered absolutely if one is inside the light cone of the other.
The concept of light cone is important in special relativity. Its study shows the relevancy of considering space and time as a unique entity, called… spacetime! In this formalism, every event is defined by its location in spacetime, with regard to some observer.
Consider an event and assume there is a particle at that event, that is, at the location in spacetime defined by the event. The light cone of this event is the set of other events where this particle can be in the future or in the past, provided that this particle cannot travel faster than light.
To visualize it, imagine being 1 year after Sheldon’s birth in Texas. Then you’d be in the light cone if the distance between your location and Texas can be done by light in less than a year. Equivalently, you’d be in the light cone if and only if you are in less than a light-year away from Texas! The light cone at that time is therefore the inside of a sphere centered on Texas and whose radius equals a light-year Light-year is a measure of distance. It’s the distance traveled by light in a year.
Imagine space only had two dimensions. Then the light cone at any time would be a circle, with a radius equal to the time multiplied by the speed of light. If now you put time on another axis, then you can draw the light cones for every time, noticing that the radius will increase proportionally to time. This is what you’d obtain:
In this setting, chronology between the event at the center of the figure and any other events can be defined if and only if the other event is inside the light cone. For any other event, there are observers for whom the other event precedes the former and other observers for whom the other event succeeds the former. Chronology cannot be defined for them.
Dilation of Time
Let’s now go further in the study of properties of special relativity. Another thought experiment will enable us to unveil a mystery of time.
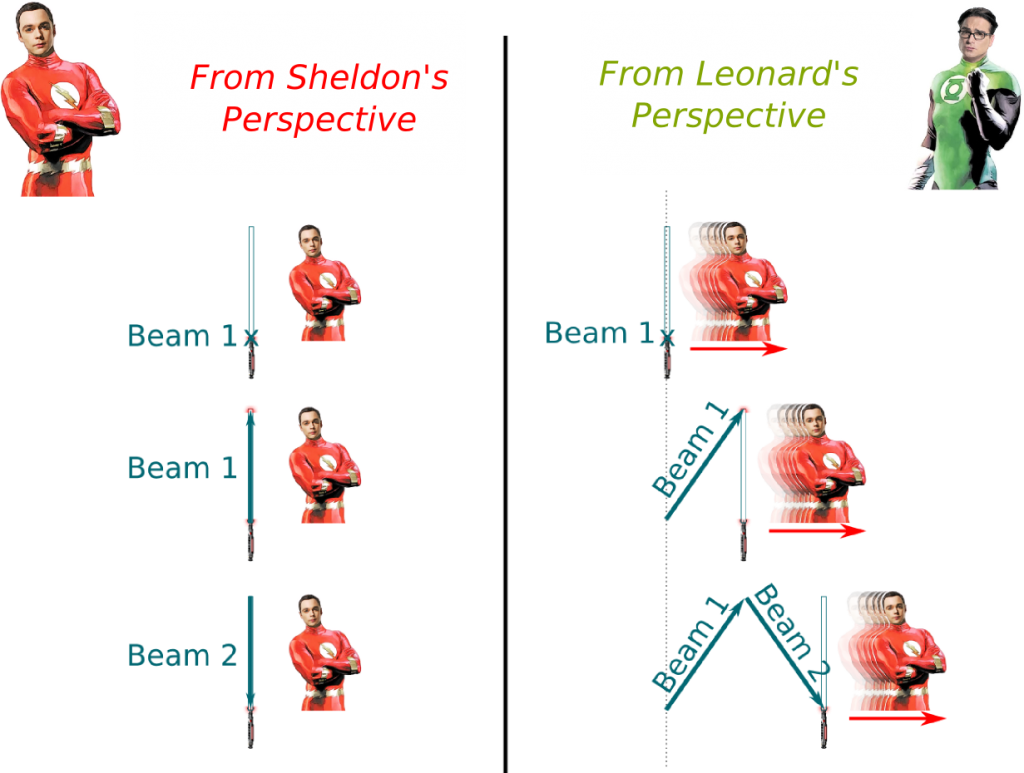
Indeed there is. To show it, let’s now imagine that Sheldon was holding a vertical sabre laser, and he turned it on as he was running. As he turns it on, a first beam goes to the top end and a second beam then comes back:
There are two important events in this thought experiment: Initially, the light beam goes from the bottom. Eventually, it reaches back the bottom. Now the time that has passed during these two events should be directly linked with the distance traveled by light, as light always travel at the same speed. Yet, according to Sheldon, you’ll see light simply going up then down. On the opposite, according to Leonard, you’d notice that light will have gone up-right then down-right. Overall, the distance traveled by light is longer from the perspective of Leonard. To travel this longer distance, light has needed more time.
This is how we come to the astonishing conclusion that time depends on the observer. Time for Leonard is longer than for Sheldon. Time is dilated! And a little bit of geometric calculations would yield the dilation factor, but for simplicity I won’t do it here…
Let me help you! In this thought experiment, Sheldon is strongly related to the events between which the time difference is measured: It’s the only inertial systems where both events occur at the same location! In the opposite, for Leonard, the locations of the two events vary.
Sure. Let’s sort it out clearly. The time between two events is not absolute. It is relative. If the two events are chronologically not comparable, then this time can take any value, positive or negative. But if the two events are chronologically comparable, there exists a unique inertial system where they occur at the same spatial location. Now, for this particular inertial system, what time dilation says is that the time between the two events is smaller than if measured in any other inertial system. Is that clearer?
Indeed it is. Imagine two twins were born at the same location and time. (I can say that they were born simultaneously, because it’s at the same location!). Call them Leonard Hofstadter and Sheldon Cooper. Leonard stays on Earth, while Sheldon embarks on a space ship, goes three times around the Milky Way and comes back to Earth. At this moment, Leonard and Sheldon meet again. The paradox is that the birth and this meeting occur at the same location in both twins’ system, implying that both Leonard and Sheldon consider that the time in his system should be smaller than the time in the other’s system. Thus, both think they are younger than the other.
Leonard and Sheldon cannot both be in an inertial system! Otherwise, they would be flying away from each other forever and never meet again!
Now, an approximation of the problem will give us a hint at the answer to who’s the youngest. Let’s consider that Sheldon goes straight to some other distant planet to visit its Grand Canyon (let’s call the other planet the Grand Canyon Planet) and comes back straight to Earth, and let’s neglect all phenomena of variations of speed which require general relativity theory. We now have an intermediate event corresponding to Sheldon reaching the Grand Canyon Planet. Yet, Sheldon is the only one for whom the three events occur at the same location. Thus, for Sheldon, time should be smaller between the first and second event, and then between the second and third event.
This gives an indication that Sheldon, the traveling brother, should actually be younger once he comes back to Earth.
Contraction of Space
Since we have considered that space and time were a single entity, and since we showed that time wasn’t absolute…
Indeed! Let’s show it!
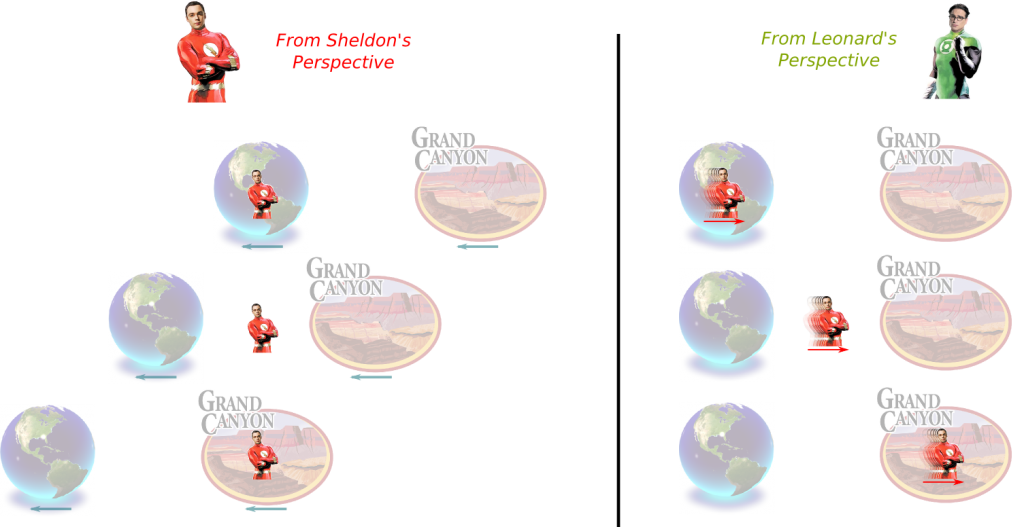
Yes. And this one is a simple one. Simply imagine Sheldon going to the Grand Canyon Planet.
Once again there are two events we’ll compare: Sheldon leaving Earth, and Sheldon arriving to the Grand Canyon Planet.
I haven’t made that point yet! Notice that, according to Sheldon, the two events occur at the same location. Thus, the time between the two events is minimal in his inertial system.
Now, the speed of the Earth and of the Grand Canyon Planet from Sheldon’s perspective is the same as the speed of Sheldon from Leonard’s perspective, who remained on Earth. Yet, the distance between the Earth and the Grand Canyon Planet is the product of this speed and the time between Sheldon’s departure and arrival. Since this time is shorter for Sheldon…/p>
There you go! As Sheldon goes at high speed, the distances he travels are reduced! Space is contracted!
Almost! The faster Sheldon is the more contracted is the space! If his speed is close to light speed then the distance will be close to 0. This indeed mean that in theory, we could travel extremely far very quickly (although, for the planets we’re travelling from and to, time would be greatly dilated, hence, when we come back to Earth, everyone we knew would have died…).
Yes there is. For Leonard this distance is maximal. But that’s not the only one for which the distance is maximal. In fact, this distance will be maximal for all inertial systems in a uniform translation motion perpendicular to the Earth-Moon axis. For instance, it’d be the case for Howard Wollowitz, if he’s traveling vertically in Leonard’s system, while the Earth-Moon axis is horizontal:
Yes, but in the direction of the motion only! The following figure shows how space is contracted, given the direction of your motion:

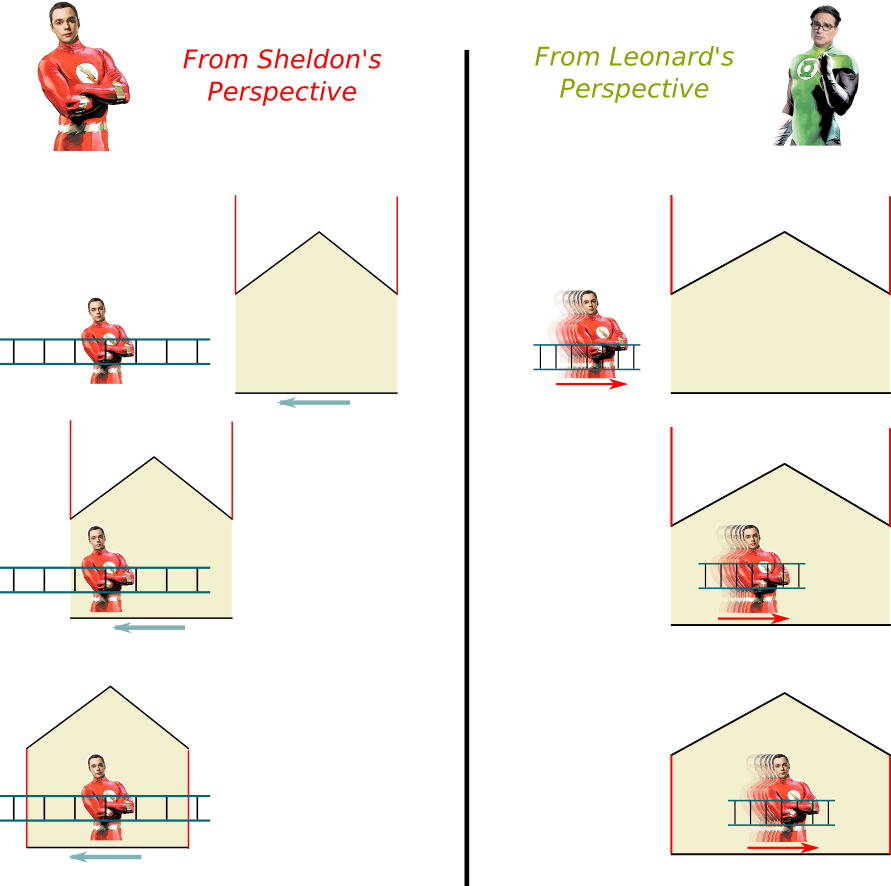
Talking about puzzles… Let’s finish by studying the ladder paradox. In this famous thought experiment, Sheldon is carrying a ladder. Leonard wants to trap him, so he builds a house whose length is equal to the length of the ladder in an inertial system where both are still. As soon as the back end of the ladder comes into the trap, the two doors of the trap close simultaneously:
Now here’s the paradox. As Sheldon runs fast, according to him, the length of the trap is contracted and is thus to small to trap him. However, according to Leonard, it’s the ladder that gets contracted, in which case, there would be no problem to trap Sheldon…
I’m the one who should be asking you! If you have carefully followed everything, you should notice what’s wrong with the reasoning…
???
Good point! You’re getting closer!
There you go!
Now, let’s assume that the doors close simultaneously for Leonard. Either Sheldon doesn’t stop and crashes into the back door or he decides to stop and gets trapped. If he doesn’t stop, in his system, he’d be seing the back door closing before him and would crash into it, before the ladder totally gets into the trap. And in the opposite case, if he stops, then in his system, it means that the trap would no longer be contracted… Once he stops, the length of the trap is just long enough for the ladder to fit. At that moment only does the front door close.
Let’s conclude
What an amazing theory, don’t you think? It’s so hard for us to imagine that such a counter-intuitive theory can better describe reality. That’s largely due to the fact that we are trapped in the partial reality given by our daily lives. Our understanding of the world is based on these daily lives, but there is no reason to believe that at different scales and different places, the world behaves according to that understanding. As relativity shows it, physics at both much higher scales is deeply counter-intuitive. And it’s so much worse at lower scales, where physics is described by quantum mechanics! By approaching these theories with our intuitive common sense, we often run into paradoxes. But these paradoxes are due to the application of our common sense, which is erroneous.
One amazing consequence of special relativity if we combine it with the big bang theory (the real one!), is the absence of a center of the universe. More precisely, any matter can be considered as the center of the universe! To visualize it, let’s assume the universe is 2-dimensional, and that Sheldon, Leonard and Howard were here at its beginning. They are all moving away from each other. From everyone’s perspective, the two others are moving away at almost light speed, just like any matter around him. After 13.75 billion years, each is thus at the center of the 13.75-billion-light-year-circle universe in his system. This shows can both Ptolemy and Copernicus were right: Both Earth and the sun are centers of the universe!
Learning these theories requires and implies the questioning of many prejudices we have. And I believe that doubting prejudices can lead to much more tolerance between apparently contradictory ideologies and religions. That’s why I would strongly recommend their teaching, even if it’s only at a basic level like the one I’m presenting here. No need of the actual technical mathematics to have a glance at why the world is not how most of us believe it is. Following this idea, I believe model-dependent realism can bring a lot to societies. Imagine Leonard and Sheldon debating about their observations of the thought experiments. Could they not realize the relativity of their observations, they would be fighting forever.
On a more technical level, let me recapitulate the mathematical magic behind Einstein’s theory. Basically, assuming the relativity principle and the isotropy and homogeneity of space and time is not enough to define its geometry. In particular, with these hypotheses only, the switching from an inertial system to another is poorly defined. One more hypothesis of invariance is required. In Newton’s theory, this invariance is the invariance of time and space. As it turned out, it was false. Einstein’s genius idea was to question this invariance and replace it by the invariance of light speed, which implied in turn the relativity of time, space, and linked ideas such as simultaneity.
That’s a great question! First, mathematically, spacetime is now the right mathematical object to study, and the tools to do so have been designed by Hermann Minkowski, which are better understood through the deeper concept of group representations. In this setting, adapting laws of Newton leads inevitably to the equivalence of mass and energy, which is captured in the famous formula E=MC2. Maxwell’s laws can now be formalized in this setting, and phenomena like the Doppler effect can be explained. However, to go even further, the tremendous giant leap Einstein made was to include gravity, by postulating the equivalence of gravity and acceleration as the bending of spacetime. You’d need to learn about Riemannian manifolds to get there… My knowledge of more advanced relativity theory is limited. If you can, please write articles to go further in reading Einstein’s mind!
The predictions of Einstein’s theory have been proven experimentally many times (GPS system, light deviation, nuclear reactions) with a remarkable accuracy. Lately though, in 2011, an experiment seemed to have questioned the whole theory, with the observation of particles faster than light, called neutrinos, by the OPERA experiment. It took scientists month to find out that a fiber optic cable was in fact poorly attached, thus creating the unexpected result. In fact, until now, Einstein’s theory match observations where it should be applied. So far so good. Yet, the theory cannot be applied for interactions of particles. Thus, there is no doubt that Einstein’s theory is at least incomplete.
To answer this question, let’s notice the hidden postulates of special relativity, which are hardly ever stated. First, it assumes the existence of an inertial system. But that’s something that general relativity will fix, as you can learn by reading Scott’s article. Second, it supposes that the transformation of coordinates when switching from an inertial system to another is linear. Third, spacetime is considered to be a 4-dimensional vectorial space, including one dimension of space. All these hidden postulates appear so obvious that they aren’t questioned. But one of them could be false… In fact, modern theories talk about adding dimensions of space (see Thibault’s article on the forces of Nature). I have probably missed other hidden hypotheses of special relativity… Please comment and help me improve the article.







Leave a Reply