Let’s start with the following calculation: $-2 = (-8)^{1/3} = (-8)^{2/6} = ((-8)^2)^{1/6} = 64^{1/6} = 2$.
The brutal answer would be that you should never write $a^p$ when $a$ is negative… But, this would conceal some wonderful underlying mathematics, including and especially the weirdness and awesomeness of imaginary and complex numbers! Let’s discover these mathematical objects in this article! Our approach will be highly geometric and, I think, much more insightful than the one you have learned (or will learn) at school.
The Geometry of $n$-th Root
To understand what just happened, let’s focus on the first equality, namely $-2 = \sqrt[3]{-8}$. It reads “$-2$ is the cube root of $-8$”. But what does that mean?
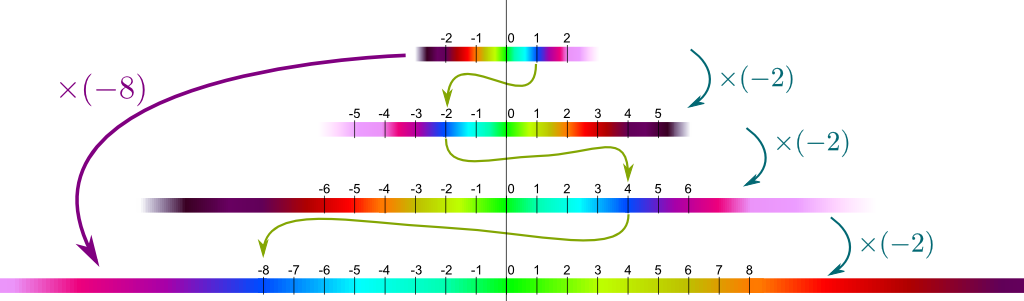
Yes! But, let’s have a geometrical understanding of what you’ve just said! To do so, notice that if we multiply both sides of the equality by any number, then the equality still holds. Indeed, if we multiply by $1$ both sides we obtain $1 \times (-2)^3 = 1 \times (-8)$, and if we multiply by $241$, we have $241 \times (-2)^3 = 241 \times (-8)$. More generally, if $x$ represents any number, we have $x \times (-2)^3 = x \times (-2) \times (-2) \times (-2) = x \times (-8)$. Thus, we can now see the operation “$\times (-2)$” as an operation on numbers, which, when applied three times, is equivalent to the operation “$\times (-8)$”!
Here’s the awesome part. These operations correspond to geometrical transformations made to the number line (they’re symmetries)! For instance, multiplying by $(-2)$ corresponds to inverting it, and stretching it by a factor 2. This is what’s done below three times!
Be patient! Let’s simplify the problem a little bit and consider the equality $-1 = (-1)^{1/3}$. What does it mean geometrically?
Yes! Now, this means that we can translate the algebraic relation $-1=(-1)^{1/3}$ by the geometrical phrase: Inverting the number line three times is equivalent to inverting it once. Sweet, isn’t it?
Hehe! The key idea of complex numbers lies in the next question… Is $(-1)$ the only one cube root of $(-1)$?
Don’t think numerically! The whole point of my construction was to consider the problem geometrically!
In other words, is there a geometrical operation on the number line, which, when applied three times, corresponds to inverting it?
Come on! You can find it!
Bingo!
In fact, there are two such 6th-of-a-turn operations, depending on whether the turn is clockwise or anti-clockwise. Below are described these two operations, each applied three times to the number line.
In addition to the “$\times (-1)$” operation, this gives us a total of three cube roots of $(-1)$!
Great questions! In fact, you should try to answer by yourself!
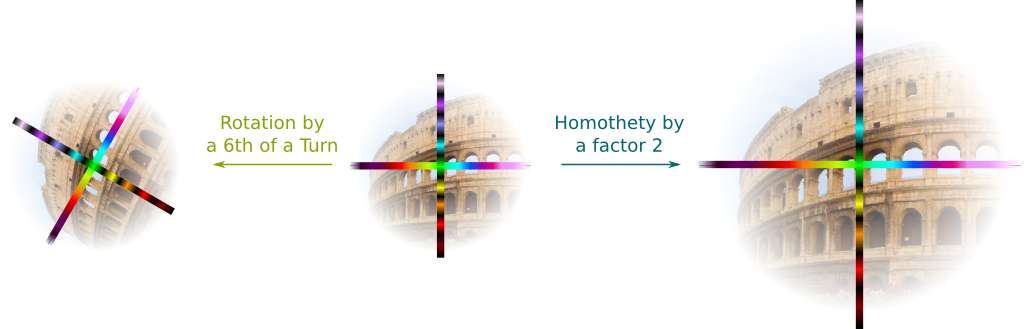
Exactly! Similarly, 6th roots of $64$ include dilations by a factor 2 combined with a rotation of one or two 6th of turn, clockwise or anti-clockwise. Plus, there are also operations “$\times (-2)$” and “$\times 2$”. This gives us six 6th roots of $64$. And as you can guess (or prove!), more generally, any number has $n$ $n$-th roots!
Once again, you should be the one who gives me the answer!
In other words, is there a geometrical transformation which, when applied twice to the number line, is equivalent to simply inverting it?
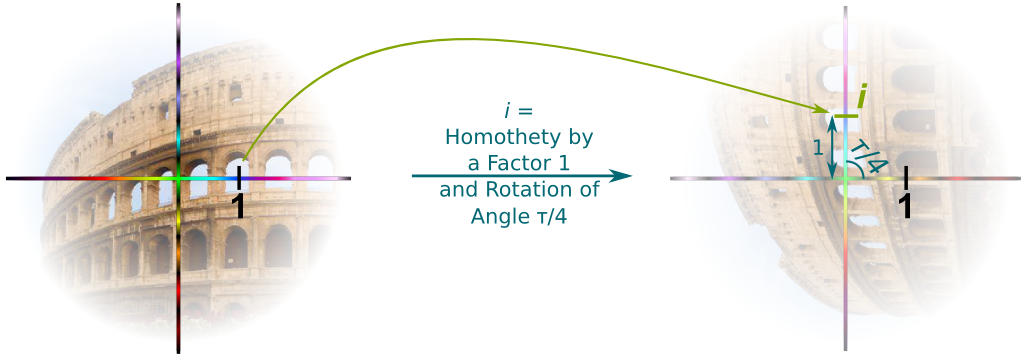
There you go! By convention, we refer to the anti-clockwise quarter-of-a-turn rotation as $i$. This $i$ is so important that we have given it different names… which I all dislike! It’s known as the imaginary number (imaginary? number?), the square root of $(-1)$, or, worst of all, $\sqrt{-1}$.
What’s very wrong is that $i$ is not the only square root of $(-1)$. The clockwise quarter-of-a-turn rotation is a square root of $(-1)$ too! Plus, if you can’t write $\sqrt[3]{-8}$, then you definitely can’t write $\sqrt{-1}$!
Hehe… We can now answer that elegantly!
Solution to the Paradox
The major flaw lies in the non-unicity of the $n$-th roots. This is what 19th-century French mathematician Évariste Galois called the ambiguity of $n$-th roots. More precisely, there’s not an actual unicity of the cube root of $(-8)$, nor is there a unicity of the 6th root of $64$. In particular, $(-2)$ is a 6th root of $64$, but it’s just not the one we refer to by $\sqrt[6]{64}$.
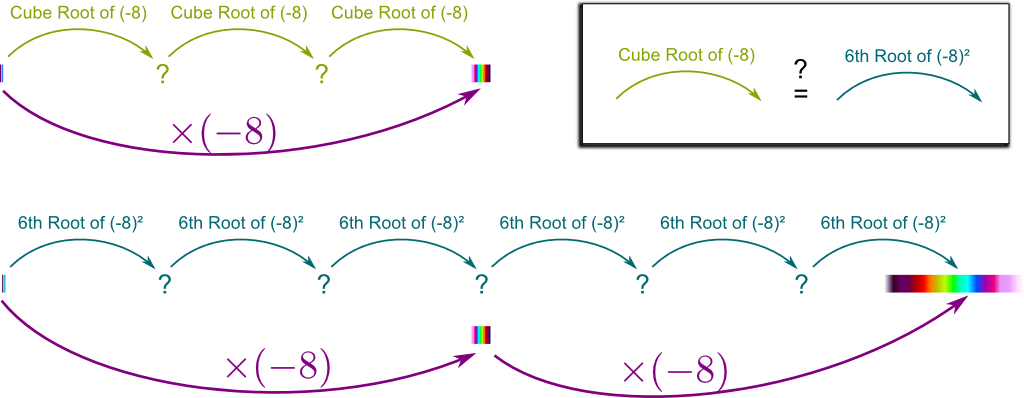
Yes. And the other flaw of the formula of the introduction lies in the relation $(-8)^{1/3} = ((-8)^2)^{1/6}$. Literally, it says that a cube root of $(-8)$ is a sixth root of the square of $(-8)$.
Once again, our salvation will come from geometry! Geometrically, this says that an operation which is equivalent to $\times (-8)$ when applied three times is equal to an operation which, when applied six times, is equivalent to applying $\times (-8)$ twice. Below is a figure which illustrates this statement.
As you can deduce it from the figure above, any cube root of $(-8)$ is also a 6th root of $64$. Indeed, applying the green operation six times will necessary be equivalent to applying “$\times (-8)$” twice. But some of the 6th roots of $64$ aren’t cube roots of $(-8)$! It’s not too hard to prove that these are the cube roots of $8$, the other square root of $64$. I invite to do that as an exercise!
Now, by denoting $\sqrt[3]{-8}$ the set of all cube roots of $-8$ and $\sqrt[6]{64}$ the set of all 6th roots of $64$, we can elegantly correct the paradox! These notations are highly non-conventional and I have been blamed for using them. But I believe it to provide an insightful and beautiful solution to the paradox. Also, if you can make the difference between $n$-th roots and the classical notation $\sqrt[n]{x}$ for $x \geq 0$, then you’ll have made a huge breakthrough in the understanding of $n$-th roots.
Homotheties and Rotations
Although insightful, the descriptions of complex numbers we have given so far aren’t very rigorous.
From a geometrical perspective, complex numbers should actually regarded as a certain collection of transformations of a plane rather than those of a line. This plane is called the complex plane. It is infinite in all directions and has a unique center, called the origin. Plus, one of its axis which goes through the origin is known as the real number line. The axis perpendicular to the real number line is known as the imaginary number line.
The transformations which corresponds to a complex numbers are those we have been using so far: homotheties and rotations centered on the origin. These two operations are the symmetries described below:
The key aspect of these operations is that any number of rotations and homotheties can be combined, and that the order in which they are combined does not matter. In technical terms we say that all these geometrical transformations are associative and commutative. Another important fact is that all usual numbers can be matched uniquely with one such geometrical operation. For instance, what’s the operation corresponding to the number $2$?
Yes, which is also known as “$\times 2$”! What about the number $(-1)$?
Nope… Keep in mind that we can only use homotheties and rotations!
Excellent! Let me give you one last example: $(-2)$ is a homothety of a factor 2 combined with a rotation of a half turn. Now, more generally, any combination of a homothety and a rotation forms a complex numbers.
Yes! Now, the homothety is defined by a positive factor called module and is commonly denoted $\rho$. By convention, the rotation is defined by an angle of anti-clockwise turn called argument and is often denoted $\theta$. Since these two parameters uniquely define the combination of a homothety and a rotation, each complex number can be represented by the couple $(\rho, \theta)$.
Well, as we’ve said, any positive number is just a homothety. This includes a rotation of angle $0$. Thus, any positive number $x$ is the complex number $(x, 0)$. Now, if $x$ is a positive number, then $(-x)$ corresponds to a homothety of factor $x$, and of a half turn. Since a half turn corresponds to angle $\pi$, the number $(-x)$ is thus the complex number $(x, \pi)$.
I know! Some mathematicians even think that $\pi$ should be withdrawn from all equations to be replaced by $\pi = \tau/2$. There’s even a manifest supporting that… as you can see it in the following awesome video by ViHart:
Humm… Good remark. We need a new transformation which corresponds to zero! This transformation consists in collapsing the whole complex plane onto its origin.
Not in an obvious one for sure! But, for one thing, we can multiply complex numbers. This corresponds to performing successively the geometric operations associated to the complex numbers. And what’s beautiful is that this has an algebraic translation! What I mean by that is that multiplying $(\rho_1, \theta_1)$ by $(\rho_2, \theta_2)$ corresponds to two homotheties by factors $\rho_1$ and $\rho_2$ and two rotations of angles $\theta_1$ and $\theta_2$. Now, two homotheties of factors $\rho_1$ and $\rho_2$ combine into a homothety of factor $\rho_1 \times \rho_2$, while two rotations of angles $\theta_1$ and $\theta_2$ result in a rotation of angle $\theta_1+\theta_2$. Thus, we have the product $(\rho_1, \theta_1) \times (\rho_2, \theta_2) = (\rho_1 \times \rho_2, \theta_1 + \theta_2)$. How sweet is that?
For reasons I won’t be dwelling on here, Leonhard Euler showed that it made sense to write the complex number $(\rho, \theta)$ as $\rho e^{i\theta}$. Given this writing, the multiplication of two complex numbers follows the usual laws of algebra, as $(\rho_1 e^{i\theta_1}) \times (\rho_2 e^{i\theta_2}) = (\rho_1 \rho_2) e^{i(\theta_1+\theta_2)}$. Also, plugging in $\rho=1$ and $\theta=\pi$, we obtain the equality $e^{i\pi} = (1, \pi) = -1$, which is usually rewritten as $e^{i\pi} + 1=0$. This beautiful formula is known as Euler’s identity! But, in spite of probably angering the Swiss scholar, I’d rather have it written with $\tau$ as $e^{i\tau} = 1$. This last formula is much more insightful, as it says that $\tau$ represents a full turn.
The ability complex numbers have to describe rotations is the reason why they are so much used in oscillating problems in physics and engineering. Instead of involving ugly trigonometry, the function $f(t)=e^{it}$ provides an elegant description of these motions, which greatly facilitates computations! But that’s still just the tip of the iceberg. To unveil the true magic of complex numbers, we’ll need to dig deeper!
Points in the Complex Plane
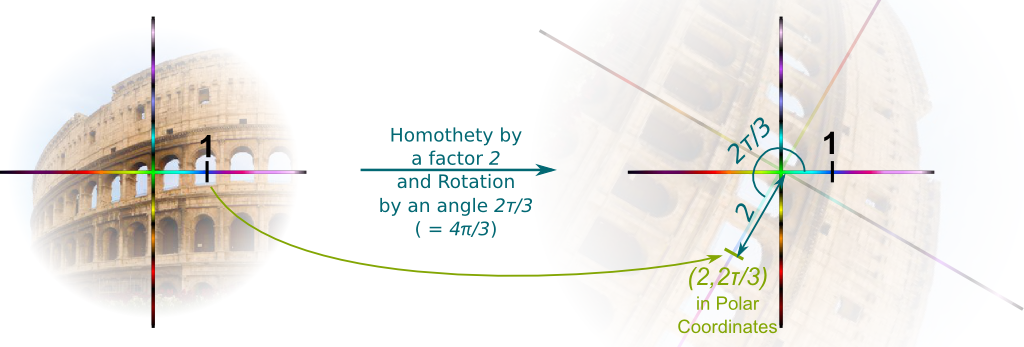
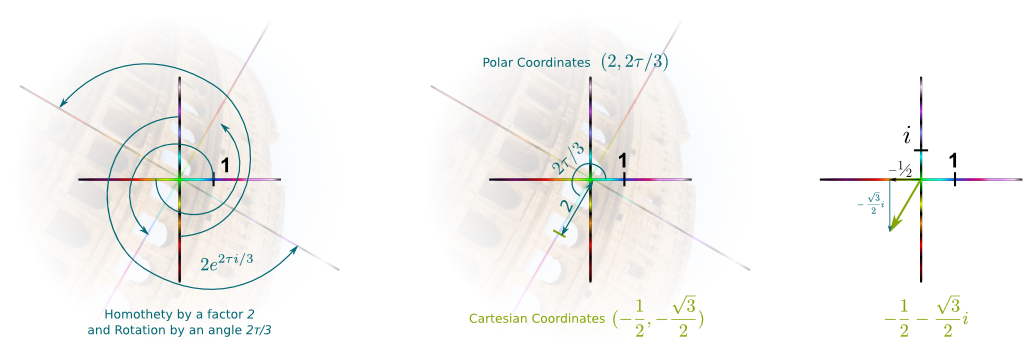
In the 19th century, German mathematician Carl Friedrich Gauss, the Prince of mathematics, provided a powerful visualization of complex numbers. To get there, notice the incredible fact that $1 \times x=x$ when $x$ is a number. Thus, if I show you a geometrical transformation “$\times x$”, then you can easily find which $x$ I chose by looking at what point the number $1$ is sent to. Similarly, if I give you a geometrical transformation $(\rho, \theta)$, then you can find out the values of $\rho$ and $\theta$, as they’ll be the polar coordinates of the point $1$ is sent to! This point is called the image of 1.
Sure! Below is the the combination of a homothety by a factor 2 and a rotation by an angle $2\tau/3$ (2 thirds of a turn).
The factor of homothety $\rho$ is the distance between the image of 1 and the origin, while the angle of rotation $\theta$ is the (anti-clockwise) angle from $1$ to its image.
Exactly! This shows that any geometrical transformation can be translated into a point in the complex plane whose polar coordinates are given by the factor of homothety and the angle of rotation! And this is a one-to-one correspondence between geometrical transformations and points! Thus, we can identify geometrical transformation with points in the complex planes.
Yes! But before doing that, let’s first look to which point of the complex plane the geometrical transformation $i$ is associated to:
I know! What’s also particularly interesting is that we can now describe Euclidean planar geometry with complex numbers!
Vectors in the Complex Plane
To complete the construction of complex numbers, we need to associate any point in the complex plane with a vector.
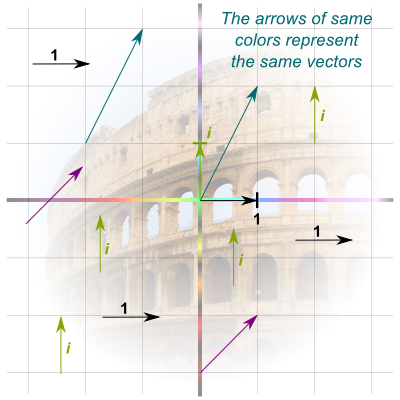
A vector is a motion in the complex plane. This motion is often represented by an arrow from an initial point to a final point. But what’s important to keep in mind is that the vector corresponds to the motion, not the arrow. Two arrows may correspond to the same motion even though they don’t start at the same initial points, as displayed by the arrows of same colors in the figure on the right.
Given a point in the complex plane, we can draw the arrow from the origin to that point. This vector associated to this arrow will then be the vector associated to the point in the complex plane. For instance, $i$ is associated to the arrow from $0$ to $i$, which corresponds to the green arrows in the figure on the right.
We can now define the addition of complex numbers!
By combining the motions associated to the vectors! For instance, combining the purple and green motions is a motion of one unit to the right and by two units upwards. This is equivalent to the blue motion only! This means that $purple + green = blue$. And this can be visualized geometrically by having the purple and blue arrows starting at the same point, while the green arrow is put at the end of the purple arrow. The purple, green and blue arrows must then form a triangle, as done below:
And since all vectors correspond to a complex number, we can now do additions of complex numbers by adding their corresponding vectors!
Now here comes the key part. All vectors can be decomposed uniquely as a sum of $1$ and $i$. For instance, the purple vector can be obtained by a combination of the vector associated to $1$, and a vector associated to $i$. Thus, $purple = 1+i$. Similarly, the blue vector is a combination of $1$ and two times $i$. Hence, $blue = 1+2i$.
Exactly! And since all vectors correspond to a complex number, all complex numbers can thus be written $a+bi$, where $a$ and $b$ are usual numbers. This decomposition enables simple computations of additions of complex numbers! Indeed, if you consider any two complex numbers $z_1$ and $z_2$, then we know by now that each can be decomposed as $z_1 = a_1+b_1i$ and $z_2 = a_2 + b_2 i$. The sum of $z_1$ and $z_2$ is then given by $z_1 + z_2 = (a_1+b_1i) + (a_2+b_2i) = (a_1+a_2) + (b_1+b_2)i$.
This Cartesian description of complex numbers would have been quite useful if it hadn’t been for the more general approach of linear algebra to define vectors.
The Field of Complex Numbers
Let’s sum up what we’ve discussed so far. The awesomeness of complex numbers is that they can be identified with several different mathematical objects. They can be seen as combinations of homotheties and rotations of the complex plane, as points in the complex plane and as vectors in the complex planes. The first understanding of complex numbers describes the multiplication, while the third describes the addition. Thinking about each of the meanings of complex numbers separately is already quite mesmerizing, but the truly mind-blowing property of complex numbers occurs when we mix them!
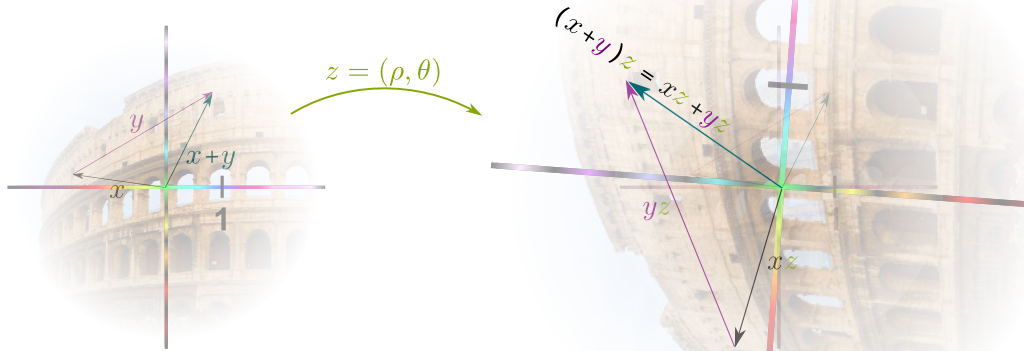
Let’s see what happens when we both have a multiplication and an addition! In particular, let’s focus on the simplest possible case, namely $(x+y) \times z$, where $x$, $y$ and $z$ are all complex numbers.
Well, the expression starts with the addition of $x$ and $y$…
Exactly! Let’s draw $x$, $y$, and their sum $x+y$. But then, we need to multiply these terms by $z$. How do we do that?
Very good! This means that $xz$, $yz$ and $(x+y)z$ will be the image by the geometrical transformation “$\times z$” of $x$, $y$ and $z$. This is what’s drawn below:
Now, the magic occurs when we notice that any geometrical transformation $\times z$ preserves the shapes of triangles. As a result, the triangle $x$, $y$, $x+y$ gets transformed into the triangle $xz$, $yz$, $(x+y)z$. And this means that the sum of the sides $xz$ and $yz$ equals the last side $(x+y)z$! In other terms, $xz+yz=(x+y)z$. This is the essential distributivity property which binds the two operations we have defined on complex numbers! It says that the structure of complex numbers is much richer than the structures of geometrical operations and vectors alone.
What’s awesome about that is that all the algebraic manipulations you could do with usual numbers still hold for complex numbers. In particular, operations like $(x+y)^2 = x^2+2xy+y^2$ are still valid for complex numbers! This strong resemblance of manipulations is what led mathematicians to call complex numbers… numbers. In pure algebra terms, we say that complex numbers form a field.
Conclusion
To recapitulate, a complex number is very complicated mathematical object, which can be seen through diverse angles. Mainly, it can be seen as a combination of a homothety and a rotation, as a point in the complex plane or as a vector of dimension 2. These three interpretations are displayed below.
But what makes complex numbers so special isn’t the different angles through which they can be seen, but the combination of them all, in sort of the same way that quantum objects aren’t simply classical waves nor classical particles. Namely, the full nature of complex numbers is unveiled as they are considered as a field. In particular, it is to that field that the fundamental theorem of algebra gets applied.
This theorem, which was first proven by Carl Friedrich Gauss, states that all polynomial complex equations have solutions. It’s as simple as that. This property is also known as the fact that the complex numbers form the algebraic closure of real numbers. In fact, as mentioned briefly in my article on the construction of numbers, the most insightful and natural (but also terribly abstract) way to construct complex numbers is precisely by defining them as the algebraic closure of real numbers.
Many more equations can now be solved! And I’m not only talking about the polynomial equations. More importantly, natural and simple solutions appear in differential equations, electromagnetism, eigen-value search, Fourier transform and number theory among many other fields. In particular, complex numbers have turned out to be the right structure to describe particle physics! Check my article on the dynamics of the wave function in quantum mechanics to see the complex numbers in action!
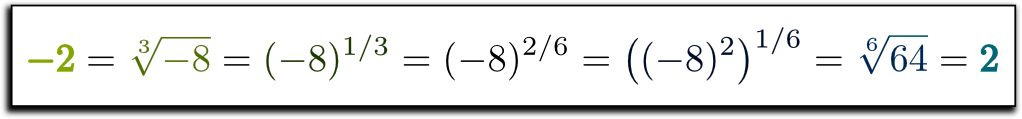

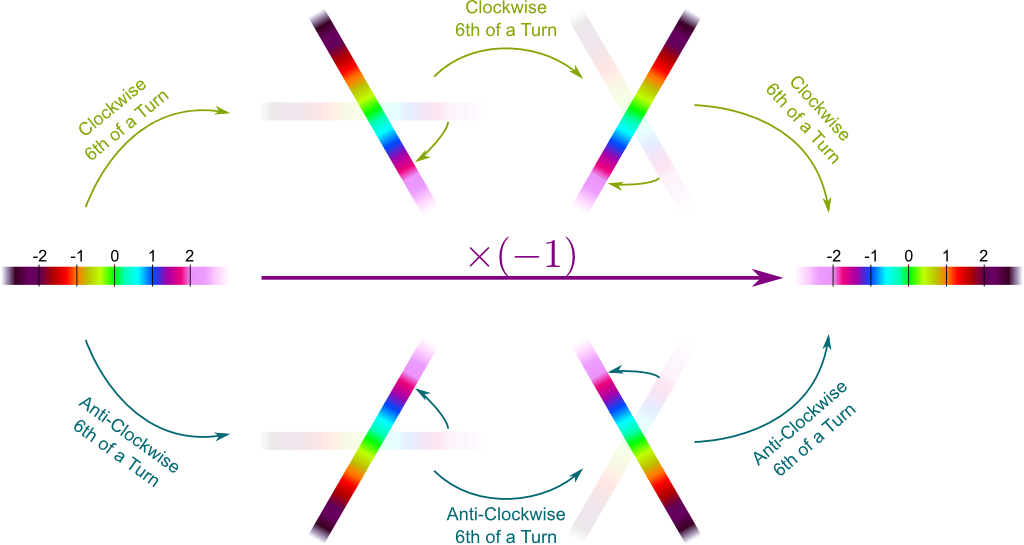

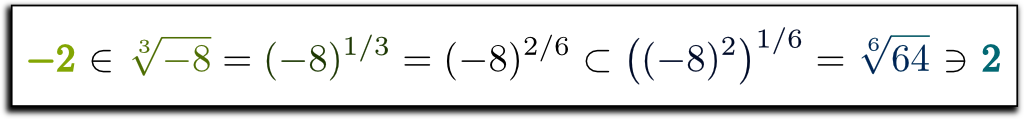
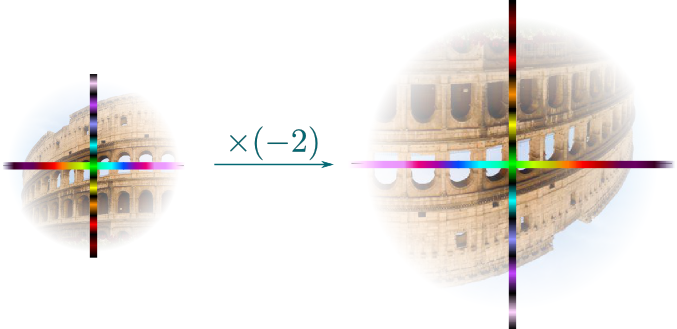
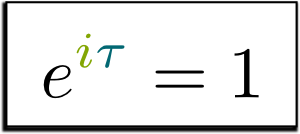


Leave a Reply