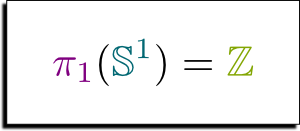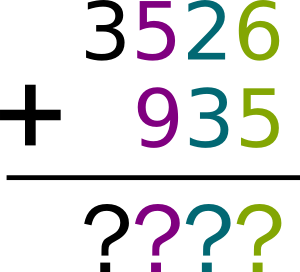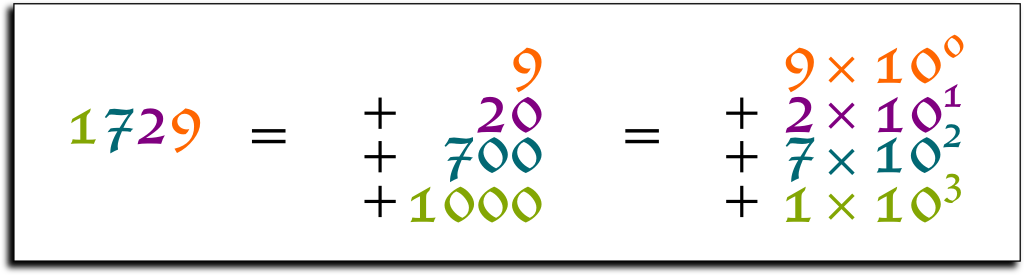In 2013, mathematics was given a reboot by some of today’s greatest mathematicians. The new foundations of mathematics they defined was published in a heavy tome. And there’s definitely more to come, as Carnegie Mellon has just received a 7.5 million dollar DoD grant to further the research area launched by the tome! Amazingly, these new foundations rest upon a single axiom. This axiom, which was proposed by Fields medalist Vladimir Voevodsky, could overturn our intuition of what mathematics is, or, at least, what it should be. In this third episode following my articles on type theory and higher inductive type, we add this axiom to our mathematical universe and gaze at the phenomenal structures that emerge out of it!
Previously, on Science4All…
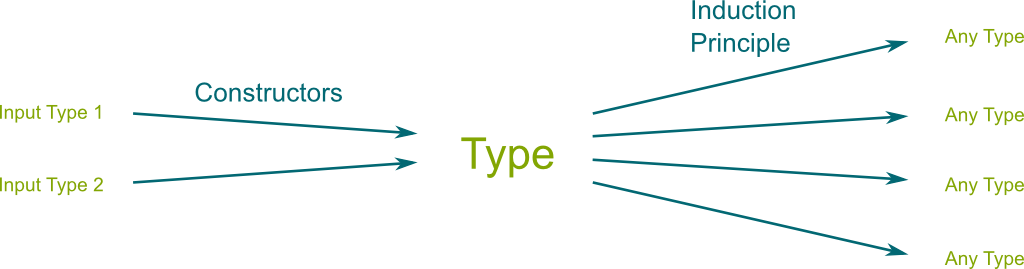
Type theory is a foundational theory of mathematics based on constructions. This means that any term must belong to a type, and it must have been conceived by a constructor of the type. Weirdly enough, this includes proofs. And it works! This perspective on mathematics has enabled to regard the “game” of proving theorems as a game of proof construction, which is amazingly adequate to for computerized proof verifications.
Sure. Let’s reconsider the natural number type $\mathbb N$ I introduced in the first episode. This type has two constructors:
- The zero constructor $0:\mathbb N$.
- The successor constructor $\mathsf{succ} : \mathbb N \rightarrow \mathbb N$.
This means that any term (or inhabitant) of $\mathbb N$ must either be $0$ or the successor of another term of $\mathbb N$. Now, to complete our definition of the type $\mathbb N$, we also need to determine how to construct outgoing functions $f: \mathbb N \rightarrow ?$. This is known as the induction principle. For $\mathbb N$, the induction principle requires the image $f(0)$ of $0$, and the way we construct $f(\mathsf{succ}(n))$ from $f(n)$. For instance, we define the addition $+: \mathbb N \times \mathbb N \rightarrow \mathbb N$ by induction on the first variable, that is, $0+m :\equiv m$ and $\mathsf{succ}(n)+m :\equiv n + \mathsf{succ}(m)$.
As explained in the second episode, one main idea of homotopy type theory is that of higher inductive types. These are types with path constructors, also known as identity proof constructors. For instance, we could define $\mathbb Z/5\mathbb Z$ with the same constructors as $\mathbb N$, and with an additional path constructor that yields $p:5=0$.
Number Systems
The History of mathematics has probably started with the use of numbers to keep track of commercial exchanges. In those days, merchantmen would write down the number of bags of fruits they sold. At first, they would use strokes to count. This pretty much corresponds to our definition of natural numbers: Whenever the merchantman adds a stroke, he’s actually applying the successor constructor to the number he had. The trouble with this number system though is that it’s very wordy. Writing down $1729$ would take forever…
The Egyptians did. And so did the Romans. But their number systems still led to very lengthy numbers:
Our modern number system comes from the Babylonians and, more importantly, from the Indians and the Arabs. This system is based on Arabic digits. I’m not sure you need a reminder, but if you do, you may simply search for “numbers” on Google Image:
We have got so used to our numbers that we forget how unnatural these are. After all, for us, numbers are merely interpretations of finite lists of digits. But, are these really the same as the merchantmen’s and the Egyptians’? Are they the same as the terms of type $\mathbb N$?
To answer that mathematically, we need to model our interpretations of numbers with a mathematical foundation theory. Fortunately, homotopy type theory yields a natural framework to do so. First we need a type $\mathsf{Digit}$ which contains all the digits from 0 to 9. Given it, we now can define a type $\mathsf{List}(\mathsf{Digit})$ of lists of digits, whose terms are constructed by appending (or prepending) digits. Finally, we interpret these lists as numbers of type $\mathsf{Number}$. This means that the type $\mathsf{Number}$ has a constructor that inputs a list of digits to construct a number.
I like your perspicacity! To make sure that $01=1$ as numbers, all we have to do is to add a path constructor that yields a proof that a number defined by a list of digits equals the number defined by this list of digit preceded by the digit 0. Now, for our type $\mathsf{Number}$ to be worthy of that name, we need to define how its terms add up. And, amazingly, this is something we all have learned back when we were kids. Do you remember?
I am! As we’ve all learned it, addition of numbers boil down to operations on the digit lists that represent them. We start by adding units. Then, we move to tens without forgetting the carry over of the units. And we work out recursively this process for hundreds, thousands and so on. If you need a reminder of that, check this awesome Numberphile video with Matt Parker, who’ll explain how to do that with dominos in base 2:
Now, I want you to imagine yourself talking to some Egyptian scholar who’d ask you to add $3526$ and $935$. But obviously, these two numbers would be written down with the hieroglyphs of his number system, and he’d expect an answer written in hieroglyphs too. What would you do?
Well, then, I bet the Egyptian scholar would look at you with big eyes and he’d ask: “How on earth could you possibly have had the right result?”
Equivalence
What you’ll want to tell him is that the number system $\mathsf{Number}$ is equivalent to that of hieroglyphs. Now, because you’re probably not fluent in Egyptian hieroglyphs (shame on you!), I’m going to restrict myself to the equivalence of our number system $\mathsf{Number}$ with the number system $\mathbb N$. After all, it’s a natural and important question to ask. Does the formal number system $\mathbb N$ really match the digit lists we are used to, and vice versa?
To be absolutely sure (that’s the standard of math, right?), we need to prove it.
These questions have become the core of modern mathematics. Ever since the 20-year-old revolutionary Evariste Galois noticed the sameness of diverse symmetries in the early 19th Century, mathematics has been enhancing the importance of defining and detecting the sameness of different mathematical objects, as expressed by Poincaré in the following famous quote:
In our case, what we want to prove is that we can translate numbers in $\mathbb N$ into numbers in $\mathsf{Number}$, back and forth. More precisely, we want a “dictionary” $f : \mathbb N \rightarrow \mathsf{Number}$ that translates numbers of $\mathbb N$ into numbers of $\mathsf{Number}$, and a “dictionary” $g : \mathsf{Number} \rightarrow \mathbb N$ that does the converse translation. What’s more, we want proofs that $f$ and $g$ are consistent translations.
Since, mathematically, $f$ and $g$ are functions, we need to use induction principles. Since $f$ is a dictionary which inputs numbers of $\mathbb N$, we use the induction principle of $\mathbb N$ to define it. This means that we first need to determine the image of $0:\mathbb N$, which will obviously be $f(0) :\equiv 0 : \mathsf{Number}$. Then, we need to choose how to use $f(n) : \mathsf{Number}$ to construct $f(\mathsf{succ}(n)) : \mathsf{Number}$. In other words, we need a function $f_{succ}:\mathsf{Number} \rightarrow \mathsf{Number}$ that will define $f(\mathsf{succ}(n)) :\equiv f_{succ}(f(n))$. That’s easy, as we just need to add 1 to $f(n)$ to have the translation of $\mathsf{succ}(n)$. So, we’ll choose $f_{succ}(x) :\equiv \mathsf{add}(x,1)$, where $\mathsf{add}$ is the addition in $\mathsf{Number}$.
As we’ve all learned it, the number $1729$ is in fact the same as $1 \times 1000 + 7 \times 100 + 2 \times 10 + 9$. More generally, a number written as a string $a_n a_{n-1} … a_2 a_1 a_0$, where $a_0,a_1,…,a_n$ are digits, is in fact the number $a_0 + a_1 \times 10^1 + a_2 \times 10^2 + … + a_n \times 10^n$. We can use this to define by induction the converse translation $g: \mathsf{Number} \rightarrow \mathbb N$.
Next, we need to make sure that the dictionaries $f$ and $g$ are consistent with one another. This means that we need proofs that the translation of a translation gets us the right initial number, from the perspective both number systems. Formally, we need proofs that for all $n:\mathbb N$, we have $g(f(n)) = n$ and that for all $x:\mathsf{Number}$, we have $f(g(x)) = x$. If we come up with such proofs, then the dictionaries $f$ and $g$ are consistent, in which case we say that the functions $f$ and $g$ are equivalences.
To prove that the types $\mathbb N$ and $\mathsf{Number}$ are more or less the same, it suffices to come up with equivalences between them. In fact, we then say that the two types are equivalent. Type theoretically, we denote $\mathbb N \simeq \mathsf{Number}$ the type of equivalences between $\mathbb N$ and $\mathsf{Number}$. A term of the equivalence $\mathbb N \simeq \mathsf{Number}$ is then a proof of this equivalence. Such proof is given by two dictionaries $f : \mathbb N \rightarrow \mathsf{Number}$ and $g : \mathsf{Number} \rightarrow \mathbb N$, and a proof of their consistencies.
There’s a reason why mathematicians use $\mathbb N$ and why we use $\mathsf{Number}$ in our daily lives (and why computers use list of bits). Despite their resemblances, these types are quite different to manipulate. The type $\mathsf{Number}$ is so much more practical to represent numbers, and to do human computations. Lists of bits are the easiest to be manipulated mechanically or electronically. Finally, $\mathbb N$ is by far the easiest to do proofs for! So, it’s common for mathematicians to prove things about $\mathbb N$ and to hint at the fact that they hold for $\mathsf{Number}$ as well, without proving it formally. This leads us to univalence…
Univalence
Over the last two centuries, it has become very common in mathematics to seek and find equivalences between structures, like between $\mathbb N$ and $\mathsf{Number}$. As another example, consider the set $\mathbb Z/12\mathbb Z$ of numbers modulo 12 that represent hours in a half day. In set theory, it is usually formally defined as a partition of integers, whose element are subsets of the form $12\mathbb Z + k$ with $k \in \mathbb Z$. In short, a complicated stuff. But clocks usually identify numbers of this sets with numbers between 1 and 12. Like in real life, this sort of identification is often done informally by professional mathematicians, but rarely formally. This gap between informal mathematics and formal mathematics has been a hurdle to a computable approach to mathematics.
Yes! More precisely, to allow for the identification of equivalent types, Fields medalist Vladimir Voevodsky has proposed to add an axiom to homotopy type theory. This axiom is the single axiom of homotopy type theory. It is known as the univalence axiom. Roughly, it says that equivalent types are propositionally equal. This can be written as $\mathsf{ua} : (A \simeq B) \simeq (A = B)$ for all types $A$ and $B$. In essence, with the univalence axiom, equivalent types may be formally identified… exactly the way mathematicians do it informally!
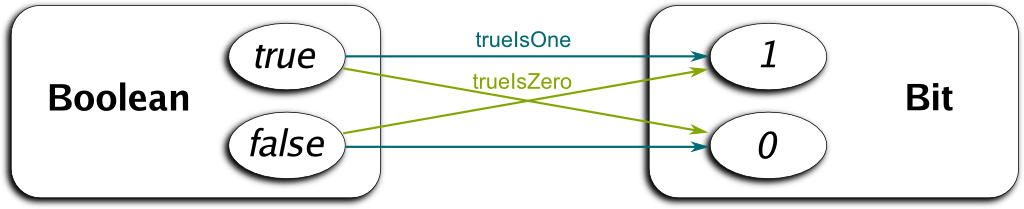
So, if we assume the univalence axiom, we have a proof $\mathsf{ua}(f)$ of the equality $\mathbb N = \mathsf{Number}$. We may also find proofs that $\mathbb Z / 12 \mathbb Z$ equals the type of numbers between 1 to 12. Another important equality derived from univalence is that of booleans (which equal true or false) and bits (which equal 0 or 1).
I guess we could. But proofs of equalities are very practical. For instance, by path induction, we know that, for any function $h$ whose inputs are types, we also have $h(\mathbb N) = h(\mathsf{Number})$. In particular, $h(\mathbb N)$ holds if and only if $h(\mathsf{Number})$ does. Thus, it suffices to use the classical proof by induction on $\mathbb N$ to prove facts about $\mathsf{Number}$ without involving the translation $\mathbb N \simeq \mathsf{Number}$ we defined earlier in the proof!
But univalence isn’t merely a matter of computation. It has beautiful consequences. Most importantly, using univalence, we can prove that there are different proofs of certain propositional equalities.
Let’s get back to booleans and bits. It’s easy to see that there are two ways to translate booleans into bits: Either we translate $true$ by $\mathsf{trueIsOne}(true) :\equiv 1$, in which case we’d necessarily have to define $\mathsf{trueIsOne}(false) :\equiv 0$ (and that’s the most common translation used in computer science). Or, we translate $true$ by $\mathsf{trueIsZero}(true) :\equiv 0$, and complete the translation by defining $\mathsf{trueIsZero}(false) :\equiv 1$. It’s not too hard to see (and prove formally) that $\mathsf{trueIsOne}$ and $\mathsf{trueIsZero}$ are equivalences $\mathsf{Boolean} \simeq \mathsf{Bit}$.
Bear with me. Using univalence, we have two definitionally-different proofs $\mathsf{ua}(\mathsf{trueIsOne})$ and $\mathsf{ua}(\mathsf{trueIsZero})$ of $\mathsf{Boolean} = \mathsf{Bit}$. Now, let’s prove that they are also propositionally different. To do so, we use the fact the function $\mathsf{ua}$ is itself an equivalence whose inverse is $\mathsf{idtoeqv}$. So, if the proofs $\mathsf{ua}(\mathsf{trueIsOne})$ and $\mathsf{ua}(\mathsf{trueIsZero})$ were equal, then applying $\mathsf{idtoeqv}$ to both would imply that $\mathsf{trueIsOne}$ and $\mathsf{trueIsZero}$ are equal too. But then, by looking at the value of these functions for $true$, we’d get $1 = 0$, which is absurd. This proves that $\mathsf{ua}(\mathsf{trueIsOne}) \neq \mathsf{ua}(\mathsf{trueIsZero})$.
The Homotopy Group of the Circle
Now that we know that there may be different proofs of a fact, we can dig into the study of the structures of these different proofs. As we have seen in the previous episode on higher inductive types, by interpreting proofs as paths, we can develop a clean model for homotopy theory. For instance, we may define the (homotopical) circle $\mathbb S^1$ with two simple constructors:
- A base point constructor $\mathsf{base} : \mathbb S^1$.
- A path constructor $\mathsf{loop} : \mathsf{base} = \mathsf{base}$.
The circle $\mathbb S^1$ comes with the following induction principle. To construct an outgoing function $f : \mathbb S^1 \rightarrow ?$, we need to determine the image $f(\mathsf{base})$ of the $\mathsf{base}$, and the image $\mathsf{ap}_f (\mathsf{loop}) : f(\mathsf{base}) = f(\mathsf{base})$ of the $\mathsf{loop}$. Now, in the previous article, I claimed that $(\mathsf{base} = \mathsf{base}) = \mathbb Z$.
Recall that, interpreted homotopically, the type $\mathsf{base} = \mathsf{base}$ contains all paths from $\mathsf{base}$ to $\mathsf{base}$. Intuitively, any such path would consist in looping back and forth along the path $\mathsf{loop}$. Yet, since looping in one direction and then back in the opposite direction is the same as staying at the $\mathsf{base}$, we’d expect paths of $\mathsf{base} = \mathsf{base}$ to be of the form $\mathsf{loop}^n$ for $n : \mathbb Z$. This means that there should be some equivalence $(\mathsf{base} = \mathsf{base}) \simeq \mathbb Z$, in which case, univalence would imply $(\mathsf{base} = \mathsf{base}) = \mathbb Z$.
There’s one big trick and a small one. The big trick is that it’s much easier to prove $(\mathsf{base}=x) \simeq \mathbb Z$ for all $x:\mathbb S^1$, even though we know that $x$ will be necessarily $\mathsf{base}$. That’s because this writing is perfectly suited to apply path induction. This leads us to define the translation $f$ by $f(\mathsf{base}) : \mathbb Z \rightarrow (\mathsf{base} = \mathsf{base})$ defined by $f(\mathsf{base})(n) :\equiv \mathsf{loop}^n$.
The small trick is about the definition of the converse translation $g(x) : (\mathsf{base} = x) \rightarrow \mathbb Z$ for all $x : \mathbb S^1$. Given the induction principle of $\mathbb S^1$, we need to determine $g(\mathsf{base}) : (\mathsf{base} = \mathsf{base}) \rightarrow \mathbb Z$. Yet, we don’t have an induction principle for loop spaces like $\mathsf{base} = \mathsf{base}$. But what we do have is an induction principle for $\mathbb S^1$. So, to define $g(\mathsf{base})$, the small trick is to go through two functions $c : \mathbb S^1 \rightarrow ?$, which will capture the effect of non-trivial paths, and $d: (c(\mathsf{base}) = c(\mathsf{base})) \rightarrow \mathbb Z$, which will translate this effect into an integer. We will then pose $g(\mathsf{base})(l) :\equiv d(\mathsf{ap}_c(l))$ for $l:\mathsf{base} = \mathsf{base}$.
This is where the univalence axiom becomes crucial. With univalence, we have quite a good description of spaces $c(\mathsf{base}) = c(\mathsf{base})$… assuming that $c(\mathsf{base})$ is a type! Indeed, the univalence axiom then gives us an equivalence $\mathsf{ua} : (c(\mathsf{base}) = c(\mathsf{base})) \simeq (c(\mathsf{base}) \simeq c(\mathsf{base}))$!
Now, intuitively, you may notice that $A \simeq A$ is more or less the type of permutations of type $A$, so that if $A$ is finite, so is $A \simeq A$. Thus, intuitively, $c(\mathsf{base})$ must be a type with an infinite number of terms….
Bingo! Let’s choose $c(\mathsf{base}) :\equiv \mathbb Z$. Now, because $\mathsf{loop}$ is a non-trivial path $\mathsf{base} = \mathsf{base}$, we’re going to define its image as a non-trivial loop $\mathbb Z = \mathbb Z$. Using univalence, this means that we need a non-trivial equivalence $\mathbb Z \simeq \mathbb Z$. Any idea?
That’s it! This successor function is an equivalence of $\mathbb Z \simeq \mathbb Z$, since it has an inverse (the predecessor function). Therefore, $\mathsf{ua}(\mathsf{succ})$ is a non-trivial path $\mathbb Z = \mathbb Z$. We may thus choose $\mathsf{ap}_c(\mathsf{loop}) :\equiv \mathsf{ua}(\mathsf{succ})$.
We’re nearly there! We still need a function $d : (\mathbb Z = \mathbb Z) \rightarrow \mathbb Z$. But given an element of type $\mathbb Z = \mathbb Z$, the function $\mathsf{idtoeqv}$ enables us to extract a function $\mathbb Z \rightarrow \mathbb Z$. But then, we may simply extract the value of that function at 0 to get a number of $\mathbb Z$. In formal terms, we define $d(p) :\equiv \mathsf{idtoeqv}(p)(0)$. So, combining it all, we finally obtain the function $g(\mathsf{base})(l) :\equiv \mathsf{idtoeqv}(\mathsf{ap}_c(l))(0)$. And it’s not hard to see that $g(\mathsf{base})(\mathsf{loop}^n) \equiv \mathsf{idtoeqv}( \mathsf{ua}(\underbrace{\mathsf{loop} \cdot \ldots \cdot \mathsf{loop})}_{n \; times} )(0) \equiv \underbrace{\mathsf{succ} ( \ldots ( \mathsf{succ}}_{n \; times}(0))) \equiv n$.
Yes. It is relatively easy to see that $g(x)(f(x)(n)) = n$ for all $n : \mathbb Z$ and $x:\mathbb S^1$, since $f(\mathsf{base})(n) :\equiv \mathsf{loop}^n$, and $g(\mathsf{base})(\mathsf{loop}^n)$ corresponds to applying $n$ times the functions $\mathsf{succ}$ to $0:\mathbb Z$. But what’s more, miraculously, by (based) path induction, the proof of $f(x)(g(x)(l)) = l$ for all $x:\mathbb S^1$ and $l : \mathsf{base}=x$ merely boils down to the simplest case where $x \equiv \mathsf{base}$ and $l \equiv \mathsf{refl_{base}}$. Yet, in this case, it is immediate that $g(x)(l) \equiv 0$ and $f(x)(g(x)(l)) \equiv \mathsf{refl_{base}} \equiv l$, and thus the equality $f(x)(g(x)(l)) = l$ holds trivially! That’s it! We’ve proved that for any $x: \mathbb S^1$, $f(x)$ and $g(x)$ are equivalences! In particular, for $x\equiv \mathsf{base}$ using univalence, we have $(\mathsf{base} = \mathsf{base}) = \mathbb Z$. In homotopical words, we have…
We’ve done it! Woohoo! (Plus, as an easy corollary, we can see that $\mathsf{loop} \neq \mathsf{base}$!)
Conclusion of the Series
In addition to making formal mathematics closer to informal mathematics, the main contribution of univalence to mathematics is to develop a clean model for homotopy theory. As homotopy theory has become a cornerstone of mathematics, this is already very exciting! But there’s more.
Chapter 9 introduces a new way to do category theory using a construction similar to univalence. More precisely, homotopy type theorists propose to only focus on categories whose isomorphic objects are identified. In our example of numbers, this means that we have a path $(\mathbb N, +) = (\mathsf{Number}, \mathsf{add})$ within the category that contains both (say, in the category of groups). This path not only identifies the types $\mathbb N$ and $\mathsf{Number}$, but their additive structure as well. If you want to convince the Egyptian scholar that your trick is consistent with his ways, it’s this identity that you’ll want to show him! Interestingly, such categories with identified isomorphic objects are better behaved than usual categories.
I need to tell you about the last chapter of the book too! It presents a new constructive definition of real numbers. Here’s the trouble with classical real numbers: To assert that they are Cauchy-complete, we need a construction that depends on the (non-constructive) axiom of (countable) choice or the law of excluded middle. Arguably, constructive alternatives often have their own defaults. By proposing a new construction based on higher inductive types, homotopy type theorists may have changed the way we should perceive these complex objects! It is based on the three following constructors:
- A constructor from rationals $\mathsf{rat} : \mathbb Q \rightarrow \mathbb R_c$.
- A constructor from Cauchy approximations $\mathsf{lim} : \mathsf{CauchyApprox} \rightarrow \mathbb R_c$.
- A path constructor for two reals $\epsilon$-close for all $\epsilon : \mathbb Q_+$.
The difficulty though is that we must simultaneously define the concept of $\epsilon$-close, which is essential for the second and third constructors. And the trick is that Cauchy sequences of real numbers already appear in the definition of real numbers… which is weird and is the power of homotopy type theory! Once again, authors of the book argue that we here obtain real numbers which are better behaved than classical ones. And this might fundamentally change a lot of the mathematics we do, especially if we want mathematics to be computable/computerized!