Website dictionaries would define colors with colorless definitions. Yet, colors are a fascinating phenomenon of physics. That’s why, I’ve decided to reveal the colors’ true colors! In order to do that, we’ll have to understand a little bit of physics of light, then we’ll get to human perceptions. Finally, we’ll discuss common representations of colors.
Lights and wavelengths
First, we need to talk a little bit about light. What’s the light?
Well, in fact, it’s more complicated than that, and I would have to talk about electromagnetism to better define what light is. Well, in fact, I don’t actually understand what light really is… However, for our discussion, considering that light is a ray that propagates in straight line is good enough. Well, almost. It’s important to add that a ray of light has also a property called wavelength, usually measured in nanometers (denoted nm), that is one billionth of a meter. To know more about these wavelengths, you can read my article on Fourier analysis.
Because the color of the ray of light depends on the wavelength. In fact, the ray of light will only be seen if this wavelength is somewhere between 380nm and 780nm. And each wavelength in-between can be associated with a color, as shown in the following figure.

Well, not exactly. Carefully observe all the colors. Do you notice something?
Precisely! What’s more all the colors of the spectrum are really pure. There’s no blueish, greenish or redish color… There are no pale colors. There are none of the Science4All colors!
The colors that appear in this spectrum are actually the ones that can be obtained with one ray of light only. They can also be obtained with a beam of light, that is a set of rays, whose rays all have the same wavelength. In this case, we talk about monochromatic beams of light.
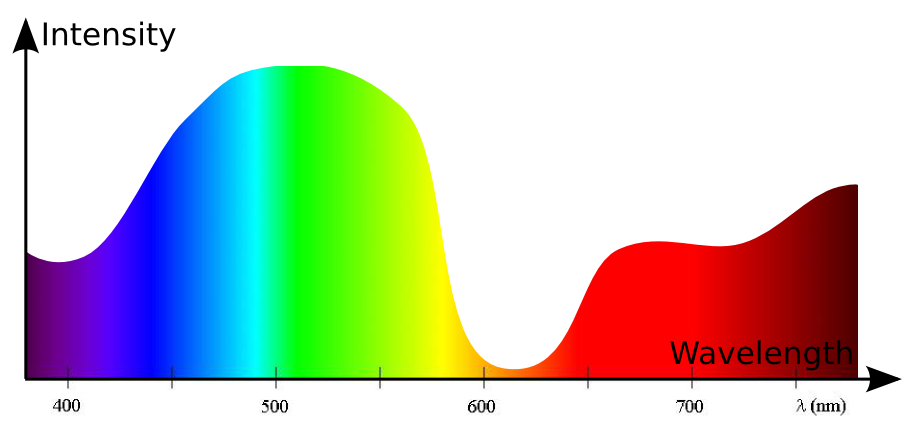
But, as you might have guessed, most beams of light are actually composed of rays of different wavelengths. As there are a lot of wavelengths and as the wavelengths of rays are usually not precise, the best way to model a beam of light is through a distribution of wavelength. The following figure displays a description of a beam of light through such a distribution of wavelengths.
The intensity of a wavelength shown on the figure is related to the number of rays of a given wavelength caught in a second. The more rays of a given wavelength there is, the higher the intensity of the wavelength is.
As you can see on this figure, there are lots of monochromatic cyan and green rays. There are also quite a few of monochromatic purple, blue and red rays. However, there are almost no monochromatic yellow and orange rays. This figure gives a complete description of the colors of the beams.
No. When we watch a beam, we only see one color.
In order to understand that, we’ll now need to study the human eye…
The eye’s perception
What you need to know about the eye is that it captures rays of lights with 4 sorts of captors. One of them, called the rod cell is specialized in low luminosities and does not affect our judgement of colors when luminosity isn’t low. That’s why we won’t be dwelling on the rod cell.
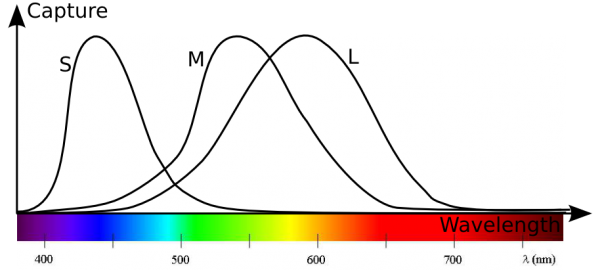
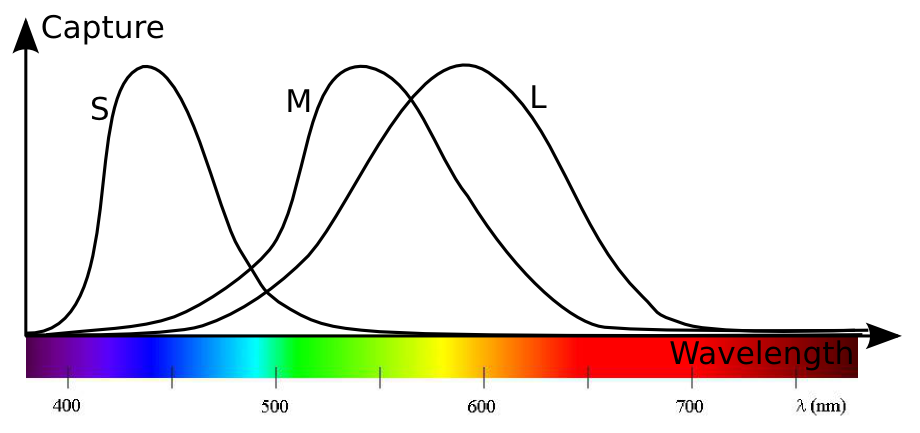
This leaves us with 3 sorts of captors only. They are called cones L, M and S. Each cone is able to capture rays of specific wavelengths, with some wavelengths much better captured than others. It will then transfer to the brain a signal. The more rays it captures, the stronger the signal will be. The following graph shows what proportion of rays of each wavelength is captured by each sort of cone (the graph is an approximation of the real curves of capture).
Note that other species may have more or less sorts of captors. For instance, most mammals except primates are monochromats, that is they only have one sort of captor and therefore don’t distinguish colors. Others have 2, 3, 4 or even 5 sorts of captors like pigeon which are therefore assumed to be able to recognize many more variations of colors.
Exactly. But that’s not all. For a monochrome purple light, not only do S cones send a strong signal, but it’s important to notice that other cones don’t capture any rays.
That’s a great question. Basically the number of monochromatic rays detected by a captor is the multiplication between the intensity of the monochromatic rays and the capture ability of the captor for that monochromatic rays. This gives us the following graphs.
Each black solid curve represents the quantity of rays detected. It’s obtained by multiplying for each wavelength the intensity of the beam of that wavelength by the capture capability of the eye captor. Now the signal that’s going to be sent by each captor is about the area under the black solid curve. In our example, the signal of M will be high, where as signals of S and L will be medium. The following figure the powers of the signals, which we’ll call the SML decomposition.
Yes! At least, that’s the color that the eye sees… But it’s not the color the brain sees! As a matter of fact, the brain has this amazing ability to subconsciously interprete the eyes’ signals so that the recognition of objects becomes easier. Look for instance at Edward Adelson’s optical illusion, and compare cases A and B.
The colors of A and B are actually the same. And our eyes actually see the same colors, in the sense that the signals they send to the brain are the same. However, our brain interpretes these signals to visualize the chessboard. Hence, considering that case A should be darker than case B.
There may be something wrong in their eye captors, maybe one of them is working poorly. It’s also possible that the connection between the eye and the nervous system is bad, or that the brain has trouble interpreting the SML signals. This condition leads to a worse decomposition of beams of light into colors. However, some studies have shown that color-blindness sometimes also led to a more accurate detection of certain objects with similar colors, including animal camouflage.
To answer that question I’ll go further in the analysis of colors by talking about its usual decomposition in computers.
RGB decomposition
Note that our eyes actually perform a color decomposition, as it transforms a distribution of wavelengths into three signals S, M and L. However, this decomposition is generally not used for computers and televisions, who usually prefer the RGB decomposition (or some equivalent decomposition such as YUV, Y’UV, YUV, YCbCr, YPbPr…).
I’m sure you can guess it! When we decompose colors, we usually decompose it into… Red, Green and Blue, right? The story of the RGB decomposition is believed to come from James Clerk Maxwell who enabled colored pictures by taking three pictures with red, green and blue filters.
Not exactly! Otherwise a monochromatic yellow ray would be… black, as none of the monochromatic wavelengths would have been recognized. It’s actually more complicated than that. And it all depends on our eye! As a matter of fact, we’ll find a red, green and blue decomposition equivalent to a beam of light if and only if the signals S, M and L are the same. For instance, in our example, notice that the two following beams give the same SML signal to the eye.
Thus, the RGB beam described just above will be seen by our eye exactly like our initial beam of light. That wouldn’t be the case for eyes with 5 sorts of captors. That wouldn’t even necessarily be the case for eyes with 3 sorts of captors that are not the human eye’s sorts of captors.
Well, that is not really correct. As you can see in our example, the signal L, which supposedly corresponds to red, is higher than signal S, which supposedly corresponds to blue. However, there is a correlation between the signals SML and RGB, which explains this approximation written in other articles. But we don’t actually see the RGB decomposition. What we see is the SML decomposition.
I guess. The good thing about the red and the blue monochromatic rays is the fact that they are at the borders of the spectrum. And the good thing about the green ray is that it pretty much matches the M captor. Any other decomposition is possible but, filtering using Maxwell’s process with other colors wouldn’t yield an approximation as good as for RGB.
It’s due to the fact that the RGB decomposition using filters, when the beam of light is not monochromatic, yields a SML signal that is close to the one we would have got if we looked directly to the original light. Equivalently, the RGB decomposition using filters is close to the RGB signal that has the same SML signal as the original light. This is the case in our example. Still, the SML signal we’ll see with the filters will be slightly different from the initial beam of light, thus the colors will be modified.
They mainly use similar technics as Maxwell’s, although they do use sophisticated post-processing, or not only filter blue green and red. As a result, a yellow monochromatic beam of light might not be detected by cameras, and what our eye considers yellow may turn out to be darker or even black with a camera. In fact, reproducing the actual colors we see is quite complicated, and it hasn’t been done until 2009 PaPaLaB’s camera.
Almost… I’ll do a little bit of mathematics to prove that most colors have a RGB decomposition! Each power of S, M and L can be obtained by making a weighted sum of intensities of red, green and blue. Therefore, there is a linear equation system that links power of S, M and L to intensities of red, green and blue. Since equations are linearly independent (this is easy to prove but a little technical and not very important, so don’t worry if you don’t get it), we can inverse the equations to find intensities of red, green and blue if we know powers of S, M and L. As a result, for any beam of light, we have measures of the SML signal, and we can find a RGB signal that will be associated exactly with this SML signal. This RGB signal will have the same color as the initial beam of light.
Anyways, most colors can be reproduced with a RGB signal, and that’s why we use the RGB modeling for screens.
Well, we have managed to obtain the equivalent RGB decomposition, that is the RGB decomposition that will give the same SML signals. In our example, if the power of green is 100%, then the power of blue would be about 60% and the red about 30%. If we consider that the power of green is 255, then the powers of blue and red would be about 153 and 77. However, we may have other values if we modify the power of the green, like 200, 120 and 60, or 100, 60, 30, or even 0, 0, 0. These values depend on the global luminosity. The color the beam corresponds to is one of the color of the following figure.
Notice that this RGB decomposition is the one used on computers. In fact, on the Internet, each color is associated to a html 6 digits hexadecimal code. The two first digits correspond to the power of red, with FF (256 in the decimal code) being the maximum power of red. The third and fourth digits correspond to green, and the two last ones to blue. So for the maximum luminosity, our color in html code would be 4DFF99. As a matter of fact, 4D in hexadecimal code is equal to 4*16+13=77, which is the power of red, FF to 256, the power of green and 99 to 153, the power of blue.
HSL and HSV decomposition
The remarks we have just made on luminosity have led to other modelings of colors very different from RGB and SML. Mainly, HSL and HSV are now probably the most commonly used. They are both based on a RGB decomposition and re-interpretes it.
Let’s start with L and V. They mean luminosity and value. They both measure the global intensity. However, luminosity is more related with the cumulated numbers of detected rays, that is the sum of luminosities of red, green and blue. When luminosity is high, the color tends to white. The description of the color we used earlier was using this luminosity.
The value highlights the maximum of luminosity of red, green and blue. When it is high, the color is intense, but if there is much more red than green and blue it will be quite red. Not white. As opposed to luminosity, value doesn’t deteriorate the color by whitening it.
As you have guessed, luminosity of values don’t describe the actual color. That’s what H and S do. Let’s start with H, that is the hue. The hue is a complicated concept. Not only does it tell what are the dominant and second dominant colors out of red, green and blue, but it also tells us how much the second dominant color is close to the dominant, compared to less dominant. And it tells us all of that by having a value between 0 and 360! For maximum value of S and V, the following figure describes the colors given in function of the hue.
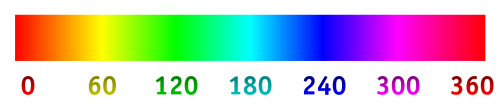
Yes it does. But look carefully. It’s not the same!
Yes. Colors between the red and the blue have been added. But that’s not all. The green and the blue are as far as each other as the red and the green. That’s simply due to the fact that we are reasoning with the RGB decomposition.
This figure can actually be divided into 6 areas, delimited by the numbers. At first, there’s more red than green and more green than blue. Then, more green than red, and more red than blue. Then, more green than blue and more blue than red… and so on. What’s more in the first area, between 0 and 60, the closer we are to yellow, the more the difference between red and green is higher than the difference between red and blue.
Basically, what the hue gives us is the fundamental color we see.
The S stands for saturation. It tells us how big are the differences between dominant colors and non-dominant colors. If this difference is nil (in which case S=0), then there is no difference between dominant colors and non-dominant colors, in which case all red, green and blue are as intense as each other. This corresponds to a grey color. When the difference is big (in which case S=1), the more intense the color we see is, as shown in the following figure where saturation varies from 0 to 1.
In fact, when using Windows’ preview software to view pictures, iPhoto or another software, you can modify the saturation of your pictures very easily, hence making them black and white, or adding colors to them.
Yes. It’s relatively simple (although calculations are required) to go from a HSL or HSV to a RGB signal and vice-versa. And what it tells us is that a color can be understood as a fundamental color (the hue) that’s being tarnished (the saturation) and that has a certain luminosity or value.
The advantage of such a representation is to be less redundant than a RGB signal. Also, we can work directly on luminosity (by modifying it or by changing the contrast) or the saturation. As a matter of fact, image manipulation is more intuitive using this representation. If you know another application of HSL and HSV representations, you are more than welcome to mention it!
Color addition and subtraction
The concept of color primaries is often used to describe colors. As I said earlier, all colors can be obtained using nearly monochromatic beams of red, green and blue. This is often displayed with the following figure.
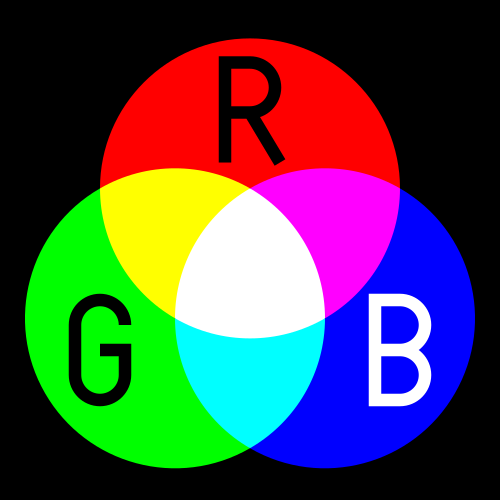
Physically, adding two colors correspond to merging the rays of the two beams of the colors. This concept is not to be confused with mixing colors when painting, in which case we talk about subtracting colors.
To understand that, I need to tell you why the objects we see have their colors. These objects actually absorb some of the light they receive, while diffusing others. There are certain wavelengths that they absorb more, and others that they simply diffuse.
Exactly. Thus, an object receives a beam of light and subtract from it the wavelengths it absorb. This is what happens with paint. Thus, if you paint a wall in red, the paint on the wall will actually be absorbing…
Yes. Now, the subtractive color primaries correspond to the three paints that absorb respectively red, green and blue. The one that only absorb red will diffuse a color that is composed of monochromatic green and blue rays, and will therefore be cyan. The one that absorbs green is equivalent to the addition of red and blue, that is magenta. Finally, the one that absorbs blue is equivalent to the addition of red and green, that is yellow. Any color can almost be obtained with a subtraction of red, green and blue…
Yes! That’s why, to actually have all possible colors we also need the white color, that will diminish the absorption of red, green and blue. Another option, used by printers, is to use bright cyan, yellow and magenta that absorb some of the red, green and blue but not all, and to darken the color if necessary with black.
Subtractive colors are usually displayed with the following figure.

Let us notice however that subtracting yellow and cyan will not always give green. As a matter of fact, yellow can be obtained by filtering it into a RGB decomposition and then deleting the blue component. But it can also be obtained by deleting all components but yellow. Similarly, cyan can be obtained by deleting all components but cyan. But if we subtract all components but cyan to a monochromatic yellow beam, then we’ll have deleted all rays… hence leaving us with a black color. That’s why subtraction of colors is actually more complicated. The figure above does work for the paint colors that we buy, but it may not work with any paint colors.
Let’s sum up
This study of color enhances how good our brain is. It makes so many subconscious operations on our eyes’ signals that we actually have trouble to understand them. It took scientists quite a while to finally understand the true nature of colors, and reproducing these colors is still very difficult.
A color is a measure of a beam of light made by our eyes. What’s interesting to notice is that different beams of light may have the same color. A monochromatic yellow beam of light is therefore, to our eyes, equivalent to a mix of monochromatic red and green beams of light. More generally, our captors are not able to measure the entire nature of the physics of light. If you think about it, even using instruments we may never be able to measure some features of physics. Suppose we knew all the possible measures of the universe. Then there may be several theories that eventually describe all the observed phenomena, and there would be no way of deciding which theory actually corresponds the universe. What we’ll be able to say though is that they all perfectly model the universe. The best one to use to analyze and predict phenomena will be the most simple one. This justifies the “simple is sexy” approach in physics.
I’ll go even further. Plenty of theories may describe “well enough” a set of observed phenomena, just like using RGB decomposition with Maxwell’s filtering process is “good enough” to describe colors. These theories, even though we know they are wrong, may be much more useful than theories that exactly describe the phenomena. That’s why, for instance, Newton’s theories are still very useful, even though we know they are wrong.






Leave a Reply to Lê Nguyên Hoang Cancel reply