The Harmonious Mathematics of Music

According to legend, the Ancient Greek Pythagoras was once walking on the streets of Samos, when the sounds of blacksmiths’ hammering suddenly gave him an epiphany. Pythagoras rushed into the shop and, as he analyzed mathematically the shapes of the blacksmiths’ hammers, he laid the foundations of music that today’s Rihanna, Shakira and others are building upon.

I am. And despite what you’ve learned at school, this Pythagorean theorem is absolutely not Pythagoras’ greatest idea — most notably because he probably wasn’t even the one who came up with the Pythagorean theorem. At least, that’s what I think: Pythagoras’ greatest idea was the mathematization of music, whose harmonious structures would later be the playground of the greatest musicians like Ludwig van Beethoven (we’ll get there!), or like the brilliant mathemusician Vi Hart:

The Perfection of Octaves

As the story goes, when Pythagoras started to play with hammers, he noticed that two of them were particularly harmonious with respect to one another. He measured the weights of these hammers and found out something absolutely startling.

The heavier of the two hammers was exactly twice the weight of the lighter one! Exactly twice.

I know! What were the odds? Pythagoras had focused on these hammers solely because of musical aesthetic considerations. And yet, out of this personal taste of musical harmony, emerged a perfect ratio of 2.

I know! In fact, it was so neat that Pythagoras went on claiming that whole numbers ruled the world… which apparently led his “philosophy school” to drown Hippasus of Metapontum, because Hippasus was claiming to have found some non-perfect-ratio number in the supposedly perfect realm of geometry!

To understand this ratio, Pythagoras turned his attention to the simplest musical instrument: A string. Could it be that the ratio of 2 applied to the string also allow for some musical harmony? Is there harmony between the vibration of the string and, say, the vibration of half of the string?

There is. Today, this essential harmony is called an octave. In fact, octaves are so important in music that we gave the same name to two notes separated by an octave. You know? $A$, $B$, $C$, $D$, $E$, $F$, $G$… Two $C’s$ are separated by exactly an octave. If they are notes played by a string, one corresponds to a string exactly twice the length of the other.

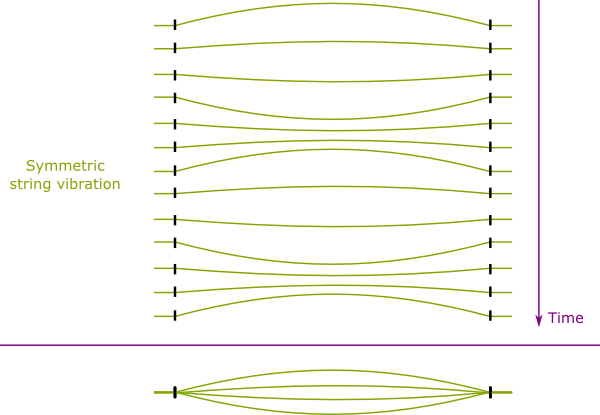
There is! Let’s take the longer string. Let’s say it plays a $C$. It will be a low-pitch $C$. Now, if you pinch the string in the middle, the string will vibrate in a sort of perfectly symmetric way.

But if you don’t pinch it in the middle, it will vibrate in a much more complicated way. A very nastily complicated way. But there’s one thing we do know about the vibration of the string…

End points of the string are fixed. And that’s very important.

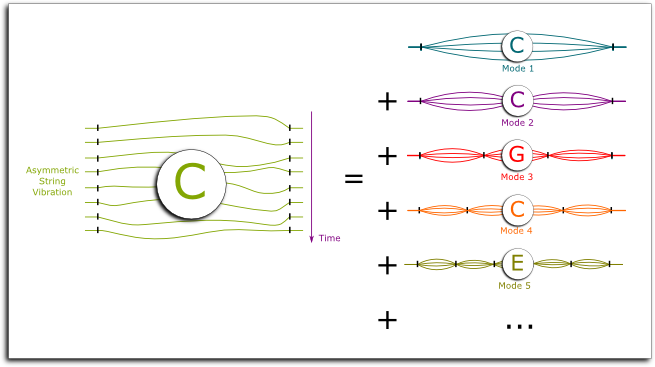
The only symmetric vibrations that leave end points fixed are vibrations that perfectly divide the string in portions of equal lengths. These are called harmonics of different modes. And amazingly, we can prove mathematically that any asymmetric vibration of the long string is the sum of the vibrations of the harmonics.

Now, as you can imagine, unless you pinch the string at its extremity, the higher harmonics will not be loud enough to be heard. In fact, we’ll mainly hear the harmonics of modes 1 and 2.

Exactly! And that’s the reason why two $C’s$ sound so harmonious: The low-pitch $C$ also “plays” the higher-pitch one. It sort of contains it, and thus, when we move from one to another, our ears detect some harmonious continuum.

Let’s Create the Notes

Evidently, if music was only made of octaves, it’d be a bit boring. It’d be pleasing, but a bit monotone. To go further we need to create new notes. And we’ll do that solely based on requirements of harmony.

Let’s consider one string of reference, and let’s say it plays the fundamental note called $0$. We’ve seen that by halving the length of the string, we could define other notes in perfect harmony with the fundamental $0$. And as we’ve said it, these other notes that differ from $0$ by octaves are called $0’s$ as well. More formally, taking higher and lower octaves define all the notes $0’s$ of music.

But music isn’t made only of $0’s$. We need more notes. How can we create them through a coherent mathematical process?

Bingo! As we’ve seen earlier, when $0$ is played, we hear all its harmonics. Moreover, the harmonics that we will hear the most will be those of smaller modes. Now, as we’ve seen modes 1 and 2 are $0’s$. Next is mode 3. This mode 3 harmonic is not any octave higher, so it is not a $0$. It has to be a new kind of note. Let’s call it the note $1$.

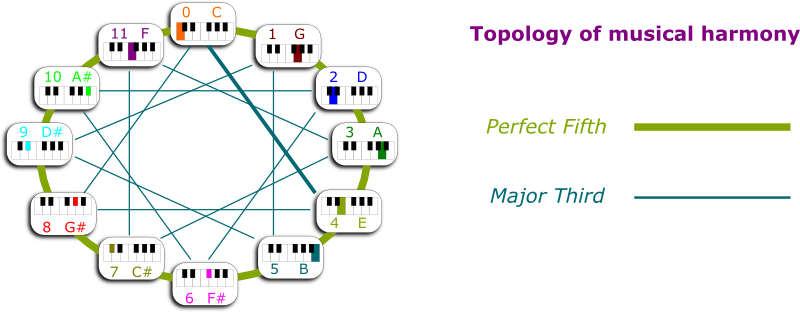
Crucially, the note $1$ is contained within $0$. When $0$ is played, we hear $1$. And that’s why the two notes are harmonious. Musicians say that $1$ is the perfect fifth of $0$.

Let’s listen to this video. The author of the video first plays a series of octaves, and then a series of perfect fifths.

I’ll get to that later (I personally would rather call it a perfect third…). Now that we have one new note $1$, we can also create all notes $1’s$! How?

Exactly!

It’s an awesome observation you’ve just made. In fact, that’s how we can create all the notes of music: We just make up the perfect fifth of the last note we’ve created, and its octaves as well! Thereby, we construct $2$ as the perfect fifth of $1$, $3$ as the perfect fifth of $2$, and so on.

In principle, it shouldn’t stop. We should be creating infinitely many notes!

That’s a good point.

The Impossibility Theorem of Music

We should have a finite number of notes. But that can only happen if some note $n$ we’ve created is the “same” as the note $0$. More precisely, $n$ must be is some octaves higher than $0$.

Unfortunately, it’s not too hard to prove mathematically that this can’t be. This is what could be called the impossibility theorem of music: Perfect harmony in music requires an infinite number of musical notes.

Any note we’ve created is obtained by repeatedly taking thirds. In fact, the note $n$ corresponds to a string of length $1/3^n$ of the original string. Moreover, its $k^{th}$ lower octave is obtained doubling $k$ times the length of the string. Thus, the $k^{th}$ lower octave of note $n$ corresponds to a string length that is $2^k/3^n$ of the original string.

Exactly! In other words, we must have $2^k = 3^n$. But unfortunately, this can’t be. This equation has no solution.

The left term $2^k$ is even but $3^n$ is odd. An even number can’t be odd…

Before telling you what we can do, let me state the impossibility theorem of music.

The Fundamental Theorem of Music

Here’s a positive breaking news though. Despite the impossibility theorem, musicians still manage to play pretty good music.

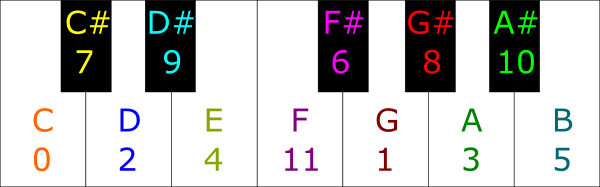
Do you know how many notes there are in an octave?

Are you sure? Aren’t you forgetting some?

It is, isn’t it? This means that something has happened when the note $12$ has been created. This note $12$ corresponds to dividing the string length by $3^{12}$. This is $3^{12} = 531441$. Yet, we also have $2^{19} = 524288$. The ratio of these equal $2^{19}/3^{12} \approx 0.987$. That’s almost 1!

Exactly. In fact, I’d call the approximate equality $2^{19} \approx 3^{12}$ the fundamental theorem of music. Stated differently, it says that the note $12$ is nearly the same as $0$. And all of music has built upon this fundamental approximation, sometimes known as the Pythagorean comma.

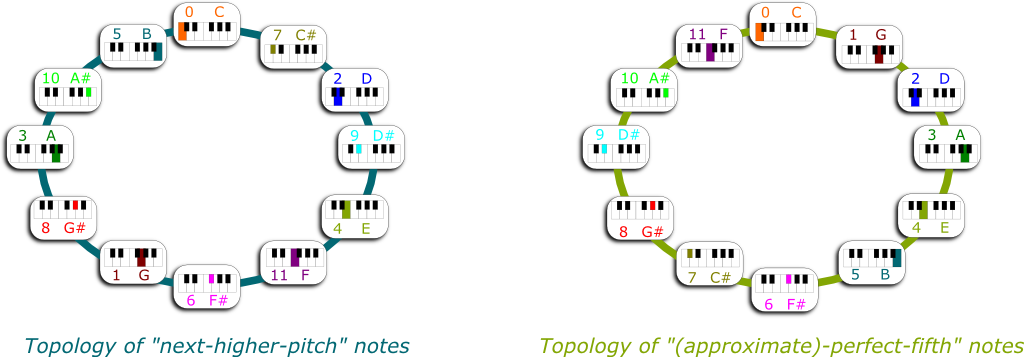
Now that we have 12 notes, we should all order them not only according to harmony as we have done, but according to how they fit in a single octave. I spare you the computations, but we can see that the note of slightly higher pitch than $0$ is $7$, then $2$, $9$, $4$, $11$, $6$, $1$, $8$, $3$, $10$, $5$. And then we’re back at $0$.

Look carefully. It’s not a random list at all. There’s a neat underlying structure. From a note to the next one, either you add 7 or you subtract 5.

Now, this gives us two different ways of ordering the notes of music. We can either order them by pitch proximity in an octave, or we can order them by harmony of perfect fifth:

Finally, I can explain why the perfect fifth is called that way. As you can see in the figure, between the note $n+1$ is always 5 notes after the note $n$. That’s why we say that $n+1$ is the perfect fifth of $n$.

The Second Theorem of Music

One thing that troubled me early on when I heard about music theories was the idea of chords. Some triplets of notes sound good, while others sound terrible. I always thought that this was because of our education: Good music always aline good-sounding triplets, and I thought that repeatedly hearing them led us to like them. But I’ve since stumbled upon a more fundamental explanation which I find fascinating.

The most famous of all chords is the major triad. An example of a major triad is the $C$ major chord. The $C$ major chord plays $C$, $E$ and $G$. This major chord is music’s most celebrated chord. And with reason. It does sound extremely harmonious, as opposed to other random choices of three notes.

Hehe… Remember how a vibrating string can be decomposed into modes?

So, say mode 1 is $C$. Then, mode 2 is…

Yes! Mode 3 is…

Very good. What about mode 4?

Excellent! And now… what about mode 5?

Humm… Is it?

Well, let’s compute it! Recall that $E$ is what we constructed as the note $4$. So, the length of the string it corresponds to is $1/3^4$ of $C$. Let’s now consider the octave 4 times higher. It corresponds to a length of $2^4/3^4$ of that of $C$. Well, $2^4/3^4 \approx 0.198 \approx 0.2 = 1/5$. Do you know what that means?

Exactly!

In other words, when we play $C$, we also hear its modes 2, 3, 4 and 5, which corresponds to $C$, $G$, $C$ and $E$. By playing C, G and E, we are amplifying the notes that we were already hearing! That’s why the major chord is so harmonious!

I know! In fact, the intricate relationship between $C$ and $E$ has been given a name. $E$ is called the major third of $C$. This means that there are more intricate harmony relations between the musical notes, through this major-third relation.

It’s a tricky one. The minor chord consists of replacing the major third by another note called the minor third. The minor third of the note $0$ is the note $3$. But this minor third does not correspond to any mode. It is a bit less harmonious. But disharmony, or dissonance, may lie at the core of the compositions of the greatest musicians. At least, this is what argued for Beethoven by Natalya St. Clair in the following awesome TedEd video:

Let’s Conclude

There’s a cliché out there according to which the mathematical study of artistic phenomena leads to some deterioration of artistic beauty. I strongly feel that this is completely false. In fact, my personal experience has repeatedly been exactly the opposite. It was rather when I learned about the underlying science or mathematics of arts that I started to appreciate artistic masterpieces the way they deserve to be appreciated. This has been totally the case with my appreciation of music. Maths only adds to the musical experience. And, for me, it adds a lot!

I’m telling you! But if you don’t trust me, please listen to the scientist that probably conveyed this idea the best, the great Richard Feynman:

Similarly, I have times and times again been terribly excited by artistic masterpieces whose mathematical structures I could understand. This was especially the case when I stumbled upon a piece of work by François Morellet, when I discovered the fractal nature of Jackson Pollock’s paintings or Escher’s brilliant use of hyperbolic geometry. Seriously, learn the maths, and you will see the whole world through much more exciting perspectives!