In 1988, a Mathematical Intelligencer poll voted Euler’s identity as the most beautiful feat of all of mathematics. In one mystical equation, Euler had merged the most amazing numbers of mathematics: $e^{i\pi}+1=0$.
We’ll get there. But first, I want to insist one more time on the spectacular beauty of Euler’s identity. A recent study showed that Euler’s identity is so beautiful that it excites the same areas of the brains as a great piece of music or art would! If you don’t believe me, listen to the amazing William Dunham tell you about that:
The Dream Team of Numbers
To fall in love with a story, you need to intimately know its characters. So, before talking about Euler’s identity, let’s draw portraits of the dream team of numbers that makes it up. Starting with the most important of them all, the $wau$ number, as presented below in this awesome video by ViHart:
The $wau$ number is amazing, because it usually is the solution of equations in such an obvious way that we even forget it is! For instance, $wau$ is the only solution to the equations $(x^2)! = x$ and $x^x = x$.
Yes! And Historically, $wau$ is the first number invented, making it the father of all mathematics! For this mere reason, wouldn’t you agree to say that $wau$ is just such a more awesome name than 1?
Let’s move on. Surprisingly, the second number to join the dream team is not $0$, but $\pi$. Yet, the number $\pi$ is actually a beautifully evasive number! $\pi$ first appeared in Antiquity, at least several millenia before our era, as the area of a disc of radius 1, or as the ratio of the circumference of a circle by its diameter. Thus, $\pi$ is the symbol of geometry.
Because it wasn’t until the 18th century that some basic properties of $\pi$ were discovered, like the fact that it is irrational. This means that $\pi$ cannot be written as the ratio of two numbers. A century later, it was then proved to even be transcendental, which means that $\pi$ is somehow beyond the realm of algebra.
But, overall, the most important fact about $\pi$ is the fact that it has become a cultural symbol, as explained in this fun Math Bites with Danica McKellar on Nerdist:
While wau and $\pi$ are both ancient numbers, the other numbers of Euler’s identity are more recent. The number $0$ was only invented around the 7th Century in India. It is often attributed to Brahmagupta. And it deeply revolutionized our perspective on mathematics and numbers, as explained by the amazing Marcus du Sautoy in the BBC show Story of Math:
One important aspect of the invention of 0 was the natural extension of numbers to relative numbers. By then introducing negative numbers, the Indians developed the ideas of debts and investments, which were certainly a major and powerful economical innovation. In fact, 0 can be regarded as the father of algebra.
The number $i$ is famously known as an imaginary number. Now, many would argue that this is a horribly wrong terminology, as $i$ occurs in so many areas that it is certainly not more imaginary as “real” numbers like $\pi$. And I agree. In fact, some modern mathematicians like Norman Wildberger argue that $i$ is way more “real” than $\pi$! In any case, the reason why I still find the terminology appealing is that the invention of $i$ has coincided with the (re)birth of pure mathematics.
Historically, algebra was imported in Europe from the Muslim empire. But algebra wasn’t merely a powerful tool for engineers. It was also a perfect language to pose new abstract problems, like that of solving equations. And, amazingly, abstract equations like $x^2+1=0$ naturally led mathematicians to invent a number whose square would be $-1$. This number, sometimes abusively denoted $\sqrt{-1}$, is precisely $i$.
At first, yes. Yet, surprisingly, notably because of Euler’s identity, the number $i$ now plays a central role in many fields, especially physics and engineering, as explained by the two following professors on Sixty Symbols:
Finally, last but not least, is Euler’s number $e$.
Not at all! The reason why Euler introduced $e$ was rather to describe the natural phenomenon of 100% continuous growths.
Imagine you put 1 dollar in your bank, and they tell you’ll win a 100% interest rate every year. Now, because they are crooks, they’ll only compute your interest rate at the end of the year. Thus, you’ll get 1 more dollar, and obtain a total of 2 dollars.
Because they waited for the end of the year to compute your gain! Instead, you may want to argue that the investment rate should be computed every month. Now, because it’s a 100% interest rate in twelve months, and because $100/12 \approx 8.33$, you should get an 8.33% rate every month. And if you do, amazingly, at the end of the year, instead of ending up with 2 dollars, you’ll have 2.61 dollars!
But wait! You can do even better by computing investment rates every day. Or even, every hour. Or every second. Eventually, by having a continuous growth, you would end up with $e \approx 2.718$ dollars at the end of the year. That’s how much you win a year with a 100% continuous growth.
More formally, the 100% continuous growth means that $e$ satisfies the differential equation $e^x = d(e^x)/dx$, and our approach proves that $e = \lim (1+1/n)^n$. These facts make $e$ the symbol of calculus.
Exactly! Let’s sum it up:
Now, to think that all these guys, despite coming from diverse areas of mathematics, manage to merge together and form a breathtakingly neat equation… This really is mind-blowing! And it explains why Euler’s identity is so often regarded as the greatest feat of mathematics!
The Intuitive Proof
Before getting to Euler’s original proof, let’s see the intuition underlying Euler’s identity. But to get there, I need to get you familiar with two major mathematical objects: The complex plane and derivatives.
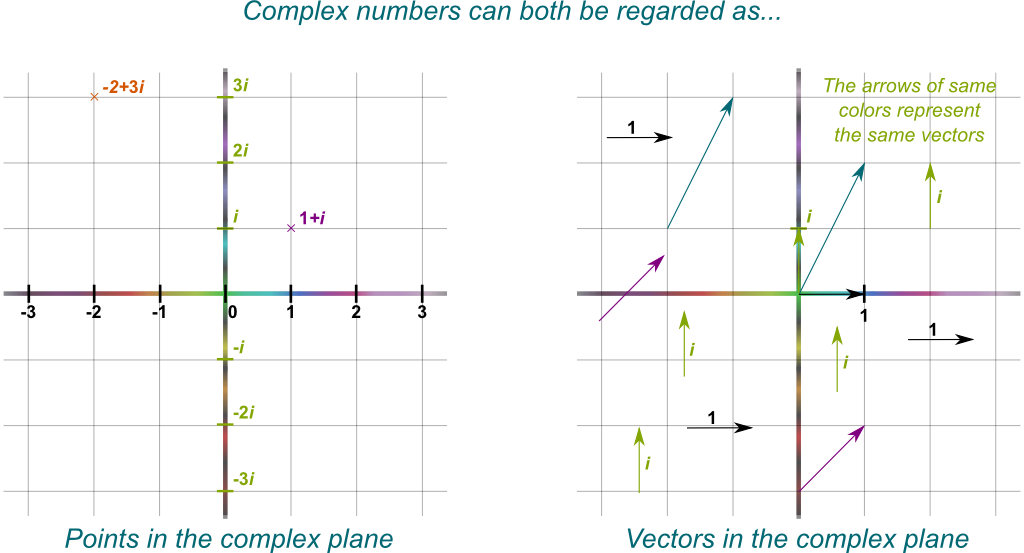
Let’s start with the complex plane, discovered by the giant Carl Friedrich Gauss a century after Euler’s time. Amazingly, while real numbers are points on a 1-dimensional line, imaginary and complex numbers perfectly correspond to points in a 2-dimensional plane. Indeed, a complex number can always be written uniquely $a+ib$, where $a$ and $b$ are the x and y-coordinates of the corresponding point.
A complex number can also be regarded as a motion, or vector, from the origin to the point it represents. This is important to understand the one last thing you need to know about complex numbers: Multiplying a complex number by $i$ corresponds to rotating the corresponding vector by an anti-clockwise quarter of turn. This will be essential in a bit…
Derivatives describe motions, and they’re particularly visual when we consider trajectories in the complex plane.
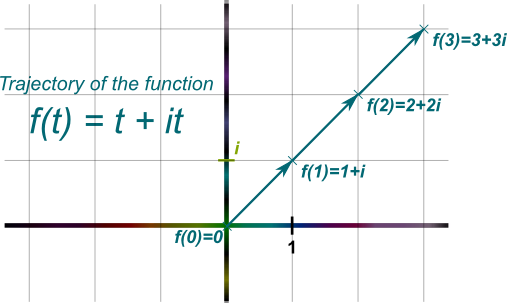
A trajectory corresponds to a function $f$ which maps times $t$ to positions $f(t)$ in the complex plane. By varying $t$, the point $f(t)$ will be describing a trajectory in the complex plane. For instance, if $f(t) = t+it$, then $f$ will correspond to the trajectory that goes along the main diagonal at a constant velocity.
So, really, a function which maps real numbers to complex numbers is just a trajectory in the complex plane.
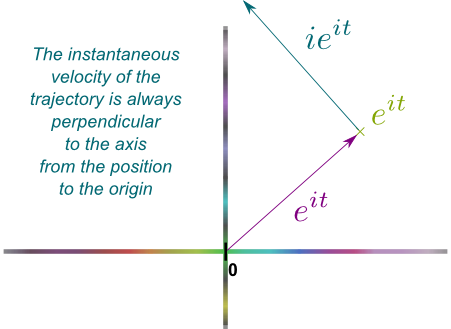
Following Newton’s footsteps, the derivative of a trajectory at a given time is its instantaneous velocity at that time. So, for instance, in the figure above, at any point, the instantaneous velocity is a motion going diagonally up-right. In fact, you may guess that it equals the vector $1+i$, as, in one unit of time $t$, the trajectory moves by $1+i$. Amazingly, this can also be deduced from basic laws of derivation.
You’ve probably learned that the derivative of $\alpha t$ is $\alpha$ when $\alpha$ is a real number. Well, guess what, the same formula holds when $\alpha$ is a complex number! So, the derivative of $f(t) = t+it = (1+i)t$ is…
And now we’re getting closer and closer to proving Euler’s identity! As we have seen earlier, the fundamental property of Euler’s number $e$ is that the derivative of $e^t$ is $e^t$. Now, using the laws of derivation, it must be that the derivative of $e^{it}$ is $ie^{it}$.
Exactly! So, at a time $t$, the trajectory $e^{it}$ is at some point $e^{it}$ of the complex plane. Yet, $e^{it}$ is also the vector from the origin to $e^{it}$. Therefore, $ie^{it}$ is a vector perpendicular to the axis between the origin $e^{it}$ and 0, in the anti-clockwise direction. I know… it’s hard to read. So let me draw this:
Now, if you have done some physics, you should immediately be able to figure out what kind of trajectory $e^{it}$ is.
What if I told you that the origin was the Earth?
Exactly! Just like the Moon, the velocity of the point $e^{it}$ always points perpendicularly to the axis Earth-Moon. And as a result…
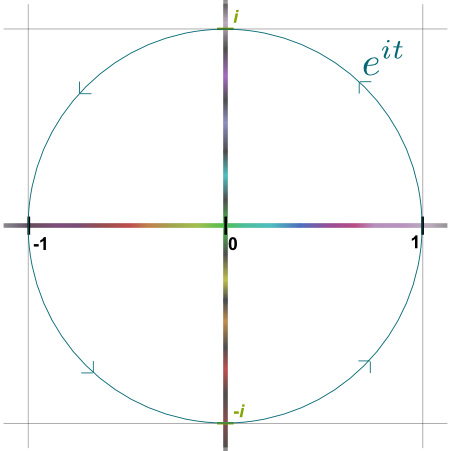
Bingo! The trajectory of $e^{it}$ is that of a circle rotating anti-clockwisely!
Now, since $e^{it}=e^0 = 1$ if $t=0$, this means that this circle must go through 1. It’s thus necessarily the unit circle! Plus, since the velocity of the trajectory is the rotation of the vector $e^{it}$, the speed equals the length of the vector $e^{it}$, which is the radius of the circle: 1. Thus, the trajectory $e^{it}$ is a anti-clockwise rundown of the unit circle at speed 1. How beautiful is that?
I know! And it enables to easily deduce the formula $e^{it} = cos(t) + i sin(t)$. But, we don’t even need that to derive Euler’s identity… What happens when $t=\pi$?
Recall that at $t=0$, the trajectory $e^{it}$ started at 1. Now, it moves at speed 1 along the unit circle anti-clockwisely. So, at $t=\pi$, it will have walked a distance of $\pi$ on a circle of radius 1…
Exactly! This is where the geometry of the circle has $\pi$ entering in play! So, amazingly, $e^{i\pi}$ is the antipode of 1 on the unit circle, which is -1. Thus, $e^{i\pi}=-1$. Or, equivalently, we obtain the beautiful Euler identity:
Euler’s Proof
Now, this insightful and intuitive proof wasn’t Euler’s. Rather, Euler is known for his mastery of infinite sums, which he used to derive his identity.
The key objects of Euler’s proof are power series. A few decades before Euler, British mathematicians Brook Taylor and Colin Maclaurin found out that many real functions $f(t)$ could be written as an infinite sum of powers of $t$. In fact, in many cases, the derivatives of $f(t)$ at $t=0$ were sufficient to describe $f$ everywhere as such a sum. Denoting $f^{(n)}(0)$ the $n$-th derivative at $t=0$, the Taylor-Maclaurin series could then be written as follows:
Now, given that the derivative of $sin$ is $cos$, that the derivative of $cos$ is $-sin$, that $sin(0) = 0$ and that $cos(0) = 1$, we have:
- $sin(0)=0$, $sin^{(1)}(0)=cos(0)=1$, $sin^{(2)}(0)=-sin(0)=0$, $sin^{(3)}(0)=-cos(0)=-1$, $sin^{(4)}(0)=sin(0)=0$…
- $cos(0)=1$, $cos^{(1)}(0)=-sin(0)=0$, $cos^{(2)}(0)=-cos(0)=-1$, $cos^{(3)}(0)=sin(0)=0$, $cos^{(4)}(0)=cos(0)=1$…
Thus, the Taylor-Maclaurin series of the sine and cosine functions are the following ones:
Furthermore, we need to remark that if the derivative of $e^t$ is $e^t$ and if $e^0=1$, then, necessarily, all derivatives at all orders of $e^t$ in 0 must equal $e^0=1$. Thus, the Taylor-Maclaurin series of the $e^t$ is:
Euler’s great move was to then replace $t$ by $it$ in the formula above. By then separating real parts from imaginary parts (I mean terms with $i$), magically, the expression of $e^{it}$ perfectly decomposes itself into $cos(t) + i sin(t)$. I’m a bit lazy so I won’t do that myself, but I’ll let this awesome video by VeritySeeker show it to you:
So, we have $e^{it} = cos(t) + i sin(t)$. By setting $t=\pi$, and given that $cos(\pi)=-1$ and $sin(\pi)=0$, we end up with $e^{it} = -1$. Or, equivalently,
Let’s Sum Up
Euler’s identity is the greatest feat of mathematics because it merges in one beautiful relation all the most important numbers of mathematics. But that’s still a huge understatement, as it conceals a deeper connection between vastly different areas that Euler’s identity indicates. Above all else, Euler’s mystical identity is a clever insight into the perfection of the unit circle, by combining complex and diverse subfields of mathematics! In fact, the countless properties of this perfect unit circle are the reasons why Euler’s identity has become essential in many applications, like in physics.
Yes! And that’s strongly related to the unavoidable Fourier analysis. In essence, Fourier’s mind-blowing discovery is the fact that a large class of trajectories in the complex plane corresponds to infinite additions of unit circles run over at different speeds and in both directions. In calculus terms, this means that many functions $f(t)$ which map real to complex numbers can be written $\int g(\omega) e^{i\omega t} d\omega$, where $\omega$ is the speed of the rundown of unit circles. One important application of that is for the understanding of resonance.
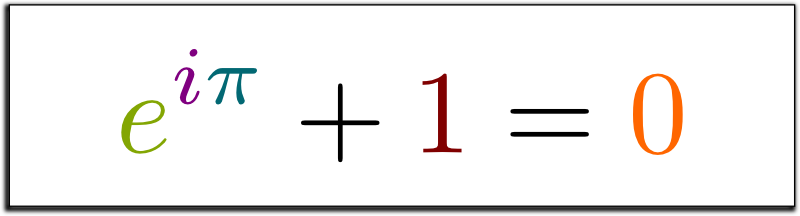
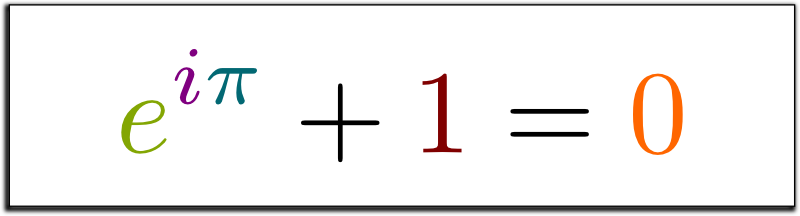


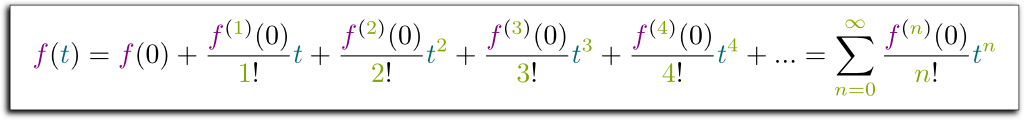
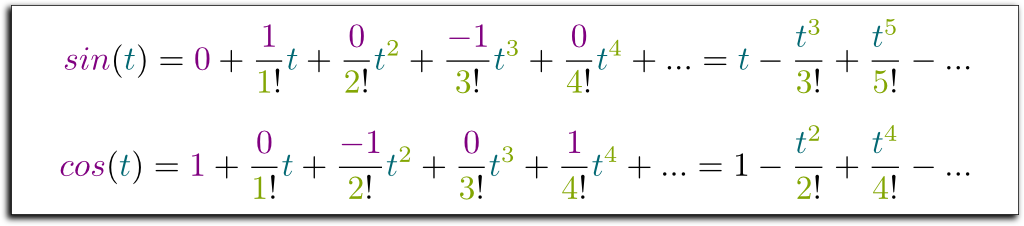
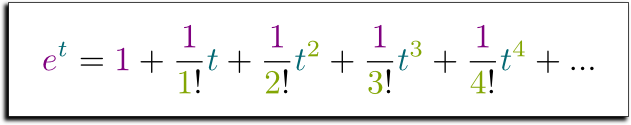
Leave a Reply