My parents always taught me to share, and I guess I did not always loved them for that when I was young and playing alone at Zelda, Ocarina of Time with my cousin next to me.
Sharing is a hard thing to do. Just look at the geopolitical tensions water sharing causes between India and Pakistan despite the Indus Water Treaty or the threats of a global war over water by 2030. And sharing is an everyday problem, whether it’s about the soccer field (please let me play ), the lunch table of the university cafeteria (I’m a graduate now, but still cannot get a table!) or the cheesecake stolen by Chandler Bing and Rachel Green.
Well… Yes, there is a very interesting theory on fair division. It all starts with the following example introduced by Steinhaus in 1948.
Two questions have to be raised: the definition of fairness and the way we can guarantee a fair division. In this article, we will only focus on the first question. The second part is dealt with in my article on mechanism design.
The literature gives several definitions of fairness in sharing problems. You can find them on wikipedia. Let’s start with the one most of us would come up with first.
Equitable division
A division is equitable if everyone has the same satisfaction level. This concept seems simple but it is not!
Comparing the satisfaction levels of different players with different preferences is a difficult problem which is definitely not solved by the definition given on this wikipedia page (the whole cake is worth 1 for everyone). Let’s see why on the following example.
Suppose four persons want to share a sugar cake with a cherry on top (in French, “la cerise sur le gateau” means the greatest of the great). Yet, three of them are on a diet and they only want the cherry. Assume that the last one hates cherries and is very hungry. I guess that the right thing to do would be to split the cherry in three equal parts, each for one of the first three persons, and to give the last part to the last person. And I think we can all agree that that’d be fair, right?
Yet, if we evaluate each person’s satisfaction according to the wikipedia definition, three of them would end up with a satisfaction of 1/3 and one of them would end up with 1. Thus, this is not an equitable division, although we’d all say that it’s a fair division!
Comparing different persons’ levels of satisfaction is very difficult. It’s one of the main problem I face in my PhD research. I’ll get to that in another post (wow, there are a lot of posts I am going to have to write!). But the literature has found other ways to define fairness. Let’s see them.
Proportional fairness
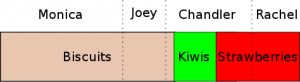
Let’s consider the following division of the cake:
This division is proportionally fair as each person gets a share that he considers is at least 1/4 of the whole cake. Monica and Chandler have large shares but they are not what they really wanted. On the opposite, Joey and Rachel have small shares of what they really wanted. Overall, they all value their shares.
Yes, you are right. It would better. But we are here working on fairness, not optimality (which I will probably talk about in a future post). I will quickly discuss this matter at the very end of this post too.
This division is fair because each person prefers his share than trading it randomly with another person’s share. Even if Joey prefers Monica’s share he would trade randomly to avoid ending up with Rachel’s share. Of course, if Joey does not take time to think about the risks of trading, he may be willing to accept a random trade. As a result of this last remark, a stronger definition of fairness has been given.
Envy-freeness
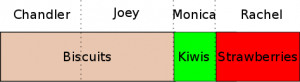
A division is envy-free if everyone prefers his own share to the others’. No one is jealous of any one else. No one would trade his share with any one else’s. For instance, the following division is envy-free.
Well, it’s a definition that many researchers use. Personally, I think it’s a pretty good definition because of its simplicity, although I think there is an even more precise (but more complex) definition, but I’ll get to that in another post. Nevertheless, this definition is interesting because it has many properties.
Well, the most interesting according to me is the following one. If the rules of the sharing process are the same for all persons and if all persons are smart, then the resulting division will be envy-free in means. As a matter of fact, if you are jealous of another person’s share, then you should have done what he had done.
One application of that is the first sentences of several constitutions:
-
“We hold these truths to be self-evident, that all men are created equal”, United States Declaration of Independence, Jefferson (1776).
-
“Les hommes naissent et demeurent libres et égaux en droits”, Déclaration des droits de l’homme et du citoyen(1789)
-
“All human beings are born free and equal in dignity and rights”, Universal Declaration of human rights (1948)
Unfortunately, you are right. Because rules are not the same for everyone, since some people get to grow up in families with more financial means, better education and great social networks (it’s not only about money, as opposed to what anti-heritage people would say!). But we can come up with a system even fairer…
Exact division
A division is exact if everyone values his share just as much as anyone else’s share. Hence, there is absolutely no point in sharing. Here’s how we can easily obtain such a division in the cake-cutting problem.
In this definition, equity means equality. Imagine the application of that in a society… Yes you get it! This leads to communism, in which all the goods are shared in the society with the same quantity of goods for everyone. Communism is the way to guarantee the best fairness (if not corrupted by a powerful government…)!
No, I am not. And I will give you a mathematical reason why I am not communist! The downside of this system is the non-optimality of the division (I told you I’d come back to that!). People would want to trade. Joey would trade his share of kiwis for Monica’s share of biscuits. Liberalization brings a better social surplus.
No, I am not either. When liberalizing a market, we give power to people to trade. If they behave honestly in a perfect competition, we would obtain both fairness and efficiency in our society. But no market is a perfect competition. And it’s not always in our best interest to behave honestly, which leads to imperfect competition with oligopolies (check out my post on electicity markets). Eventually, fairness is far from being guaranteed.
Well, that’s a very interesting thing, and there’s also a theory to take that into account, in the field of cooperative games. However, it assumes that there is a unique good that is valued the same way by everyone. The main contribution was brought by Nobel prize winner Lloyd Shapley in 1953, with the Shapley value.
Shapley value
In a cooperative game, players can collaborate or act on their owns. Now, if players do collaborate, then they’ll have to share their cumulated gains. The division of the cumulated gains needs to be done fairly. In particular, no player should feel so disappointed by his allocation that he’ll want to get out of the coalition.
Shapley came up with a way of dividing the cumulated gains in such a case, called the Shapley value. Basically, the more someone brings to coalitions he’s in, the more he should get out of the division of the cumulated gains. That’s sort of a meritocracy system.
OK, but it’s going to get a little technical. Let’s randomly permute the order of the players. Have each player enter the coalition in the generated order. Whenever a player enters the coalition, he increases the cumulated gain of the coalition. That’s what he will eventually be given. Now, repeat that with random permutations of players. Eventually, the means of allocations to each player is the Shapley value. Basically, it’s the means of what he adds to coalitions.
Of course not. He also came up with its properties. First, the Shapley value leads to an efficient division, since it divides all the cumulated gains. Second, it’s a symmetric division, which means that if two players have the exact same contributions, they’ll have the same allocations. Third, it’s a zero player allocation, as a player that never adds anything to coalitions is eventually given nothing. Finally, it’s an additive division. If we had two goods to divide, using the Shapley value for the sum of the two goods or using the Shapley values for each of the goods is equivalent.
I see three problems with the Shapley value. First, evaluating the Shapley value takes too much time. As a matter of fact, we should evaluate every permutation of players. For 10 players, there are already [math]10! = 3,628,800[/math] of them. For 20 players, there are [math]20! \approx 10^{20}[/math], which is way too many already for computation.
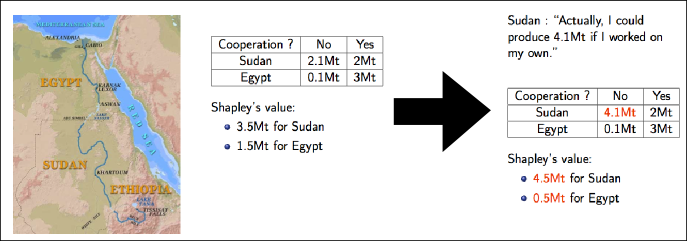
Second, and that’s even worse, in order to apply the Shapley value, we need to know what everyone brings to any coalition. Yet, for instance, if people collaborate, we can never observe what happens without the collaboration. We could ask players to tell us what they can do on their owns, but they’d have incentives to lie: that would be a bad mechanism design. The following example shows how countries using the Shapley value for cooperation over water-sharing can take advantage of lying about their abilities to produce food.
There are two orderings of the 2 countries, either Egypt first or Sudan first. For Egypt first, the production after Sudan entered is 5Mt, while the production before Sudan entered was Egypt’s production, that is .1Mt. Therefore, Sudan will be adding 5-.1=4.9Mt to the coalition. For Sudan first, Sudan will be adding its production to 0, that is 2.1Mt. The means of the contribution of Sudan is (4.9+2.1)/2=7/2=3.5Mt. It’s also its Shapley value.
Yes. The Shapley value does not guarantee to each player that he does not have incentives to get out of the coalition. It’s also possible that a subset of players have incentives to break the coalition and work on their owns. For that reason, the concept of the core has been invented.
The core is the set of divisions so that no subset of players has incentives to break the coalition. If we find a division of the core, then it will be fair, in the sense that nobody would complain and break the coalition. The core really is a stability concept. The problem with the core is that evaluating a division of the core is quite difficult. What’s more, the core may even be empty, which means that there is no way of making everyone collaborate for sure.
The research on cooperative games and finding ways to divide the cumulated gains is very active. But it’s a very open problem, especially in particular cases in which computation can be more easily done. But as I said for the Shapley value, a major problem of analyzes of cooperative games is the fact that we may not know what would have happened without cooperation. Other concepts in this field include the kernel and the nucleolus. But I’m not going to get into that.
Let’s sum up
Fairness is a difficult concept, and I can tell you that the definitions used in mathematics so far are not all good (that is why I can do a part of my PhD on the topic!). If there is one concept you should get out of that, it’s the envy-freeness. I think it’s the most realistic and the easiest to use or apply because of its properties. If you have goods to divide, make sure no one can say: “Hey that’s not fair, look at what you gave to that guy! I want that!” And they’ll all be happy with their shares. Of course, if a problem of meritocracy is raised, this concept cannot be applied, in which case, we should be thinking in terms of cooperative games.
I’d like to raise an important point. The major assumption we need to do to apply what we’ve seen is that the goods are tradable. It needs to make sense to say: “Let’s compare what I have with what others have”. Not all fairness problems can be modeled with this sentence. For instance, how do we compare the satisfaction of ecologists and nuclear companies, when a government announces he’ll divide the output of nuclear plants by two? This leads us to a moral question. It’s interesting to notice that fairness in a democracy is naturally defined by what the median person thinks. In fact, the concepts we have defined here are very hard to apply in macroeconomy. Yet, comparing standard of living in different societies is highly investigated. The most common way is by using the Human Development Index (HDI).
Finally (I am going to get out of topic…), I’d like to add that another important result we can get out of these analyzes is the importance of the diversity in tastes. In our example, we could really satisfy everyone because their tastes were very different. If they all only wanted kiwis, then they would have ended up more disappointed. In real life, some people are proud with their academic diplomas, where as others love playing in their bands and others simply enjoy their families. I believe that the diversification of points of interest is crucial to global happiness, especially in a world in which competition increases.