Tag Archives: Mathematics
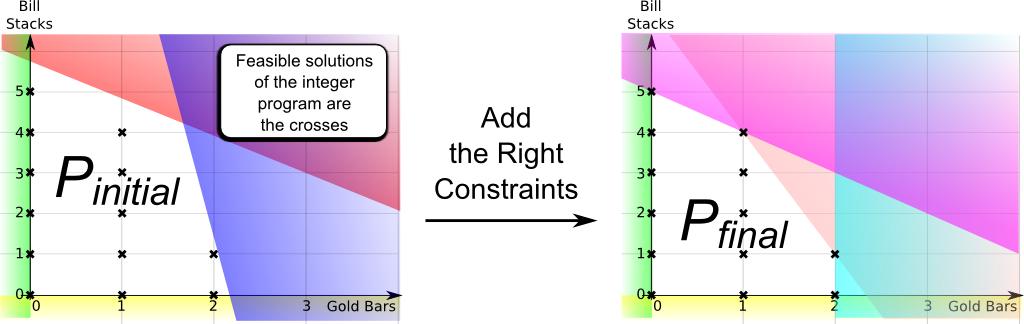
Optimization by Integer Programming
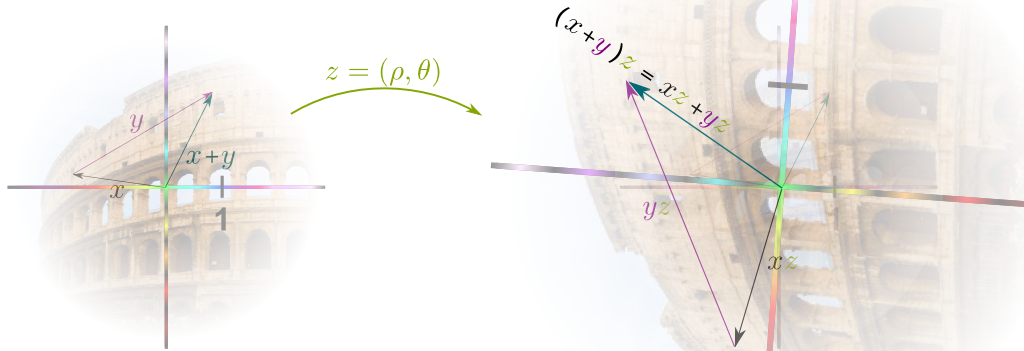
Imaginary and Complex Numbers
The Beauty of Ellipses, Parabolas and Hyperbolas

The Surprising Flavor of Infinite Series
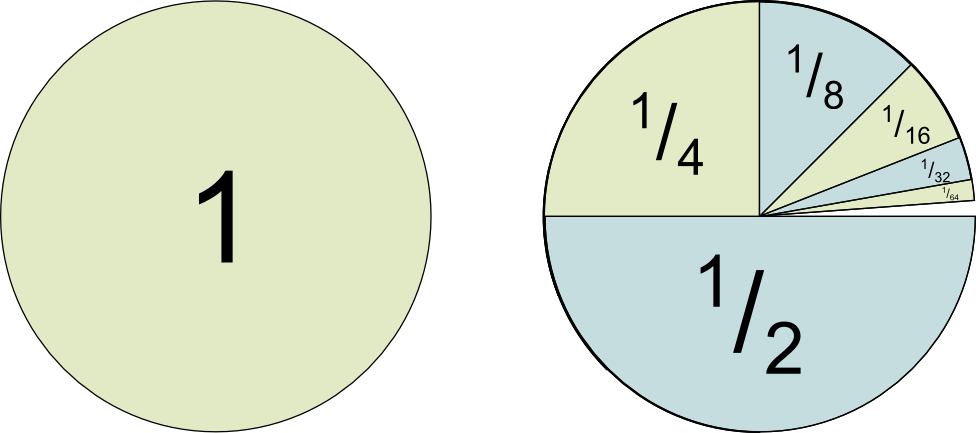
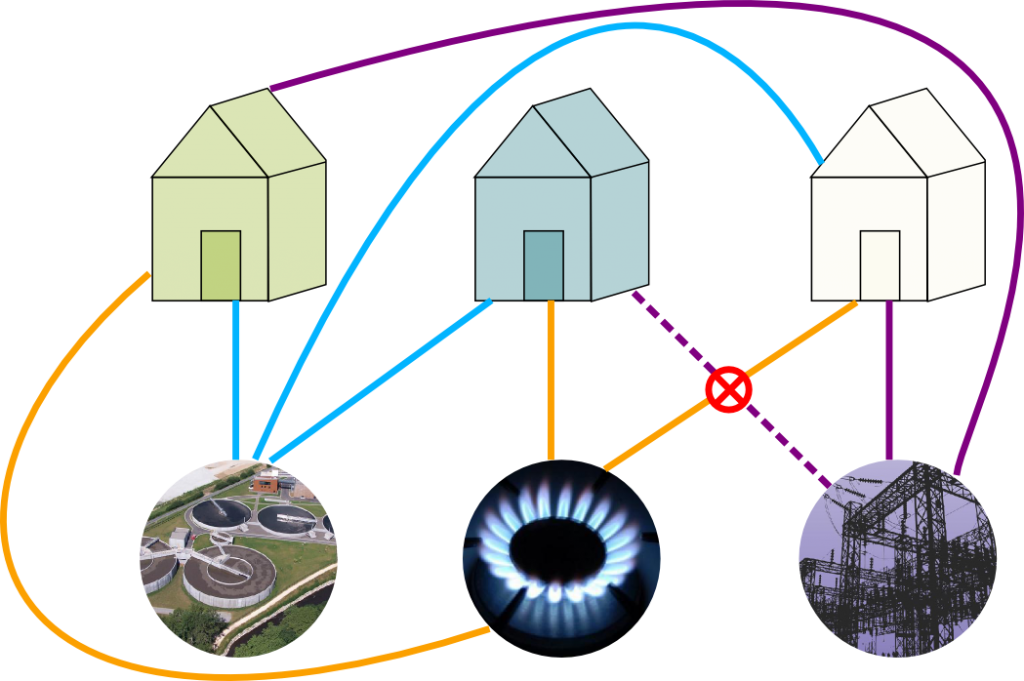
Euler’s Formula and the Utilities Problem
Proof by Mathematical Induction

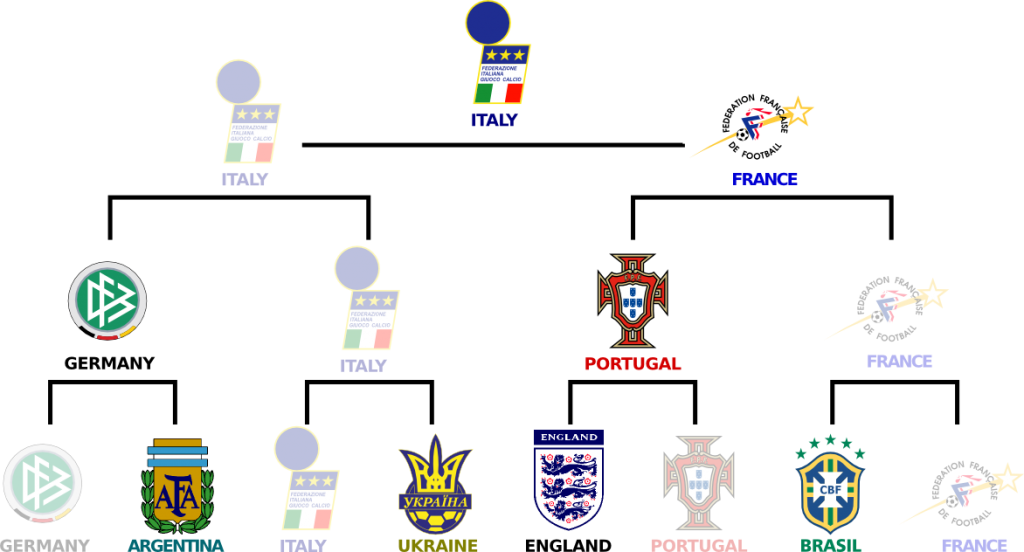
A Model of Football Games
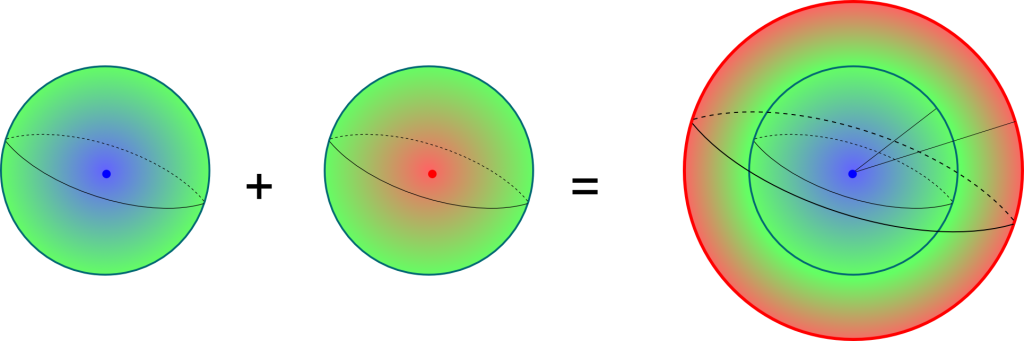
Poincaré Conjecture and Homotopy
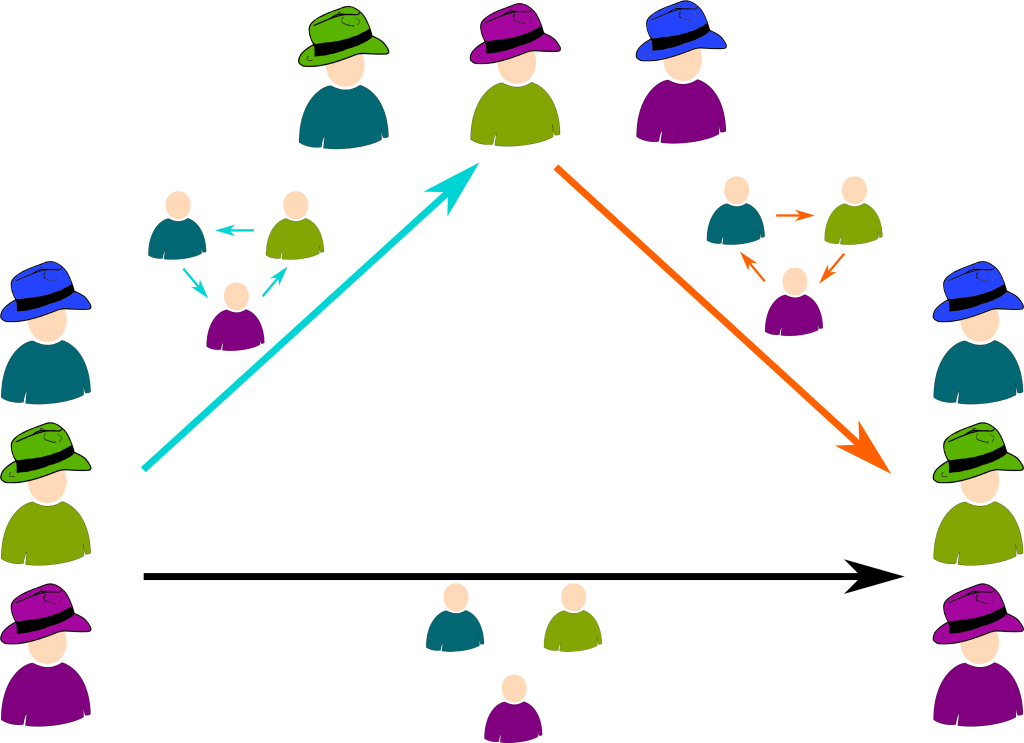
Shannon’s Information Theory

Space Deformation and Group Representation
Topology: from the Basics to Connectedness
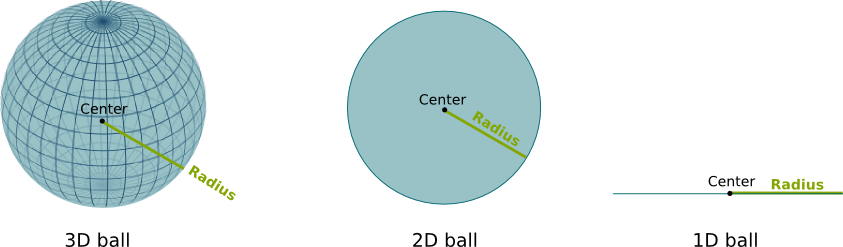
Construction and Definition of Numbers
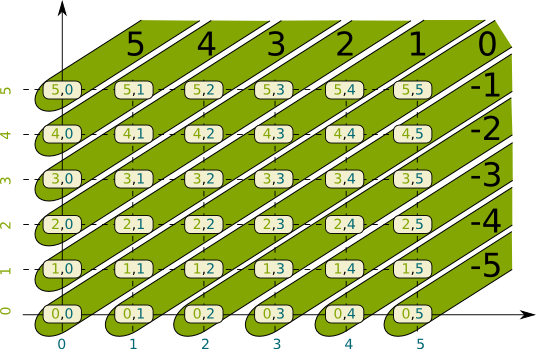
Self-Reference, Math Foundations and Gödel’s Incompleteness

Differential Calculus and the Geometry of Derivatives
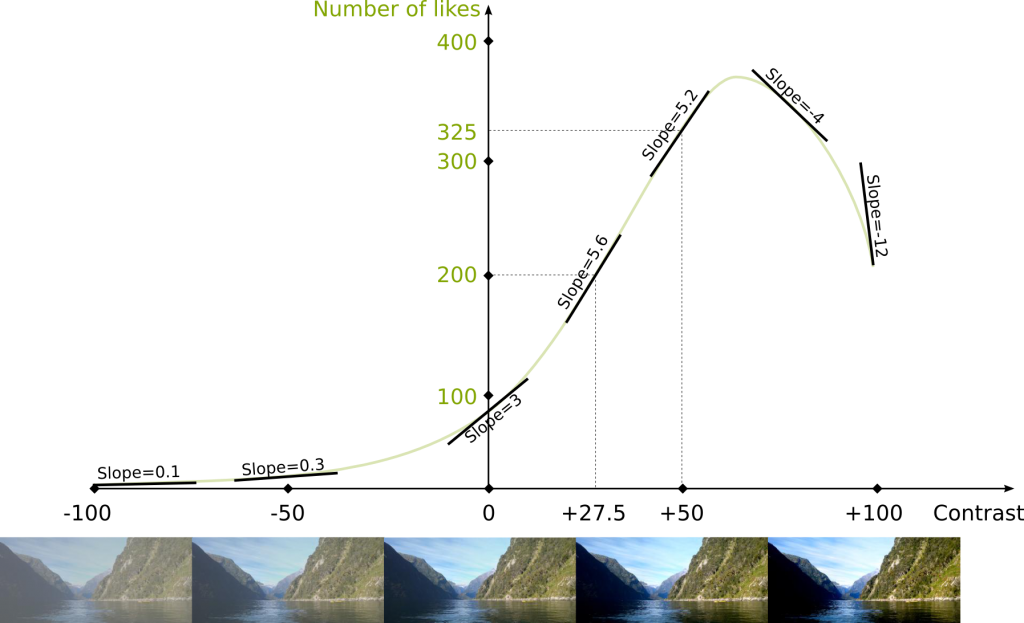
Bayesian Games: Math Models for Poker

Symmetries and Group Theory

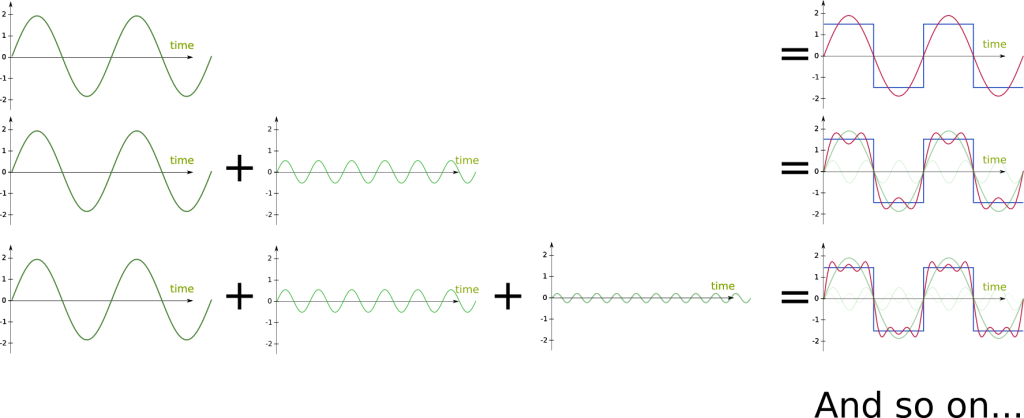
Fourier Analysis: Signals and Frequencies
Multicriteria with MACBETH

Advanced Game Theory Overview

Game Theory and the Nash Equilibrium